Hostname: page-component-76fb5796d-x4r87 Total loading time: 0 Render date: 2024-04-25T09:52:44.628Z Has data issue: false hasContentIssue false
  • English
  • Français

SLIDE REDUCTION, SUCCESSIVE MINIMA AND SEVERAL APPLICATIONS

Part of: Geometry of numbers Additive number theory; partitions

Published online by Cambridge University Press:  30 April 2013

JIANWEI LI  and
WEI WEI
JIANWEI LI*
Affiliation:
Institute for Advanced Study, Tsinghua University, Beijing 100084, PR China email wei-wei08@mails.tsinghua.edu.cn
WEI WEI
Affiliation:
Institute for Advanced Study, Tsinghua University, Beijing 100084, PR China email wei-wei08@mails.tsinghua.edu.cn
*
✉lijianwei10@mails.tsinghua.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Gama and Nguyen [‘Finding short lattice vectors within Mordell’s inequality’, in: Proceedings of the 40th Annual ACM Symposium on Theory of Computing, New York, 2008, 257–278] have presented slide reduction which is currently the best SVP approximation algorithm in theory. In this paper, we prove the upper and lower bounds for the ratios 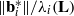$\Vert { \mathbf{b} }_{i}^{\ast } \Vert / {\lambda }_{i} (\mathbf{L} )$ and 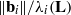$\Vert {\mathbf{b} }_{i} \Vert / {\lambda }_{i} (\mathbf{L} )$, where 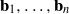${\mathbf{b} }_{1} , \ldots , {\mathbf{b} }_{n} $ is a slide reduced basis and 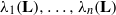${\lambda }_{1} (\mathbf{L} ), \ldots , {\lambda }_{n} (\mathbf{L} )$ denote the successive minima of the lattice 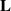$\mathbf{L} $. We define generalised slide reduction and use slide reduction to approximate 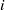$i$-SIVP, SMP and CVP. We also present a critical slide reduced basis for blocksize 2.

Keywords

slide reductionsuccessive minimaSIVPSMPCVP

MSC classification

Secondary: 11H06: Lattices and convex bodies 11P21: Lattice points in specified regions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 3 , December 2013 , pp. 390 - 406
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Ajtai, M., ‘Generating hard instances of lattice problems’, in: Complexity of Computations and Proofs, Vol. 13 of Quaderni di Matematica (ed. J. Krajicek), Seconda Universita di Napoli, 2004, 1–32.Google Scholar
Babai, L., ‘On Lovász’ lattice reduction and the nearest lattice point problem’, Combinatorica 6 (1986), 1–13.Google Scholar
Bachem, A. and Kannan, R., Lattices and the Basis Reduction Algorithm, TR (Carnegie Mellon University, 1984), 22–25.Google Scholar
Cohn, H. and Elkies, N., ‘New upper bounds on sphere packings I’, Ann. of Math. (2) 157 (2) (2003), 689–714.CrossRefGoogle Scholar
Conway, J. and Sloane, N., Sphere Packings, Lattices and Groups, 3rd edn (Springer, New York, 1998).Google Scholar
Gama, N., Howgrave-Graham, N., Koy, H. and Nguyen, P., ‘Rankin’s constant and blockwise lattice reduction’, in: Advances in Cryptology-Proceedings of CRYPTO’06, Lecture Notes in Computer Science, 4117 (Springer, New York, 2006), 112–130.Google Scholar
Gama, N., Howgrave-Graham, N. and Nguyen, P. Q., ‘Symplectic lattice reduction and NTRU’, in: Proceedings of EUROCRYPT’06, LNCS, 4004 (Springer, New York, 2006), 233–253.Google Scholar
Gama, N. and Nguyen, P. Q., ‘Finding short lattice vectors within Mordell’s inequality’, Proc. 40th Annual ACM Symposium on Theory of Computing, New York (2008), 207–216.Google Scholar
Kannan, R., ‘Minkowski’s convex body theorem and integer programming’, Math. Oper. Res. 12 (1987), 415–440.CrossRefGoogle Scholar
Korkine, A. and Zolotareff, G., ‘Sur les formes quadratiques’, Math. Ann. 6 (1873), 366–389.CrossRefGoogle Scholar
Lagarias, J. C., Lenstra, H. W. Jr and Schnorr, C. P., ‘Korkin-Zolotarev bases and successive minima of a lattice and its reciprocal lattice’, Combinatorica 10 (1990), 333–348.CrossRefGoogle Scholar
Lenstra, A. K., Lenstra, H. W. Jr and Lovász, L., ‘Factoring polynomials with rational coeffcients’, Math. Ann. 261 (1982), 515–534.Google Scholar
Mahler, K., ‘A theorem on inhomogeneous diophantine inequalities’, Nederl. Akad. Wetensch. 41 (1938), 634–637.Google Scholar
Martinet, J., Les réseaux parfaits des espaces euclidiens (Masson, Paris, 1996).Google Scholar
Micciancio, D., ‘How many LLL reduced bases are there? Answer 1’, http://mathoverflow.net/questions/57021 (7 June 2011).Google Scholar
Micciancio, D. and Regev, O., ‘Worst-case to average-case reductions based on Gaussian measures’, SIAM J. Comput. 37 (1) (2007), 267–302.CrossRefGoogle Scholar
Milnor, J. and Husemoller, D., Symmetric Bilinear Forms (Springer, New York, 1973).CrossRefGoogle Scholar
Regev, O., ‘On lattices, learning with errors, random linear codes, and cryptography’, Proc. 37th Annual ACM Symposium on Theory of Computing, Baltimore, MD (2005), 84–93.Google Scholar
Schnorr, C. P., ‘A hierarchy of polynomial time lattice basis reduction algorithms’, Theoret. Comput. Sci. 53 (1987), 201–224.Google Scholar
Schnorr, C. P., ‘Block Korkin-Zolotarev bases and successive minima’, Combin. Probab. Comput. 3 (1994), 507–522.Google Scholar
Schnorr, C. P. and Euchner, M., ‘Lattice basis reduction: improved algorithms and solving subset sum problems’, in: Proceedings of Fundamentals of Computation Theory, FCT’91 (ed. Budach, L.) (Springer LNCS 529, 1991), 68–85.Google Scholar