Article contents
SINGULARITY OF ORIENTED GRAPHS FROM SEVERAL CLASSES
Published online by Cambridge University Press: 21 November 2019
Abstract
A digraph is called oriented if there is at most one arc between two distinct vertices. An oriented graph 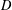 $D$ is nonsingular if its adjacency matrix
$D$ is nonsingular if its adjacency matrix 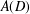 $A(D)$ is nonsingular. We characterise all nonsingular oriented graphs from three classes: graphs in which cycles are vertex disjoint, graphs in which all cycles share exactly one common vertex and graphs formed by cycles sharing a common path. As a straightforward corollary, the singularity of oriented bicyclic graphs is determined.
$A(D)$ is nonsingular. We characterise all nonsingular oriented graphs from three classes: graphs in which cycles are vertex disjoint, graphs in which all cycles share exactly one common vertex and graphs formed by cycles sharing a common path. As a straightforward corollary, the singularity of oriented bicyclic graphs is determined.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
Footnotes
Supported by National Natural Science Foundation of China (61702008, 11701008), Natural Science Foundation of Anhui Province (1808085MF193, 1808085QA04, 1908085QA31), Educational Commission of Anhui Province of China (KJ2018A0081) and Research Program of Outstanding Young Backbone Talents in Colleges and Universities of Anhui Province (GXGWFX2019015).
References
- 2
- Cited by



