Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-19T19:44:57.663Z Has data issue: false hasContentIssue false
  • English
  • Français

OVERPARTITIONS RELATED TO THE MOCK THETA FUNCTION 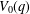$V_{0}(q)$

Part of: Combinatorics Additive number theory; partitions

Published online by Cambridge University Press:  16 January 2020

BERNARD L. S. LIN Open the ORCID record for BERNARD L. S. LIN [Opens in a new window]
BERNARD L. S. LIN*
Affiliation:
School of Science, Jimei University, Xiamen361021, PR China email linlsjmu@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Recently, Brietzke, Silva and Sellers [‘Congruences related to an eighth order mock theta function of Gordon and McIntosh’, J. Math. Anal. Appl.479 (2019), 62–89] studied the number 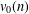$v_{0}(n)$ of overpartitions of $n$ into odd parts without gaps between the nonoverlined parts, whose generating function is related to the mock theta function 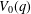$V_{0}(q)$ of order 8. In this paper we first present a short proof of the 3-dissection for the generating function of 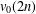$v_{0}(2n)$. Then we establish three congruences for 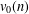$v_{0}(n)$ along certain progressions which are subsequences of the integers 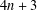$4n+3$.

Keywords

partitionoverpartition into odd partscongruencesmock theta function

MSC classification

Primary: 11P83: Partitions; congruences and congruential restrictions
Secondary: 05A17: Partitions of integers
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 3 , December 2020 , pp. 410 - 417
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by the National Natural Science Foundation of China (no. 11871246), the Natural Science Foundation of Fujian Province of China (no. 2019J01328) and the Program for New Century Excellent Talents in Fujian Province University (no. B17160).

References

Andrews, G. E., Dixit, A. and Yee, A. J., ‘Partitions associated with the Ramanujan/Watson mock theta functions 𝜔(q), 𝜈(q) and 𝜙(q)’, Res. Number Theory 1 (2015), article 19.CrossRefGoogle Scholar
Andrews, G. E., Hirschhorn, M. D. and Sellers, J. A., ‘Arithmetic properties of partitions with even parts distinct’, Ramanujan J. 23 (2010), 169–181.CrossRefGoogle Scholar
Andrews, G. E., Passary, D., Sellers, J. A. and Yee, A. J., ‘Congruences related to the Ramanujan/Watson mock theta functions 𝜔(q) and 𝜈(q)’, Ramanujan J. 43 (2017), 347–357.CrossRefGoogle Scholar
Berndt, B. C., Ramanujan’s Notebooks, Part III (Springer, New York, 1991).CrossRefGoogle Scholar
Berndt, B. C., Number Theory in the Spirit of Ramanujan (American Mathematical Society, Providence, RI, 2006).CrossRefGoogle Scholar
Brenti, F., ‘Determinants of super-Schur functions, lattice paths, and dotted plane partitions’, Adv. Math. 98 (1993), 27–64.CrossRefGoogle Scholar
Brietzke, E. H. M., Silva, R. and Sellers, J. A., ‘Congruences related to an eighth order mock theta function of Gordon and McIntosh’, J. Math. Anal. Appl. 479 (2019), 62–89.CrossRefGoogle Scholar
Bringmann, K. and Lovejoy, J., ‘Overpartitions and class numbers of binary quadratic forms’, Proc. Natl. Acad. Sci. USA 106 (2009), 5513–5516.CrossRefGoogle ScholarPubMed
Chan, S. H., ‘Congruences for Ramanujan’s 𝜙 function’, Acta Arith. 153 (2012), 161–189.CrossRefGoogle Scholar
Chan, S. H. and Mao, R., ‘Two congruences for Appell–Lerch sums’, Int. J. Number Theory 8(1) (2012), 111–123.CrossRefGoogle Scholar
Chen, W. Y. C. and Xia, E. X. W., ‘Proof of a conjecture of Hirschhorn and Sellers on overpartitions’, Acta Arith. 163 (2014), 59–69.CrossRefGoogle Scholar
Corteel, S. and Lovejoy, J., ‘Overpartitions’, Trans. Amer. Math. Soc. 356 (2004), 1623–1635.CrossRefGoogle Scholar
Dou, D. Q. J. and Lin, B. L. S., ‘New Ramanujan type congruences modulo 5 for overpartitions’, Ramanujan J. 44 (2017), 401–410.CrossRefGoogle Scholar
Hickerson, D. R. and Mortenson, E. T., ‘Hecke-type double sums, Appell–Lerch sums, and mock theta functions, I’, Proc. Lond. Math. Soc. 109 (2014), 382–422.CrossRefGoogle Scholar
Hirschhorn, M. D., The Power of q. A Personal Journey (Springer, Cham, 2017).CrossRefGoogle Scholar
Hirschhorn, M. D. and Sellers, J. A., ‘Arithmetic relations for overpartitions’, J. Combin. Math. Combin. Comput. 53 (2005), 65–73.Google Scholar
Kang, S.-J. and Kwon, J.-H., ‘Crystal bases of the Fock space representations and string functions’, J. Algebra 280 (2004), 313–349.CrossRefGoogle Scholar
Lebesgue, V. A., ‘Sommation de quelques series’, J. Math. Pures Appl. 5 (1840), 42–71.Google Scholar
Lovejoy, J., ‘Overpartitions and real quadratic fields’, J. Number Theory 106 (2004), 178–186.CrossRefGoogle Scholar
Mao, R., ‘Two identities on the mock theta function V 0(q)’, J. Math. Anal. Appl. 479 (2019), 122–134.CrossRefGoogle Scholar
McIntosh, R. J., ‘Second order mock theta functions’, Canad. Math. Bull. 50 (2007), 284–290.CrossRefGoogle Scholar
Wang, L., ‘New congruences for partitions related to mock theta functions’, J. Number Theory 175 (2017), 51–65.CrossRefGoogle Scholar