No CrossRef data available.
Article contents
A NOTE ON FREE ACTIONS OF GROUPS ON PRODUCTS OF SPHERES
Published online by Cambridge University Press: 08 March 2013
Abstract
It has been conjectured that if 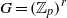 $G= \mathop{({ \mathbb{Z} }_{p} )}\nolimits ^{r} $ acts freely on a finite
$G= \mathop{({ \mathbb{Z} }_{p} )}\nolimits ^{r} $ acts freely on a finite 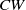 $CW$-complex
$CW$-complex 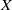 $X$ which is homotopy equivalent to a product of spheres
$X$ which is homotopy equivalent to a product of spheres 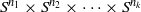 ${S}^{{n}_{1} } \times {S}^{{n}_{2} } \times \cdots \times {S}^{{n}_{k} } $, then
${S}^{{n}_{1} } \times {S}^{{n}_{2} } \times \cdots \times {S}^{{n}_{k} } $, then 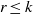 $r\leq k$. We address this question with the relaxation that
$r\leq k$. We address this question with the relaxation that 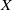 $X$ is finite-dimensional, and show that, to answer the question, it suffices to consider the case where the dimensions of the spheres are greater than or equal to
$X$ is finite-dimensional, and show that, to answer the question, it suffices to consider the case where the dimensions of the spheres are greater than or equal to 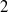 $2$.
$2$.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 88 , Issue 2 , October 2013 , pp. 340 - 344
- Copyright
- Copyright ©2013 Australian Mathematical Publishing Association Inc.


