No CrossRef data available.
Article contents
NEW SUPERCONGRUENCES INVOLVING PRODUCTS OF TWO BINOMIAL COEFFICIENTS
Published online by Cambridge University Press: 23 August 2019
Abstract
Let  $p>3$ be a prime and let
$p>3$ be a prime and let  $a$ be a rational
$a$ be a rational 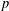 $p$-adic integer with
$p$-adic integer with 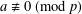 $a\not \equiv 0\;(\text{mod}\;p)$. We evaluate
$a\not \equiv 0\;(\text{mod}\;p)$. We evaluate 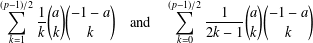 $$\begin{eqnarray}\mathop{\sum }_{k=1}^{(p-1)/2}\frac{1}{k}\binom{a}{k}\binom{-1-a}{k}\quad \text{and}\quad \mathop{\sum }_{k=0}^{(p-1)/2}\frac{1}{2k-1}\binom{a}{k}\binom{-1-a}{k}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{k=1}^{(p-1)/2}\frac{1}{k}\binom{a}{k}\binom{-1-a}{k}\quad \text{and}\quad \mathop{\sum }_{k=0}^{(p-1)/2}\frac{1}{2k-1}\binom{a}{k}\binom{-1-a}{k}\end{eqnarray}$$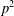 $p^{2}$ in terms of Bernoulli and Euler polynomials.
$p^{2}$ in terms of Bernoulli and Euler polynomials.
- Type
- Research Article
- Information
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
Footnotes
The author is supported by the National Natural Science Foundation of China (grant no. 11771173).


