Article contents
A NEW SUM–PRODUCT ESTIMATE IN PRIME FIELDS
Published online by Cambridge University Press: 24 May 2019
Abstract
We obtain a new sum–product estimate in prime fields for sets of large cardinality. In particular, we show that if 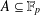 $A\subseteq \mathbb{F}_{p}$ satisfies
$A\subseteq \mathbb{F}_{p}$ satisfies 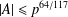 $|A|\leq p^{64/117}$ then
$|A|\leq p^{64/117}$ then 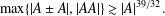 $\max \{|A\pm A|,|AA|\}\gtrsim |A|^{39/32}.$ Our argument builds on and improves some recent results of Shakan and Shkredov [‘Breaking the 6/5 threshold for sums and products modulo a prime’, Preprint, 2018, arXiv:1806.07091v1] which use the eigenvalue method to reduce to estimating a fourth moment energy and the additive energy
$\max \{|A\pm A|,|AA|\}\gtrsim |A|^{39/32}.$ Our argument builds on and improves some recent results of Shakan and Shkredov [‘Breaking the 6/5 threshold for sums and products modulo a prime’, Preprint, 2018, arXiv:1806.07091v1] which use the eigenvalue method to reduce to estimating a fourth moment energy and the additive energy 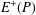 $E^{+}(P)$ of some subset
$E^{+}(P)$ of some subset 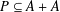 $P\subseteq A+A$. Our main novelty comes from reducing the estimation of
$P\subseteq A+A$. Our main novelty comes from reducing the estimation of 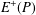 $E^{+}(P)$ to a point–plane incidence bound of Rudnev [‘On the number of incidences between points and planes in three dimensions’, Combinatorica 38(1) (2017), 219–254] rather than a point–line incidence bound used by Shakan and Shkredov.
$E^{+}(P)$ to a point–plane incidence bound of Rudnev [‘On the number of incidences between points and planes in three dimensions’, Combinatorica 38(1) (2017), 219–254] rather than a point–line incidence bound used by Shakan and Shkredov.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 100 , Issue 2 , October 2019 , pp. 268 - 280
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
Footnotes
The first and second author were supported by ARC Grant DP170100786.
References
- 1
- Cited by


