Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-24T07:36:19.181Z Has data issue: false hasContentIssue false
  • English
  • Français

NEAREST POINTS AND DELTA CONVEX FUNCTIONS IN BANACH SPACES

Part of: Approximations and expansions Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  03 September 2015

JONATHAN M. BORWEIN  and
OHAD GILADI
JONATHAN M. BORWEIN
Affiliation:
Centre for Computer-assisted Research Mathematics and its Applications (CARMA), School of Mathematical and Physical Sciences, University of Newcastle, Callaghan, NSW 2308, Australia email jonathan.borwein@newcastle.edu.au
OHAD GILADI*
Affiliation:
Centre for Computer-assisted Research Mathematics and its Applications (CARMA), School of Mathematical and Physical Sciences, University of Newcastle, Callaghan, NSW 2308, Australia email ohad.giladi@newcastle.edu.au
*
✉ohad.giladi@newcastle.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

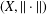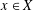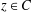Given a closed set $C$ in a Banach space $(X,\Vert \cdot \Vert )$, a point $x\in X$ is said to have a nearest point in $C$ if there exists $z\in C$ such that 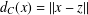$d_{C}(x)=\Vert x-z\Vert$, where 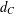$d_{C}$ is the distance of $x$ from 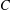$C$. We survey the problem of studying the size of the set of points in 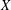$X$ which have nearest points in 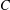$C$. We then turn to the topic of delta convex functions and indicate how it is related to finding nearest points.

Keywords

nearest pointsFréchet sub-differentialsdelta convex functions

MSC classification

Primary: 46B10: Duality and reflexivity
Secondary: 41A29: Approximation with constraints
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 93 , Issue 2 , April 2016 , pp. 283 - 294
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Araujo, A., ‘The nonexistence of smooth demand in general Banach spaces’, J. Math. Econom. 17(4) (1988), 309–319.Google Scholar
Bačák, M. and Borwein, J. M., ‘On difference convexity of locally Lipschitz functions’, Optimization 60(8–9) (2011), 961–978.Google Scholar
Borwein, J. M., ‘Proximality and Chebyshev sets’, Optim. Lett. 1(1) (2007), 21–32.Google Scholar
Borwein, J. M. and Fitzpatrick, S., ‘Existence of nearest points in Banach spaces’, Canad. J. Math. 41(4) (1989), 702–720.Google Scholar
Borwein, J. M. and Lewis, A. S., Convex Analysis and Nonlinear Optimization, 2nd edn, CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC, 3 (Springer, New York, 2006).Google Scholar
Borwein, J. M. and Preiss, D., ‘A smooth variational principle with applications to subdifferentiability and to differentiability of convex functions’, Trans. Amer. Math. Soc. 303(2) (1987), 517–527.CrossRefGoogle Scholar
Borwein, J. M. and Vanderwerff, J. D., Convex Functions: Constructions, Characterizations and Counterexamples, Encyclopedia of Mathematics and its Applications, 109 (Cambridge University Press, Cambridge, 2010).CrossRefGoogle Scholar
Borwein, J. M. and Zhu, Q. J., Techniques of Variational Analysis, CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC, 20 (Springer, New York, 2005).Google Scholar
Cepedello Boiso, M., ‘Approximation of Lipschitz functions by Δ-convex functions in Banach spaces’, Israel J. Math. 106 (1998), 269–284.Google Scholar
Cúth, M. and Rmoutil, M., ‘𝜎-porosity is separably determined’, Czechoslovak Math. J. 63(138)(1) (2013), 219–234.CrossRefGoogle Scholar
De Blasi, F. S., Myjak, J. and Papini, P. L., ‘Porous sets in best approximation theory’, J. Lond. Math. Soc. (2) 44(1) (1991), 135–142.CrossRefGoogle Scholar
Duda, J., ‘On inverses of 𝛿-convex mappings’, Comment. Math. Univ. Carolin. 42(2) (2001), 281–297.Google Scholar
Duda, J., ‘On the size of the set of points where the metric projection exists’, Israel J. Math. 140 (2004), 271–283.CrossRefGoogle Scholar
Duda, J., Veselý, L. and Zajíček, L., ‘On d.c. functions and mappings’, Atti Semin. Mat. Fis. Univ. Modena 51(1) (2003), 111–138.Google Scholar
Fabián, M., ‘Lipschitz smooth points of convex functions and isomorphic characterizations of Hilbert spaces’, Proc. Lond. Math. Soc. (3) 51(1) (1985), 113–126.CrossRefGoogle Scholar
Fabián, M. and Preiss, D., ‘On intermediate differentiability of Lipschitz functions on certain Banach spaces’, Proc. Amer. Math. Soc. 113(3) (1991), 733–740.Google Scholar
Fletcher, J. and Moors, W. B., ‘Chebyshev sets’, J. Aust. Math. Soc. 98(2) (2015), 161–231.CrossRefGoogle Scholar
Hartman, P., ‘On functions representable as a difference of convex functions’, Pacific J. Math. 9 (1959), 707–713.Google Scholar
Horst, R., Pardalos, P. M. and Thoai, N. V., Introduction to Global Optimization, 2nd edn, Nonconvex Optimization and its Applications, 48 (Kluwer Academic, Dordrecht, 2000).Google Scholar
Konjagin, S. V., ‘Approximation properties of closed sets in Banach spaces and the characterization of strongly convex spaces’, Dokl. Akad. Nauk SSSR 251(2) (1980), 276–280.Google Scholar
Kopecká, E. and Malý, J., ‘Remarks on delta-convex functions’, Comment. Math. Univ. Carolin. 31(3) (1990), 501–510.Google Scholar
Lau, K. S., ‘Almost Chebyshev subsets in reflexive Banach spaces’, Indiana Univ. Math. J. 27(5) (1978), 791–795.CrossRefGoogle Scholar
Lindenstrauss, J., Preiss, D. and Tišer, J., Fréchet Differentiability of Lipschitz Functions and Porous Sets in Banach Spaces, Annals of Mathematics Studies, 179 (Princeton University Press, Princeton, NJ, 2012).Google Scholar
Pavlica, D., ‘A d.c. C 1 function need not be difference of convex C 1 functions’, Comment. Math. Univ. Carolin. 46(1) (2005), 75–83.Google Scholar
Penot, J. P., Calculus without Derivatives, Graduate Texts in Mathematics, 266 (Springer, New York, 2013).Google Scholar
Preiss, D. and Zajíček, L., ‘Fréchet differentiation of convex functions in a Banach space with a separable dual’, Proc. Amer. Math. Soc. 91(2) (1984), 202–204.Google Scholar
Revalski, J. P. and Zhivkov, N. V., ‘Small sets in best approximation theory’, J. Global Optim. 50(1) (2011), 77–91.CrossRefGoogle Scholar
Revalski, J. P. and Zhivkov, N. V., ‘Best approximation problems in compactly uniformly rotund spaces’, J. Convex Anal. 19(4) (2012), 1153–1166.Google Scholar
Shalev-Shwartz, S., Online learning: Theory, algorithms, and applications, available at http://www.cs.huji.ac.il/ shais/papers/ShalevThesis07.pdf.Google Scholar
Stečkin, S. B., ‘Approximation properties of sets in normed linear spaces’, Rev. Math. Pures Appl. 8 (1963), 5–18.Google Scholar
Thach, P. T., ‘D.c. sets, d.c. functions and nonlinear equations’, Math. Program. 58(3, Ser. A) (1993), 415–428.Google Scholar
Thach, P. T. and Konno, H., ‘D.c. representability of closed sets in reflexive Banach spaces and applications to optimization problems’, J. Optim. Theory Appl. 91(1) (1996), 1–22.CrossRefGoogle Scholar
Veselý, L. and Zajíček, L., ‘Delta-convex mappings between Banach spaces and applications’, Dissertationes Math. (Rozprawy Mat.) 289 (1989), 52.Google Scholar
Veselý, L. and Zajíček, L., ‘On D.C. mappings and differences of convex operators’, Acta Univ. Carolin. Math. Phys. 42(2) (2001), 89–97; 29th Winter School on Abstract Analysis (Lhota nad Rohanovem/Zahrádky u České Lípy, 2001).Google Scholar
Zajíček, L., ‘Differentiability of the distance function and points of multivaluedness of the metric projection in Banach space’, Czechoslovak Math. J. 33(108)(2) (1983), 292–308.CrossRefGoogle Scholar
Zajíček, L., ‘On 𝜎-porous sets in abstract spaces’, Abstr. Appl. Anal. 5 (2005), 509–534.CrossRefGoogle Scholar