Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-25T15:28:36.823Z Has data issue: false hasContentIssue false
  • English
  • Français

LIPSCHITZ-TYPE INEQUALITIES FOR ANALYTIC FUNCTIONS IN BANACH ALGEBRAS

Part of: General theory of linear operators

Published online by Cambridge University Press:  11 April 2019

SILVESTRU SEVER DRAGOMIR Open the ORCID record for SILVESTRU SEVER DRAGOMIR [Opens in a new window]
SILVESTRU SEVER DRAGOMIR*
Affiliation:
Mathematics, College of Engineering and Science, Victoria University, PO Box 14428, Melbourne City, MC 8001, Australia DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences, School of Computer Science and Applied Mathematics, University of the Witwatersrand, Private Bag 3, Johannesburg 2050, South Africa email sever.dragomir@vu.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we provide some bounds for the quantity 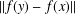$\Vert f(y)-f(x)\Vert$, where 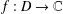$f:D\rightarrow \mathbb{C}$ is an analytic function on the domain 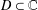$D\subset \mathbb{C}$ and $x$, 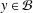$y\in {\mathcal{B}}$, a Banach algebra, with the spectra 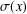$\unicode[STIX]{x1D70E}(x)$, 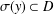$\unicode[STIX]{x1D70E}(y)\subset D$. Applications for the exponential and logarithmic functions on the Banach algebra 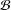${\mathcal{B}}$ are also given.

Keywords

Banach algebrasanalytic functionsLipschitz-type inequalitiesexponential and logarithmic functions on Banach algebra

MSC classification

Primary: 47A63: Operator inequalities
Secondary: 47A99: None of the above, but in this section
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 3 , December 2019 , pp. 489 - 497
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. and Stegun, I. A., Handbook of Mathematical Functions, National Bureau of Standards Applied Mathematics Series, 55 (US Government Printing Office, Washington, DC, 1972).Google Scholar
Bhatia, R., ‘First and second order perturbation bounds for the operator absolute value’, Linear Algebra Appl. 208–209 (1994), 367–376.Google Scholar
Bhatia, R., Matrix Analysis, Graduate Texts in Mathematics, 169 (Springer, New York, 1997).Google Scholar
Bhatia, R., Singh, D. and Sinha, K. B., ‘Differentiation of operator functions and perturbation bounds’, Comm. Math. Phys. 191(3) (1998), 603–611.Google Scholar
Boldea, M. V., Dragomir, S. S. and Megan, M., ‘New bounds for Čebyšev functional for power series in Banach algebras via a Grüss–Lupaş type inequality’, Panamer. Math. J. 26(3) (2016), 71–88.Google Scholar
Conway, J. B., A Course in Functional Analysis, 2nd edn (Springer, New York, 1990).Google Scholar
Douglas, R., Banach Algebra Techniques in Operator Theory, Graduate Texts in Mathematics, 179 (Springer, New York, 1998), originally published by Academic Press, 1972.Google Scholar
Dragomir, S. S., ‘Inequalities for power series in Banach algebras’, SUT J. Math. 50(1) (2014), 25–45.Google Scholar
Dragomir, S. S., ‘Inequalities of Lipschitz type for power series in Banach algebras’, Ann. Math. Sil. 29 (2015), 61–83.Google Scholar
Dragomir, S. S., Boldea, M. V., Buşe, C. and Megan, M., ‘Norm inequalities of Čebyšev type for power series in Banach algebras’, J. Inequal. Appl. 2014 (2014), Article ID 294, 19 pages.Google Scholar
Dragomir, S. S., Boldea, M. V. and Megan, M., ‘New norm inequalities of Čebyšev type for power series in Banach algebras’, Sarajevo J. Math. 11(24) (2015), 253–266.Google Scholar
Dragomir, S. S., Boldea, M. V. and Megan, M., ‘Further bounds for Čebyšev functional for power series in Banach algebras via Grüss–Lupaş type inequalities for p-norms’, Mem. Grad. Sch. Sci. Eng. Shimane Univ. Ser. B Math. 49 (2016), 15–34.Google Scholar
Dragomir, S. S., Boldea, M. V. and Megan, M., ‘Inequalities for Chebyshev functional in Banach algebras’, Cubo 19(1) (2017), 53–77.Google Scholar
Farforovskaya, Yu. B. and Nikolskaya, L., ‘Modulus of continuity of operator functions’, Algebra i Analiz 20(3) (2008), 224–242; translation in St. Petersburg Math. J. 20(3) (2009), 493–506.Google Scholar
Mikusiński, J., The Bochner Integral (Birkhäuser, Basel, 1978).Google Scholar
Rudin, W., Functional Analysis (McGraw Hill, New York, 1973).Google Scholar