Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-17T15:01:57.740Z Has data issue: false hasContentIssue false
  • English
  • Français

THE FINITE BASIS PROBLEM FOR THE MONOID OF TWO-BY-TWO UPPER TRIANGULAR TROPICAL MATRICES

Part of: Semigroups Model theory

Published online by Cambridge University Press:  08 January 2016

YUZHU CHEN ,
XUN HU ,
YANFENG LUO  and
OLGA SAPIR
YUZHU CHEN
Affiliation:
School of Mathematics and Statistics, Lanzhou University, Lanzhou, Gansu730000, PR China
XUN HU
Affiliation:
School of Mathematics and Statistics, Lanzhou University, Lanzhou, Gansu730000, PR China Department of Mathematics and Statistics, Chongqing Technology and Business University, Chongqing400033, PR China
YANFENG LUO*
Affiliation:
School of Mathematics and Statistics, Lanzhou University, Lanzhou, Gansu730000, PR China email luoyf@lzu.edu.cn
OLGA SAPIR
Affiliation:
Department of Mathematics, Vanderbilt University, Nashville, TN 37240, USA email olga.sapir@gmail.com
*
✉luoyf@lzu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For each positive $n$, let 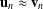$\mathbf{u}_{n}\approx \boldsymbol{v}_{n}$ denote the identity obtained from the Adjan identity 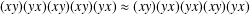$(xy)(yx)(xy)(xy)(yx)\approx (xy)(yx)(yx)(xy)(yx)$ by substituting 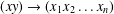$(xy)\rightarrow (x_{1}x_{2}\ldots x_{n})$ and 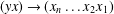$(yx)\rightarrow (x_{n}\ldots x_{2}x_{1})$. We show that every monoid which satisfies 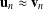$\mathbf{u}_{n}\approx \boldsymbol{v}_{n}$ for each positive $n$ and generates a variety containing the bicyclic monoid is nonfinitely based. This implies that the monoid 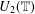$U_{2}(\mathbb{T})$ (respectively, 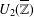$U_{2}(\overline{\mathbb{Z}})$) of two-by-two upper triangular tropical matrices over the tropical semiring 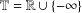$\mathbb{T}=\mathbb{R}\cup \{-\infty \}$ (respectively, 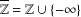$\overline{\mathbb{Z}}=\mathbb{Z}\cup \{-\infty \}$) is nonfinitely based.

Keywords

upper triangular tropical matricesidentitiesfinite basis problemnonfinitely basedbicyclic monoidAdjan identity

MSC classification

Primary: 20M07: Varieties and pseudovarieties of semigroups
Secondary: 03C05: Equational classes, universal algebra
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 1 , August 2016 , pp. 54 - 64
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Adjan, S. I., ‘Defining relations and algorithmic problems for groups and semigroups’, in: Proceeding of the Steklov Institute of Mathematics, 85 (American Mathematical Society, Providence, 1967).Google Scholar
Akian, M., Bapat, R. and Gaubert, S., ‘Max-plus algebra’, in: Handbook of Linear Algebra (eds. Hogben, L. et al. ) (Chapman and Hall, London, 2006).Google Scholar
Auinger, K., Chen, Y., Hu, X., Luo, Y. and Volkov, M. V., ‘The finite basis problem for Kauffman monoids’, Algebra Universalis 74 (2015), 333–350.CrossRefGoogle Scholar
Burris, S. and Sankappanavar, H. P., A Course in Universal Algebra (Springer, New York, 1981).Google Scholar
Butkovic̆, P., ‘Max-algebra: the linear algebra of combinatorics?’, Linear Algebra Appl. 367 (2003), 313–335.Google Scholar
Cohen, G., Gaubert, S. and Quadrat, J. P., ‘Max-plus algebra and system theory: where we are and where to go now’, Annu. Rev. Control 23 (1999), 207–219.Google Scholar
Cuninghame-Green, R., ‘Minimax algebra’, Lecture Notes in Econom. and Math. Systems 166 (1979), 1–258.CrossRefGoogle Scholar
Howie, J. M., Fundamentals of Semigroup Theory (Clarendon Press, Oxford, 1995).CrossRefGoogle Scholar
Izhakian, Z. and Margolis, S. W., ‘Semigroup identities in the monoid of two-by-two tropical matrices’, Semigroup Forum 80(2) (2010), 191–218.Google Scholar
Izhakian, Z., ‘Semigroup identities in the monoid of triangular tropical matrices’, Semigroup Forum 88(1) (2014), 145–161.CrossRefGoogle Scholar
Johnson, M. and Kambites, M., ‘Multiplicative structure of 2 × 2 tropical matrices’, Linear Algebra Appl. 435 (2011), 1612–1625.Google Scholar
Lee, E. W. H., ‘A sufficient condition for the non-finite basis property of semigroups’, Monatsh. Math. 168(3–4) (2012), 461–472.Google Scholar
Lee, E. W. H., Li, J. R. and Zhang, W. T., ‘Minimal non-finitely based semigroups’, Semigroup Forum 85(3) (2012), 577–580.Google Scholar
Li, J. R., Zhang, W. T. and Luo, Y. F., ‘On the finite basis problem for the variety generated by all n-element semigroups’, Algebra Universalis 73 (2015), 225–248.Google Scholar
Luo, Y. F. and Zhang, W. T., ‘On the variety generated by all semigroups of order three’, J. Algebra 334 (2011), 1–30.CrossRefGoogle Scholar
McKenzie, R., ‘Tarski’s finite basis problem is undecidable’, Internat. J. Algebra Comput. 6 (1996), 49–104.Google Scholar
Pachter, L. and Sturmfels, B., ‘Tropical geometry of statistical models’, Proc. Natl. Acad. Sci. USA 101(46) (2004), 16132–16137.Google Scholar
Pastijn, F., ‘Polyhedral convex cones and the equational theory of the bicyclic semigroup’, J. Aust. Math. Soc. 81 (2006), 63–96.CrossRefGoogle Scholar
Perkins, P., ‘Bases for equational theories of semigroups’, J. Algebra 11 (1969), 298–314.CrossRefGoogle Scholar
Sapir, M. V., ‘Problems of Burnside type and the finite basis property in varieties of semigroups’, Math. USSR Izv. 30(2) (1988), 295–314.Google Scholar
Sapir, O. B., ‘Non-finitely based monoids’, Semigroup Forum 90(3) (2015), 557–586.Google Scholar
Sapir, O. B., ‘Finitely based monoids’, Semigroup Forum 90(3) (2015), 587–614.Google Scholar
Shneerson, L. M., ‘On the axiomatic rank of varieties generated by a semigroup or monoid with one defining relation’, Semigroup Forum 39 (1989), 17–38.Google Scholar
Shleifer, F. G., ‘Looking for identities on a bicyclic semigroup with computer assistance’, Semigroup Forum 41 (1990), 173–179.Google Scholar
Shitov, Y., ‘Tropical matrices and group representations’, J. Algebra 370 (2012), 1–4.Google Scholar
Simon, I., ‘On semigroups of matrices over the tropical semiring’, RAIRO Theor. Inform. Appl. 28(3–4) (1994), 277–294.Google Scholar
Volkov, M. V., ‘The finite basis question for varieties of semigroups’, Math. Notes 45(3) (1989), 187–194; [translation of Mat. Zametki 45(3) (1989), 12–23].Google Scholar
Volkov, M. V., ‘The finite basis problem for finite semigroups’, Sci. Math. Jpn. 53 (2001), 171–199.Google Scholar
Zhang, W. T., Li, J. R. and Luo, Y. F., ‘On the variety generated by the monoid of triangular 2 × 2 matrices over a two-element field’, Bull. Aust. Math. Soc. 86(1) (2012), 64–77.CrossRefGoogle Scholar
Zhang, W. T., Li, J. R. and Luo, Y. F., ‘Hereditarily finitely based semigroups of triangular matrices over finite fields’, Semigroup Forum 86(2) (2013), 229–261.Google Scholar
Zhang, W. T. and Luo, Y. F., ‘A new example of non-finitely based semigroups’, Bull. Aust. Math. Soc. 84 (2011), 484–491.CrossRefGoogle Scholar