Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-16T21:44:27.282Z Has data issue: false hasContentIssue false
  • English
  • Français

THE FINITE BASIS PROBLEM FOR INVOLUTION SEMIGROUPS OF TRIANGULAR 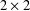$2\times 2$ MATRICES

Part of: Model theory Semigroups

Published online by Cambridge University Press:  02 October 2019

WEN TING ZHANG  and
YAN FENG LUO
WEN TING ZHANG*
Affiliation:
School of Mathematics and Statistics, Lanzhou University, Lanzhou, Gansu 730000, PR China Key Laboratory of Applied Mathematics and Complex Systems, Lanzhou, Gansu 730000, PR China email zhangwt@lzu.edu.cn
YAN FENG LUO
Affiliation:
School of Mathematics and Statistics, Lanzhou University, Lanzhou, Gansu 730000, PR China Key Laboratory of Applied Mathematics and Complex Systems, Lanzhou, Gansu 730000, PR China email luoyf@lzu.edu.cn
*
✉zhangwt@lzu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 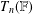$T_{n}(\mathbb{F})$ be the semigroup of all upper triangular 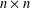$n\times n$ matrices over a field 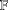$\mathbb{F}$. Let 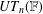$UT_{n}(\mathbb{F})$ and 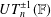$UT_{n}^{\pm 1}(\mathbb{F})$ be subsemigroups of 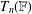$T_{n}(\mathbb{F})$, respectively, having 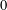$0$s and/or 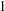$1$s on the main diagonal and 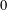$0$s and/or 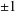$\pm 1$s on the main diagonal. We give some sufficient conditions under which an involution semigroup is nonfinitely based. As an application, we show that 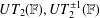$UT_{2}(\mathbb{F}),UT_{2}^{\pm 1}(\mathbb{F})$ and 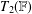$T_{2}(\mathbb{F})$ as involution semigroups under the skew transposition are nonfinitely based for any field 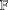$\mathbb{F}$.

Keywords

semigroupmatrixidentity basisfinite basis problemvariety

MSC classification

Primary: 20M05: Free semigroups, generators and relations, word problems
Secondary: 03C05: Equational classes, universal algebra
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 1 , February 2020 , pp. 88 - 104
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was partially supported by the National Natural Science Foundation of China (Nos. 11401275, 11771191 and 11371177) and the Fundamental Research Funds for the Central Universities (No. lzujbky-2016-96).

References

Almeida, J., Finite Semigroups and Universal Algebra (World Scientific, Singapore, 1994).Google Scholar
Auinger, K., Dolinka, I., Pervukhina, T. V. and Volkov, M. V., ‘Unary enhancements of inherently non-finitely based semigroups’, Semigroup Forum 89(1) (2014), 41–51.Google Scholar
Auinger, K., Dolinka, I. and Volkov, M. V., ‘Matrix identities involving multiplication and transposition’, J. Eur. Math. Soc. (JEMS) 14(3) (2012), 937–969.Google Scholar
Auinger, K., Dolinka, I. and Volkov, M. V., ‘Equational theories of semigroups with involution’, J. Algebra 369 (2012), 203–225.Google Scholar
Bahturin, Y. A. and Ol’shanskii, A. Y., ‘Identical relations in finite Lie rings’, Math. Sb. (N.S.) 96(138) (1975), 543–559; (in Russian); English translation, Math. USSR Sb. 25 (1975), 507–523.Google Scholar
Burris, S. and Sankappanavar, H. P., A Course in Universal Algebra (Springer, New York, 1981).Google Scholar
Chen, Y. Z., Hu, X. and Luo, Y. F., ‘On the finite basis problem for a certain semigroup of upper triangular matrices over a field’, J. Algebra Appl. 15 (2016), 1650177.Google Scholar
Crvenkoic, S., Dolinka, I. and Ésik, Z., ‘The variety of Kleene algebras with conversion is not finitely based’, Theoret. Comput. Sci. 230 (2000), 235–245.Google Scholar
Ježek, J., ‘Nonfinitely based three-element idempotent groupoids’, Algebra Universalis 20 (1985), 292–301.Google Scholar
Kruse, R., ‘Identities satisfied in a finite ring’, J. Algebra 26 (1973), 298–318.Google Scholar
Lee, E. W. H., ‘Finite involution semigroups with infinite irredundant bases of identities’, Forum Math. 28(3) (2016), 587–607.Google Scholar
Li, J. R. and Luo, Y. F., ‘On the finite basis problem for the monoids of triangular boolean matrices’, Algebra Universalis 65 (2011), 353–362.Google Scholar
L’vov, I. V., ‘Varieties of associative rings I’, Algebra Logika 12 (1973), 269–297.Google Scholar
McKenzie, R., ‘Equational bases for lattice theories’, Math. Scand. 27 (1970), 24–38.Google Scholar
McKenzie, R., ‘Tarski’s finite basis problem is undecidable’, Internat. J. Algebra Comput. 6 (1996), 49–104.Google Scholar
Murskiĭ, V. L., ‘The existence in the three-valued logic of a closed class with a finite basis having no finite complete system of identities’, Sov. Math. Dokl. 6 (1965), 1020–1024.Google Scholar
Oates, S. and Powell, M. B., ‘Identical relations in finite groups’, J. Algebra 1 (1964), 11–39.Google Scholar
Perkins, P., ‘Bases for equational theories of semigroups’, J. Algebra 11 (1969), 298–314.Google Scholar
Perkins, P., ‘Finite axiomatizability for equational theories of computable groupoids’, J. Symbolic Logic 54 (1989), 1018–1022.Google Scholar
Shevrin, L. N. and Volkov, M. V., ‘Identities of semigroups’, Izv. Vyssh. Uchebn. Zaved. Mat. 29(11) (1985), 3–47; (in Russian); English translation, Sov. Math. (Iz. VUZ) 29(11) (1985), 1–64.Google Scholar
Volkov, M. V., ‘The finite basis problem for finite semigroups’, Sci. Math. Jpn. 53 (2001), 171–199.Google Scholar
Volkov, M. V., ‘A nonfinitely based semigroup of triangular matrices’, in: Semigroups, Algebra and Operator Theory (eds. Meakin, J., Rajan, A. R. and Romeo, P. G.) (Springer, New Delhi–Heidelberg–New York–Dordrecht–London, 2015), 27–38.Google Scholar
Volkov, M. V. and Goldberg, I. A., ‘Identities of semigroups of triangular matrices over finite fields’, Math. Notes 73 (2003), 474–481; English translation of Mat. Zametki 73 (2003), 502–510.Google Scholar
Zhang, W. T., Ji, Y. D. and Luo, Y. F., ‘The finite basis problem for infinite involution semigroups of triangular 2 × 2 matrices’, Semigroup Forum 94 (2017), 426–441.Google Scholar
Zhang, W. T., Li, J. R. and Luo, Y. F., ‘On the variety generated by the monoid of triangular 2 × 2 matrices over a two-element field’, Bull. Aust. Math. Soc. 86(1) (2012), 64–77.Google Scholar
Zhang, W. T., Li, J. R. and Luo, Y. F., ‘Hereditarily finitely based semigroups of triangular matrices over the two-element field’, Semigroup Forum 86(2) (2013), 229–261.Google Scholar