Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-23T23:13:20.116Z Has data issue: false hasContentIssue false
  • English
  • Français

THE ESSENTIAL NORMS OF COMPOSITION OPERATORS ON WEIGHTED DIRICHLET SPACES

Part of: Special classes of linear operators

Published online by Cambridge University Press:  31 January 2018

YUFEI LI Open the ORCID record for YUFEI LI [Opens in a new window] ,
YUFENG LU Open the ORCID record for YUFENG LU [Opens in a new window]  and
TAO YU Open the ORCID record for TAO YU [Opens in a new window]
YUFEI LI*
Affiliation:
Department of Mathematical Sciences, Dalian University of Technology, Liaoning, Dalian, 116024, PR China email liyf495@mail.dlut.edu.cn
YUFENG LU
Affiliation:
Department of Mathematical Sciences, Dalian University of Technology, Liaoning, Dalian, 116024, PR China email lyfdlut@dlut.edu.cn
TAO YU
Affiliation:
Department of Mathematical Sciences, Dalian University of Technology, Liaoning, Dalian, 116024, PR China email tyu@dlut.edu.cn
*
✉liyf495@mail.dlut.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 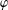$\unicode[STIX]{x1D711}$ be an analytic self-map of the unit disc. If 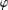$\unicode[STIX]{x1D711}$ is analytic in a neighbourhood of the closed unit disc, we give a precise formula for the essential norm of the composition operator 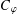$C_{\unicode[STIX]{x1D711}}$ on the weighted Dirichlet spaces 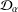${\mathcal{D}}_{\unicode[STIX]{x1D6FC}}$ for 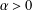$\unicode[STIX]{x1D6FC}>0$. We also show that, for a univalent analytic self-map 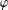$\unicode[STIX]{x1D711}$ of 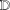$\mathbb{D}$, if 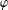$\unicode[STIX]{x1D711}$ has an angular derivative at some point of 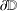$\unicode[STIX]{x2202}\mathbb{D}$, then the essential norm of 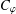$C_{\unicode[STIX]{x1D711}}$ on the Dirichlet space is equal to one.

Keywords

weighted Dirichlet spacecomposition operatorgeneralised Nevanlinna counting functionessential normangular derivative

MSC classification

Primary: 47B33: Composition operators
Secondary: 47B38: Operators on function spaces (general)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 2 , April 2018 , pp. 297 - 307
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

This research is supported by NSFC grant no. 11671065. The third author is supported by the NSFC grant nos. 11271332 and 11431011.

References

Carswell, B. and Hammond, C., ‘Composition operators with maximal norm on weighted Bergman spaces’, Proc. Amer. Math. Soc. 134 (2006), 2599–2605.CrossRefGoogle Scholar
Cima, J. A. and Matheson, A. L., ‘Essential norms of composition operators and Aleksandrov measures’, Pacific J. Math. 179 (1997), 59–64.Google Scholar
Cowen, C. C., ‘Composition operators on H 2 ’, J. Operator Theory 9 (1983), 77–106.Google Scholar
Cowen, C. C. and MacCluer, B. D., Composition Operators on Spaces of Analytic Functions (CRC Press, Boca Raton, 1995).Google Scholar
Garnett, J. B., Bounded Analytic Functions (Springer, New York, 2007).Google Scholar
Hammond, C., ‘The norm of a composition operator with linear symbol acting on the Dirichlet space’, J. Math. Anal. Appl. 303 (2005), 499–508.Google Scholar
MacCluer, B. D. and Shapiro, J. H., ‘Angular derivative and compact composition operators on the Hardy and Bergman spaces’, Canad. J. Math. 38 (1986), 878–906.Google Scholar
Poggi-Corradini, P., The Essential Norm of Composition Operators Revisited, Contemporary Mathematics, 213 (American Mathematical Society, Providence, RI, 1998), 167–173.Google Scholar
Shapiro, J. H., ‘The essential norm of a composition operator’, Ann. of Math. (2) 125(2) (1987), 375–404.CrossRefGoogle Scholar
Shapiro, J. H., Composition Operators and Classical Function Theory (Springer, New York, 1993).Google Scholar
Shimorin, S., ‘Factorization of analytic functions in weighted Bergman spaces’, St. Petersburg Math. J. 5 (1994), 1005–1022.Google Scholar
Shimorin, S., ‘On a family of conformally invariant operators’, St. Petersburg Math. J. 7 (1996), 287–306.Google Scholar
Shimorin, S., ‘The green function for the weighted biharmonic operator 𝛥(1 -|z|2)-𝛼𝛥, and factorization of analytic functions’, J. Math. Sci. 87 (1997), 3912–3924.Google Scholar
Zhu, K., Operator Theory in Function Spaces, 2nd edn (American Mathematical Society, Providence, RI, 2007).Google Scholar