We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
For every integer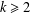 
$k\geq 2$
and every 
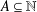$A\subseteq \mathbb{N}$
, we define the 
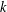$k$
-directions sets of 
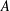$A$
as 
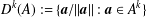$D^{k}(A):=\{\boldsymbol{a}/\Vert \boldsymbol{a}\Vert :\boldsymbol{a}\in A^{k}\}$
and 
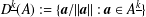$D^{\text{}\underline{k}}(A):=\{\boldsymbol{a}/\Vert \boldsymbol{a}\Vert :\boldsymbol{a}\in A^{\text{}\underline{k}}\}$
, where 
$\Vert \cdot \Vert$
is the Euclidean norm and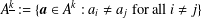 
$A^{\text{}\underline{k}}:=\{\boldsymbol{a}\in A^{k}:a_{i}\neq a_{j}\text{ for all }i\neq j\}$
. Via an appropriate homeomorphism, 
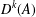$D^{k}(A)$
is a generalisation of the ratio set
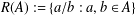$R(A):=\{a/b:a,b\in A\}$
. We study 
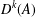$D^{k}(A)$
and 
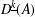$D^{\text{}\underline{k}}(A)$
as subspaces of 
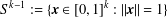$S^{k-1}:=\{\boldsymbol{x}\in [0,1]^{k}:\Vert \boldsymbol{x}\Vert =1\}$
. In particular, generalising a result of Bukor and Tóth, we provide a characterisation of the sets 
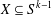$X\subseteq S^{k-1}$
such that there exists 
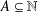$A\subseteq \mathbb{N}$
satisfying 
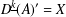$D^{\text{}\underline{k}}(A)^{\prime }=X$
, where 
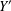$Y^{\prime }$
denotes the set of accumulation points of 
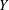$Y$
. Moreover, we provide a simple sufficient condition for 
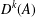$D^{k}(A)$
to be dense in 
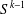$S^{k-1}$
. We conclude with questions for further research.
