Article contents
COMMON SLOTS OF BILINEAR AND QUADRATIC PFISTER FORMS
Published online by Cambridge University Press: 03 May 2018
Abstract
We show that over any field 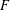 $F$ of characteristic 2 and 2-rank
$F$ of characteristic 2 and 2-rank  $n$, there exist
$n$, there exist 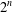 $2^{n}$ bilinear
$2^{n}$ bilinear  $n$-fold Pfister forms that have no slot in common. This answers a question of Becher [‘Triple linkage’, Ann.
$n$-fold Pfister forms that have no slot in common. This answers a question of Becher [‘Triple linkage’, Ann.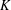 $K$-Theory, to appear] in the negative. We provide an analogous result also for quadratic Pfister forms.
$K$-Theory, to appear] in the negative. We provide an analogous result also for quadratic Pfister forms.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
References
- 2
- Cited by


