Article contents
APPLICATIONS OF LERCH’S THEOREM TO PERMUTATIONS OF QUADRATIC RESIDUES
Published online by Cambridge University Press: 10 July 2019
Abstract
Let  $n$ be a positive integer and
$n$ be a positive integer and  $a$ an integer prime to
$a$ an integer prime to  $n$. Multiplication by
$n$. Multiplication by  $a$ induces a permutation over
$a$ induces a permutation over 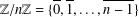 $\mathbb{Z}/n\mathbb{Z}=\{\overline{0},\overline{1},\ldots ,\overline{n-1}\}$. Lerch’s theorem gives the sign of this permutation. We explore some applications of Lerch’s result to permutation problems involving quadratic residues modulo
$\mathbb{Z}/n\mathbb{Z}=\{\overline{0},\overline{1},\ldots ,\overline{n-1}\}$. Lerch’s theorem gives the sign of this permutation. We explore some applications of Lerch’s result to permutation problems involving quadratic residues modulo  $p$ and confirm some conjectures posed by Sun [‘Quadratic residues and related permutations and identities’, Preprint, 2018, arXiv:1809.07766]. We also study permutations involving arbitrary
$p$ and confirm some conjectures posed by Sun [‘Quadratic residues and related permutations and identities’, Preprint, 2018, arXiv:1809.07766]. We also study permutations involving arbitrary 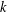 $k$th power residues modulo
$k$th power residues modulo 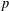 $p$ and primitive roots modulo a power of
$p$ and primitive roots modulo a power of 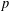 $p$.
$p$.
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 100 , Issue 3 , December 2019 , pp. 362 - 371
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
Footnotes
This research was supported by the National Natural Science Foundation of China (grant no. 11571162).
References
- 2
- Cited by


