No CrossRef data available.
Article contents
THE ANNIHILATOR OF TENSOR SPACE IN THE 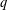 $q$-ROOK MONOID ALGEBRA
$q$-ROOK MONOID ALGEBRA
Published online by Cambridge University Press: 02 March 2017
Abstract
In this paper, we give an explicit construction of a quasi-idempotent in the 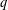 $q$-rook monoid algebra
$q$-rook monoid algebra 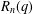 $R_{n}(q)$ and show that it generates the whole annihilator of the tensor space
$R_{n}(q)$ and show that it generates the whole annihilator of the tensor space 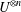 $U^{\otimes n}$ in
$U^{\otimes n}$ in 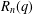 $R_{n}(q)$.
$R_{n}(q)$.
- Type
- Research Article
- Information
- Copyright
- © 2017 Australian Mathematical Publishing Association Inc.


