No CrossRef data available.
Article contents
PARTITIONS OF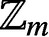 
$\mathbb {Z}_m$ WITH IDENTICAL REPRESENTATION FUNCTION
Part of:
Sequences and sets
Published online by Cambridge University Press: 22 September 2020
Abstract
For a given set
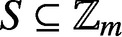$S\subseteq \mathbb {Z}_m$
and
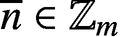$\overline {n}\in \mathbb {Z}_m$
, let
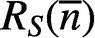$R_S(\overline {n})$
denote the number of solutions of the equation
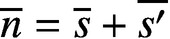$\overline {n}=\overline {s}+\overline {s'}$
with ordered pairs
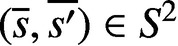$(\overline {s},\overline {s'})\in S^2$
. We determine the structure of
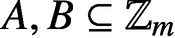$A,B\subseteq \mathbb {Z}_m$
with
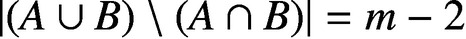$|(A\cup B)\setminus (A\cap B)|=m-2$
such that
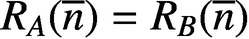$R_{A}(\overline {n})=R_{B}(\overline {n})$
for all
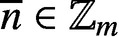$\overline {n}\in \mathbb {Z}_m$
, where m is an even integer.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2020 Australian Mathematical Publishing Association Inc.
Footnotes
This work was supported by the National Natural Science Foundation of China, Grant No. 11771211. The first author is also supported by the Project of Graduate Education Innovation of Jiangsu Province, Grant No. KYCX20_1167.
References
Chen, Y. G. and Lev, V. F., ‘Integer sets with identical representation functions’, Integers 16 (2016), Article ID A36, 4 pages.Google Scholar
Chen, Y. G. and Tang, M., ‘Partitions of natural numbers with the same representation functions’, J. Number Theory 129 (2009), 2689–2695.CrossRefGoogle Scholar
Dombi, G., ‘Additive properties of certain sets’, Acta Arith. 103 (2002), 137–146.CrossRefGoogle Scholar
Kiss, S. Z. and Sándor, C., ‘Partitions of the set of nonnegative integers with the same representation functions’, Discrete Math. 340 (2017), 1154–1161.CrossRefGoogle Scholar
Lev, V. F., ‘Reconstructing integer sets from their representation functions’, Electron. J. Combin. 11 (2004), Article ID R78, 6 pages.CrossRefGoogle Scholar
Li, J. W. and Tang, M., ‘Partitions of the set of nonnegative integers with the same representation functions’, Bull. Aust. Math. Soc. 97 (2018), 200–206.CrossRefGoogle Scholar
Sándor, C., ‘Partitions of natural numbers and their representation functions’, Integers 4 (2004), Article ID A18, 5 pages.Google Scholar
Tang, M., ‘Partitions of the set of natural numbers and their representation functions’, Discrete Math. 308 (2008), 2614–2616.CrossRefGoogle Scholar
Tang, M., ‘Partitions of natural numbers and their representation functions’, Chinese Ann. Math. Ser A 37 (2016), 41–46; English translation, Chinese J. Contemp. Math. 37 (2016), 39–44.Google Scholar
Yang, Q. H. and Chen, F. J. ‘Partitions of 
${\mathbb{Z}}_m$with the same representation functions’, Austral. J. Combin. 53 (2012), 257–262.Google Scholar
${\mathbb{Z}}_m$with the same representation functions’, Austral. J. Combin. 53 (2012), 257–262.Google ScholarYang, Q. H. and Tang, M., ‘Representation functions on finite sets with extreme symmetric differences’, J. Number Theory 180 (2017), 73–85.CrossRefGoogle Scholar