Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
Hostname: page-component-768dbb666b-6zkrn Total loading time: 1.228 Render date: 2023-02-05T15:27:59.375Z Has data issue: true Feature Flags: { "useRatesEcommerce": false } hasContentIssue true
  • English
Bulletin of the Australian Mathematical Society Bulletin of the Australian Mathematical Society

Article contents

NOTES ON ATKIN–LEHNER THEORY FOR DRINFELD MODULAR FORMS

Part of: Arithmetic algebraic geometry Discontinuous groups and automorphic forms Topological fields

Published online by Cambridge University Press:  15 November 2022

TARUN DALAL Open the ORCID record for TARUN DALAL[Opens in a new window]  and
NARASIMHA KUMAR Open the ORCID record for NARASIMHA KUMAR[Opens in a new window]
TARUN DALAL
Affiliation:
Department of Mathematics, Indian Institute of Technology Hyderabad, Kandi, Sangareddy 502285, India e-mail: ma17resch11005@iith.ac.in
NARASIMHA KUMAR*
Affiliation:
Department of Mathematics, Indian Institute of Technology Hyderabad, Kandi, Sangareddy 502285, India
*
e-mail: narasimha@math.iith.ac.in
Get access Rights & Permissions[Opens in a new window]

Abstract

We settle a part of the conjecture by Bandini and Valentino [‘On the structure and slopes of Drinfeld cusp forms’, Exp. Math.31(2) (2022), 637–651] for 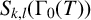$S_{k,l}(\Gamma _0(T))$ when 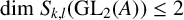$\mathrm {dim}\ S_{k,l}(\mathrm {GL}_2(A))\leq 2$ . We frame and check the conjecture for primes 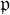$\mathfrak {p}$ and higher levels 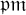$\mathfrak {p}\mathfrak {m}$ , and show that a part of the conjecture for level 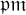$\mathfrak {p} \mathfrak {m}$ does not hold if 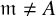$\mathfrak {m}\ne A$ and 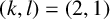$(k,l)=(2,1)$ .

Keywords

Drinfeld cusp formsoldformsnewformsAtkin–Lehner operatorsHecke operatorscommutativitydiagonalisability

MSC classification

Primary: 11F52: Modular forms associated to Drinfel'd modules
Secondary: 11F25: Hecke-Petersson operators, differential operators (one variable) 11G09: Drinfel'd modules; higher-dimensional motives, etc. 12J25: Non-Archimedean valued fields
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 19
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author thanks University Grants Commission, INDIA for the financial support provided in the form of a Research Fellowship to carry out this research work at IIT Hyderabad. The second author’s research was supported by the SERB grant MTR/2018/000137.

References

Armana, C., ‘Coefficients of Drinfeld modular forms and Hecke operators’, J. Number Theory 131(8) (2011), 1435–1460.CrossRefGoogle Scholar
Bandini, A. and Valentino, M., ‘On the Atkin ${U}_t$ -operator for ${\varGamma}_1(t)$ -invariant Drinfeld cusp forms’, Int. J. Number Theory 14(10) (2018), 2599–2616.CrossRefGoogle Scholar
Bandini, A. and Valentino, M., ‘On the Atkin ${U}_t$ -operator for ${\varGamma}_0(t)$ -invariant Drinfeld cusp forms’, Proc. Amer. Math. Soc. 147(10) (2019), 4171–4187.CrossRefGoogle Scholar
Bandini, A. and Valentino, M., ‘On the structure and slopes of Drinfeld cusp forms’, Exp. Math. 31(2) (2022), 637–651.CrossRefGoogle Scholar
Bandini, A. and Valentino, M., ‘Drinfeld cusp forms: oldforms and newforms’, J. Number Theory 237(8) (2022), 124–144.CrossRefGoogle Scholar
Bandini, A. and Valentino, M., ‘Hecke operators and Drinfeld cusp forms of level $t$ ’, Bull. Aust. Math. Soc., to appear. Published online (15 June 2022).CrossRefGoogle Scholar
Cornelissen, G., ‘A survey of Drinfeld modular forms’, in: Drinfeld Modules, Modular Schemes and Applications (eds. Gekeler, E.-U., van der Put, M., Reversat, M. and Van Geel, J.) (World Scientific Publishing, River Edge, NJ, 1997), 167–187.Google Scholar
Dalal, T. and Kumar, N., ‘The structure of Drinfeld modular forms of level ${\varGamma}_0(T)$ and applications’, Preprint, 2021, arxiv:2112.04210.Google Scholar
Dalal, T. and Kumar, N., ‘ On mod $p$ congruences for Drinfeld modular forms of level $pm$ ’, J. Number Theory 228 (2021), 253–275.CrossRefGoogle Scholar
Gekeler, E.-U., ‘On the coefficients of Drinfeld modular forms’, Invent. Math. 93(3) (1988), 667–700.CrossRefGoogle Scholar
Gekeler, E.-U. and Reversat, M., ‘Jacobians of Drinfeld modular curves’, J. reine angew. Math. 476 (1996), 27–93.Google Scholar
Goss, D., ‘ $\pi$ -adic Eisenstein series for function fields’, Compos. Math. 41(1) (1980), 3–38.Google Scholar
Goss, D., ‘ Modular forms for ${F}_r\left[T\right]$ ’, J. reine angew. Math. 317 (1980), 16–39.Google Scholar
Joshi, K. and Petrov, A., ‘On the action of Hecke operators on Drinfeld modular forms’, J. Number Theory 137 (2014), 186–200.CrossRefGoogle Scholar
Li, W. C., ‘Newforms and functional equations’, Math. Ann. 212 (1975), 285–315.CrossRefGoogle Scholar
Petrov, A., ‘ $A$ -expansions of Drinfeld modular forms’, J. Number Theory 133(7) (2013), 2247–2266.CrossRefGoogle Scholar
Schweizer, A., ‘Hyperelliptic Drinfeld modular curves’, in: Drinfeld Modules, Modular Schemes and Applications (eds. Gekeler, E.-U., van der Put, M., Reversat, M. and Van Geel, J.) (World Scientific Publishing, River Edge, NJ, 1997), 330–343.Google Scholar
Serre, J.-P., ‘Formes modulaires et fonctions zêta $p$ -adiques’, in: Modular Functions of One Variable, III, Lecture Notes in Mathematics, 350 (eds. Kuijk, W. and Serre, J.-P.) (Springer, Berlin, 1973), 191–268.CrossRefGoogle Scholar
Valentino, M., ‘Atkin–Lehner theory for Drinfeld modular forms and applications’, Ramanujan J. 58 (2022), 633–649.CrossRefGoogle Scholar
Vincent, C., ‘ On the trace and norm maps from ${\varGamma}_0(p)$ to $\mathrm{GL}_2(A)$ ’, J. Number Theory 142 (2014), 18–43.CrossRefGoogle Scholar

Save article to Kindle

To save this article to your Kindle, first ensure coreplatform@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

NOTES ON ATKIN–LEHNER THEORY FOR DRINFELD MODULAR FORMS
Available formats
×

Save article to Dropbox

To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.

NOTES ON ATKIN–LEHNER THEORY FOR DRINFELD MODULAR FORMS
Available formats
×

Save article to Google Drive

To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.

NOTES ON ATKIN–LEHNER THEORY FOR DRINFELD MODULAR FORMS
Available formats
×
×

Reply to: Submit a response

Please enter your response.

Your details

Please enter a valid email address.

Conflicting interests

Do you have any conflicting interests? *