Hostname: page-component-8448b6f56d-mp689 Total loading time: 0 Render date: 2024-04-19T05:04:55.893Z Has data issue: false hasContentIssue false
  • English
  • Français

DISTINCT SOLUTIONS TO GENERATED JACOBIAN EQUATIONS CANNOT INTERSECT

Part of: Elliptic equations and systems

Published online by Cambridge University Press:  20 February 2020

CALE RANKIN Open the ORCID record for CALE RANKIN [Opens in a new window]
CALE RANKIN*
Affiliation:
Mathematical Sciences Institute, Australian National University, Canberra, ACT 2601, Australia email cale.rankin@anu.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that if two 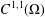$C^{1,1}(\unicode[STIX]{x1D6FA})$ solutions of the second boundary value problem for the generated Jacobian equation intersect in $\unicode[STIX]{x1D6FA}$ then they are the same solution. In addition, we extend this result to 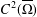$C^{2}(\overline{\unicode[STIX]{x1D6FA}})$ solutions intersecting on the boundary, via an additional convexity condition on the target domain.

Keywords

Jacobian equationsMonge–Ampère equationsuniqueness

MSC classification

Primary: 35J60: Nonlinear elliptic equations
Secondary: 35J96: Elliptic Monge-Ampère equations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 3 , December 2020 , pp. 462 - 470
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research is supported by an Australian Government Research Training Program (RTP) Scholarship.

References

Alexandroff, A., ‘Existence and uniqueness of a convex surface with a given integral curvature’, C. R. (Doklady) Acad. Sci. URSS (N.S.) 35 (1942), 131–134.Google Scholar
Evans, L. C. and Gariepy, R. F., Measure Theory and Fine Properties of Functions, revised edition, Textbooks in Mathematics (CRC Press, Boca Raton, FL, 2015).10.1201/b18333CrossRefGoogle Scholar
Figalli, A., The Monge–Ampere Equation and its Applications, Zurich Lectures in Advanced Mathematics, Book 22 (European Mathematical Society, Zurich, 2017).10.4171/170CrossRefGoogle Scholar
Gilbarg, D. and Trudinger, N. S., Elliptic Partial Differential Equations of Second Order, Classics in Mathematics (Springer, Berlin, 2001), reprint of 1998 edition.10.1007/978-3-642-61798-0CrossRefGoogle Scholar
Guillen, N. and Kitagawa, J., ‘Pointwise estimates and regularity in geometric optics and other generated Jacobian equations’, Comm. Pure Appl. Math. 70(6) (2017), 1146–1220.10.1002/cpa.21691CrossRefGoogle Scholar
Jhaveri, Y., ‘Partial regularity of solutions to the second boundary value problem for generated Jacobian equations’, Methods Appl. Anal. 24(4) (2017), 445–475.Google Scholar
Jiang, F. and Trudinger, N. S., ‘On the second boundary value problem for Monge–Ampère type equations and geometric optics’, Arch. Ration. Mech. Anal. 229(2) (2018), 547–567.10.1007/s00205-018-1222-8CrossRefGoogle Scholar
Liu, J. and Trudinger, N. S., ‘On the classical solvability of near field reflector problems’, Discrete Contin. Dyn. Syst. 36(2) (2016), 895–916.Google Scholar
McCann, R. J., ‘Existence and uniqueness of monotone measure-preserving maps’, Duke Math. J. 80(2) (1995), 309–323.10.1215/S0012-7094-95-08013-2CrossRefGoogle Scholar
Trudinger, N. S., ‘On the local theory of prescribed Jacobian equations’, Discrete Contin. Dyn. Syst. 34(4) (2014), 1663–1681.10.3934/dcds.2014.34.1663CrossRefGoogle Scholar