Article contents
CLASSIFICATION OF TETRAVALENT 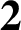 $\textbf{2}$-TRANSITIVE NONNORMAL CAYLEY GRAPHS OF FINITE SIMPLE GROUPS
$\textbf{2}$-TRANSITIVE NONNORMAL CAYLEY GRAPHS OF FINITE SIMPLE GROUPS
Published online by Cambridge University Press: 11 January 2021
Abstract
A graph
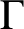 $\Gamma $
is called
$\Gamma $
is called
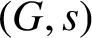 $(G, s)$
-arc-transitive if
$(G, s)$
-arc-transitive if
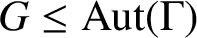 $G \le \text{Aut} (\Gamma )$
is transitive on the set of vertices of
$G \le \text{Aut} (\Gamma )$
is transitive on the set of vertices of
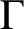 $\Gamma $
and the set of s-arcs of
$\Gamma $
and the set of s-arcs of
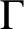 $\Gamma $
, where for an integer
$\Gamma $
, where for an integer
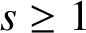 $s \ge 1$
an s-arc of
$s \ge 1$
an s-arc of
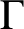 $\Gamma $
is a sequence of
$\Gamma $
is a sequence of
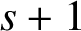 $s+1$
vertices
$s+1$
vertices
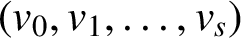 $(v_0,v_1,\ldots ,v_s)$
of
$(v_0,v_1,\ldots ,v_s)$
of
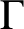 $\Gamma $
such that
$\Gamma $
such that
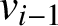 $v_{i-1}$
and
$v_{i-1}$
and
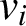 $v_i$
are adjacent for
$v_i$
are adjacent for
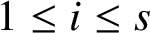 $1 \le i \le s$
and
$1 \le i \le s$
and
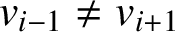 $v_{i-1}\ne v_{i+1}$
for
$v_{i-1}\ne v_{i+1}$
for
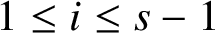 $1 \le i \le s-1$
. A graph
$1 \le i \le s-1$
. A graph
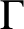 $\Gamma $
is called 2-transitive if it is
$\Gamma $
is called 2-transitive if it is
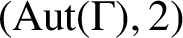 $(\text{Aut} (\Gamma ), 2)$
-arc-transitive but not
$(\text{Aut} (\Gamma ), 2)$
-arc-transitive but not
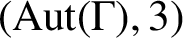 $(\text{Aut} (\Gamma ), 3)$
-arc-transitive. A Cayley graph
$(\text{Aut} (\Gamma ), 3)$
-arc-transitive. A Cayley graph
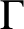 $\Gamma $
of a group G is called normal if G is normal in
$\Gamma $
of a group G is called normal if G is normal in
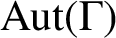 $\text{Aut} (\Gamma )$
and nonnormal otherwise. Fang et al. [‘On edge transitive Cayley graphs of valency four’, European J. Combin.25 (2004), 1103–1116] proved that if
$\text{Aut} (\Gamma )$
and nonnormal otherwise. Fang et al. [‘On edge transitive Cayley graphs of valency four’, European J. Combin.25 (2004), 1103–1116] proved that if
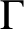 $\Gamma $
is a tetravalent 2-transitive Cayley graph of a finite simple group G, then either
$\Gamma $
is a tetravalent 2-transitive Cayley graph of a finite simple group G, then either
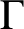 $\Gamma $
is normal or G is one of the groups
$\Gamma $
is normal or G is one of the groups
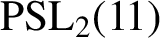 $\text{PSL}_2(11)$
,
$\text{PSL}_2(11)$
,
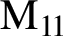 ${\rm M} _{11}$
,
${\rm M} _{11}$
,
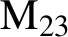 $\text{M} _{23}$
and
$\text{M} _{23}$
and
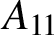 $A_{11}$
. However, it was unknown whether
$A_{11}$
. However, it was unknown whether
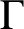 $\Gamma $
is normal when G is one of these four groups. We answer this question by proving that among these four groups only
$\Gamma $
is normal when G is one of these four groups. We answer this question by proving that among these four groups only
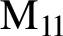 $\text{M} _{11}$
produces connected tetravalent 2-transitive nonnormal Cayley graphs. We prove further that there are exactly two such graphs which are nonisomorphic and both are determined in the paper. As a consequence, the automorphism group of any connected tetravalent 2-transitive Cayley graph of any finite simple group is determined.
$\text{M} _{11}$
produces connected tetravalent 2-transitive nonnormal Cayley graphs. We prove further that there are exactly two such graphs which are nonisomorphic and both are determined in the paper. As a consequence, the automorphism group of any connected tetravalent 2-transitive Cayley graph of any finite simple group is determined.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 104 , Issue 2 , October 2021 , pp. 263 - 271
- Copyright
- © 2020 Australian Mathematical Publishing Association Inc.
Footnotes
X. G. Fang and J. Wang were supported by the National Natural Science Foundation of China (Grant No. 11931005). S. Zhou was supported by the Research Grant Support Scheme of The University of Melbourne.
References
- 1
- Cited by



