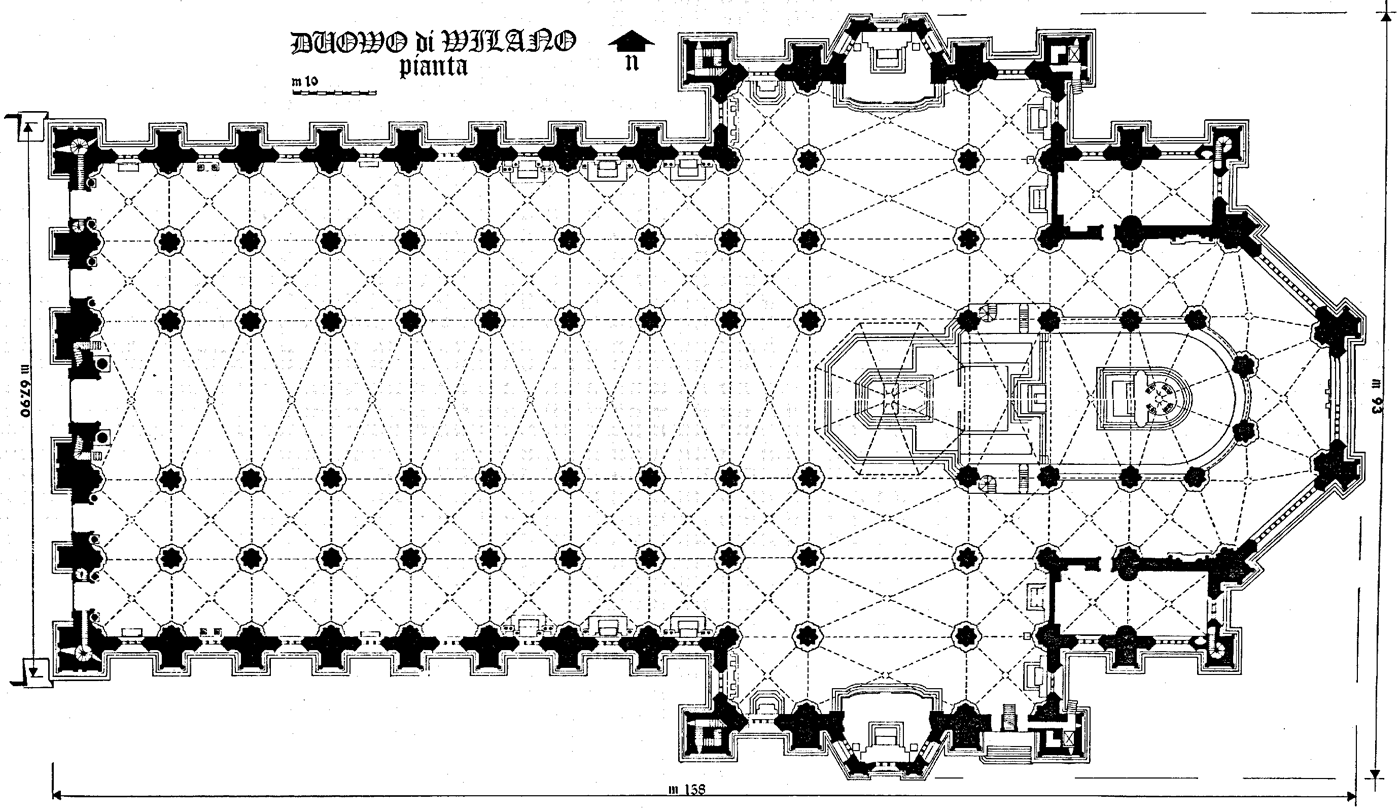
The construction of Milan Cathedral, from 1386, was one of the most important episodes in the history of Italian and European architecture (Fig. 1). This was, first, because of the uniqueness of the building itself, the largest Gothic church ever constructed in Italy; secondly, because of the input of some of the most authoritative architects of the late fourteenth and fifteenth centuries in Europe (Lombard, French, German), who were invited from time to time to make architectural and structural proposals; and, thirdly, because the project initiated debates and discussions continuing for over a century, regarding structural choices and differing Lombard and Northern European building practices, as well as about the affirmation of ducal or communal authority.Footnote 1 Indeed, the documentation of the late Trecento and early Quattrocento discussions about how to build the cathedral, made famous to English readers in a celebrated article by James Ackerman, is extraordinarily rich and extensive, and permits a consideration of the project from many points of view including, in particular, the relationship between medieval architectural theory and an actual project. At the same time, however, the subject is very complex, and any enquiry has to contend with the copious modern literature and the conclusions that have been reached hitherto – often erroneously in our view – about many of the most salient points.Footnote 2

Fig. 1. Façade of Milan Cathedral
The most important matter discussed in the great early debates concerned the format of the building's elevation. The ground-plan laid out in 1386 was based on a system of squares for the four side-aisles, with interaxial dimensions of 16-by-16 braccia, and rectangles for the nave of 16-by-32 braccia.Footnote 3 As the walls of the East end rose, a decision over the heights of the principal elevational elements – the piers and the nave- and aisle-vaults – became urgent. It is often claimed that the heated disputes concerned the question of whether the two aisles on either side should be of the same or of different height; and whether the elevation, partly conditioned by the 16-by16-braccia grid used for the ground-plan, should rise in a rectangular or triangular – or in an ad quadratum or ad triangulum – configuration. The definitive solution, presented to the authorities by Gabriele Stornaloco in late 1391 in the form of a letter and drawing, was one that involved equilateral triangles overlaid onto rectangles which generated only slightly different heights for the piers, imposts and vaults of the aisles and nave, but which Stornaloco and the master-builders treated as equal. This solution, as we shall see, was the only one with which ‘pointed-third’ vaults, the type with arcs defined by equilateral triangles that was used throughout the cathedral, could be generated (see Fig. 6).
The rich nineteenth- and twentieth-century literature on the early disputes, however, complicates matters considerably, and has, as we will argue, confused a number of the saga's cardinal points. Stornaloco's text and diagram, known only from copies of copies, have never been published in coherent Latin and we attempt to rectify that here (Appendix I), but this is just one of several problems that have contributed to present-day misconceptions. These include, first, that the Milanese master-masons were incapable of determining the heights of triangles for themselves and that Stornaloco was summoned to do so for them, and that he employed an impenetrably complicated formula; secondly, that Stornaloco's scheme of 1391 was then abandoned in 1392 for another based on isosceles, rather than equilateral, triangles; and, finally, that the Milanese had also been considering an elevational format based on rectangles of 16-by-10 braccia, which, it is usually claimed, is illustrated in a well-known drawing attributed to Antonio di Vincenzo (see Fig. 10).
In contrast to such views, we will propose a very different interpretation of the documents. We will argue, first, that the master-masons were perfectly capable of determining the heights of triangles without the need of a geometrician-mathematician, because they operated in a building-culture where practical geometry ruled over theoretical mathematics; and we will further argue that Stornaloco's role was to guarantee geometrically the validity of a system involving not only equilateral triangles but also rectangles and a circle, a hexagon and a square, and that the formula he used for calculating the heights of triangles was simple and not arcane in the slightest. We will also contend that the fact that the heights of the aisle- and nave-vaults as built are lower than in Stornaloco's original proposal – hereafter Stornaloco I – does not mean that his proposal was abandoned for one based on isosceles triangles, but that it was revised so that the imposts of the arches were lower than Stornaloco had originally suggested, a revision we will refer to henceforth as Stornaloco II. We will suggest, finally, that the elevational drawing attributed to Antonio di Vincenzo does not in fact record a project based on rectangles and that it is merely a bad copy of Stornaloco II, and so has limited value for the history of the debates over the design of the cathedral.
In addition to all this, we will be emphasising, again in contrast with prevailing opinion, that the Milanese master-masons were anything but amateurish, disorganised and incompetent by comparison with their foreign counterparts. We will be re-exploring in particular the much-vaunted discussions of 1400, in part a re-run of those of 1392, in which the French expert Jean Mignot proposed to return to the original Stornaloco I project, which, it emerges, had been devised at the outset by a German architect; and we will be concluding that Mignot's famous criticism of the Milanese, involving the respective merits of ars and scientia, had a very different meaning from the one generally accepted in the literature. This, we hope, will be of some interest not only to those concerned with architectural theory and architectural proportions but to medievalists in general.
1. STORNALOCO I AND ITS INTERPRETATIONS
The supremely important matter of devising a system for establishing the heights of the imposts and vaults of the nave and aisles was extensively and bitterly discussed in the late fourteenth and early fifteenth centuries. The definitive solution was presented, between 24 September and 13 October 1391, by Gabriele Stornaloco of Piacenza, an experto in arte geometrie, who, as we shall see, formalised a pre-existing project in an elegant document and drawing.Footnote 4
Stornaloco himself tells us that his scheme (Stornaloco I) is generated from the pre-established grid of the ground-plan of the cathedral,Footnote 5 with its squares of 16-by-16 braccia based on the interaxial distances between the piers (‘I have taken all the widths by measuring from axis to axis, so I have not bothered to set down the thickness of the piers in the drawing’; see Appendix I). The plan had fixed the total breadth of the cathedral at 96 braccia, comprising a nave of 32 braccia plus four aisles of 16 braccia each (Fig. 2).Footnote 6 Stornaloco developed the elevation by using equilateral triangles for the various heights, and employing multiples of 14 braccia (the approximate height of a triangle 16 braccia wide, which also corresponds to rectangles 16 braccia wide and 14 high).Footnote 7 Thus, the imposts of the outer aisle vaults were fixed at 28 braccia, those of the inner aisles at 42 braccia and those of the nave at 56 braccia, with the apex of the nave-vault set at 84 braccia (Fig. 3).
Fig. 2. Survey plan of Milan Cathedral (after Ferrari da Passano, ‘Storia della veneranda fabbrica’, 1973)
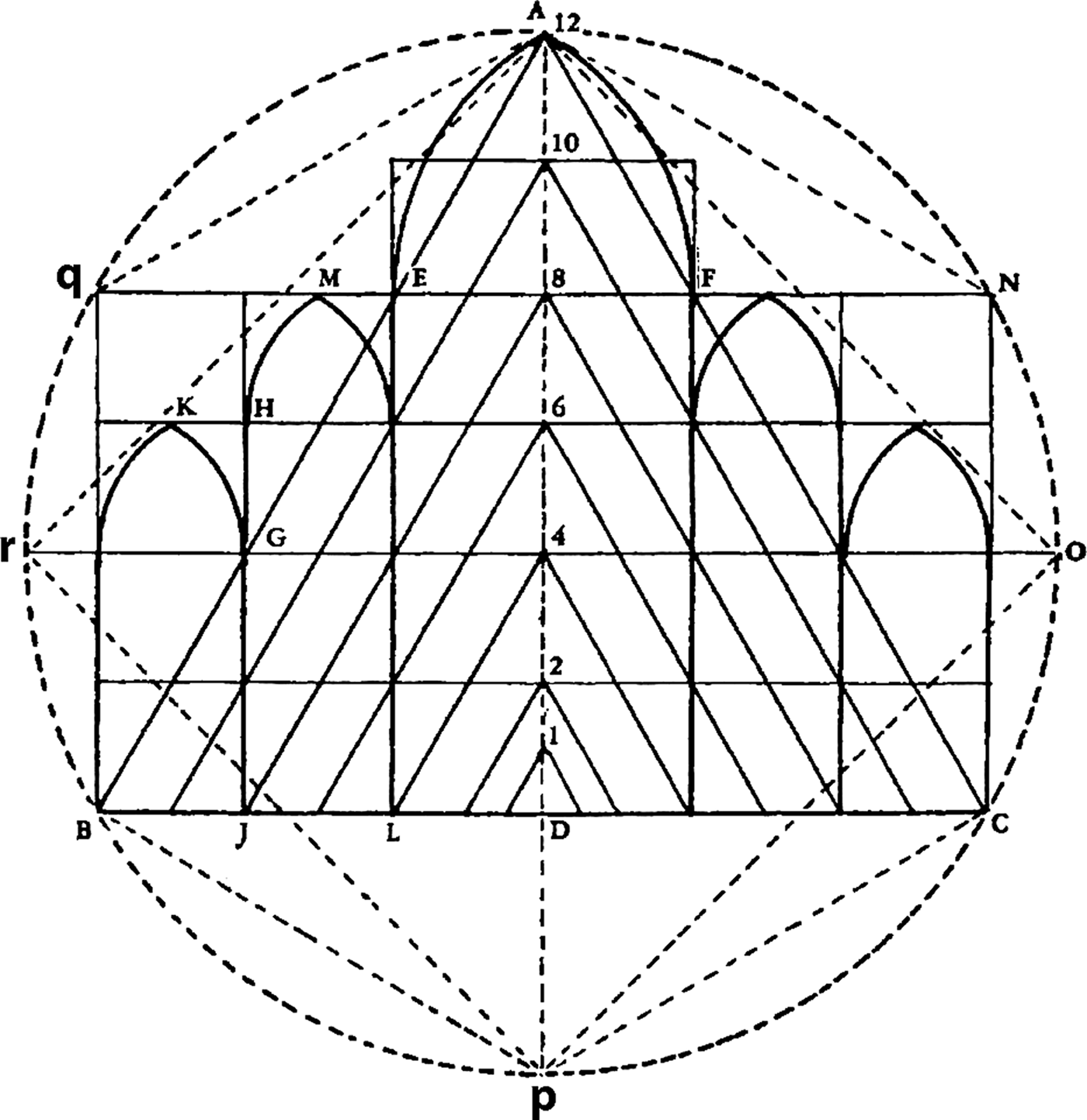
Fig. 3. Reconstruction of Stornaloco's scheme (after Frankl, ‘The Secret of the Mediaeval Masons’, 1945). Key (upper-letters are Frankl's; lower-case letters are ours): ABC = equilateral triangle; ANCpBq = hexagon; AOpr = square; BC = breadth of the nave and four aisles (96 braccia); EF = interaxial distance between the nave piers (32 braccia); D2 = unit of 14 braccia; D4 = imposts of the external aisle vaults (2 × 14 = 28 braccia); D6 = imposts of the internal aisle vaults (3 × 14 = 42 braccia); D8 = imposts of the nave vaults (4 × 14 = 56 braccia); D12 = height of the vertical axis of the triangle ABC = apex of the nave vault (6 × 14 = 84 braccia)
One is struck by the economy, elegance and simplicity of Stornaloco's method of conveying, in geometrical terms, the essential information about the principal dimensions and proportions of the elevation to the overseeing Fabbricieri. Once Stornaloco has described the fundamental geometric figures implicit in the elevation – the circle circumscribing the hexagon, as well as the equilateral triangle and the square – he mentions only three dimensions specifically: the first, 96 braccia, is the breadth of the nave and four aisles established before his intervention; the second, 84 braccia, is the height of the triangle indicating the apex of the nave-vault; and the third, 32 braccia, is the interaxial distance between the nave-piers. The other information he needed to provide concerned the heights of the imposts of the nave and inner aisles, and the heights of the vaults of both aisles; but he did not do this numerically but geometrically by identifying these points in relation to the apexes of a series of equilateral triangles. It is not entirely clear why he needed the twelve triangles, which he indicated with numbers on the axis AD in his diagram, since he could have established all the essential heights with just four: that is, triangle 4 (iiij) for the height of the imposts of the outer aisles; triangle 6 (vj) for the outer-aisle vaults and inner-aisle imposts; triangle 8 (viij) for the inner-aisle vaults and the nave imposts; triangle 12 (xij) for the nave vault (see Figs 15 and 16).
It is here that we encounter the fascinating problem that gripped the attention of scholars from Paul Frankl onwards: how did Stornaloco carry out his calculations and why was his intervention necessary? Frankl, like Camillo Boito and Luca Beltrami before him, insisted on what had been known since the ancient world: that the height of an equilateral triangle is incommensurable with respect to its base or side, but equals the base multiplied by √3/2, to use modern mathematical notation. Frankl therefore asked how the master-masons could have used a system of equilateral triangles if they were only able to draw them geometrically but were not capable of calculating their heights.Footnote 8 Having posed the problem in this form, he then proposed that Stornaloco had been summoned to Milan to calculate these dimensions.Footnote 9
Although Stornaloco's original text has been lost and is available to us only in various copies, the transcriptions are for the most part easy to understand so that almost anybody can redraw the elevation Stornaloco proposed following his text step-by-step, as has been done by a number of scholars, including Frankl (Fig. 3).Footnote 10 The only obscure point, in fact, is the way in which Stornaloco arrived at his declaration that the height of an equilateral triangle with a base of 96 units was ‘slightly less’ than 84 units (in fact 83.138 units in present-day decimal notation). If this had been the main reason for Stornaloco being called to Milan, and if, indeed, it had been regarded as the most difficult problem to be resolved, it seems extraordinary that this very point is not explained in his text and is passed over so rapidly as to seem incomprehensible, since this would have made his visit entirely useless for the master-masons.
The key passage is this:
The base of the triangle is the line BC and this is the width of the church, i.e. 96 quantitates. Therefore the line AD, which is the height of the summit of the church, will be the square root resulting from ‘dix dc dcc mxx sesara quie tregesime’, which is something less than 84 (Beltrami's version, left without corrections; for a more accurate transcription see Appendix I).
As is well known, it was Erwin Panofsky who proposed, at Frankl's request, an interpretation of the passage, and this has generally been accepted, even though Panofsky made it clear that it included much that is uncertain.Footnote 11 To avoid the relatively complicated process of extracting a square root and arriving instead at an approximation, he proposed that a ‘formula’ must have been used: but he unjustifiably omitted part of Beltrami's text and after a long discussion concluded that the extract cited above implied a mathematical expression according to which ten times half the required height equals roughly the length of the base or side of the triangle multiplied by 100 and then by 700, the result being divided by 1010.Footnote 12 Such a ‘formula’, we can declare without hesitation, seems excessively complicated, and is anything but a simplification of the problem.
More recently Peter Kidson – who, unfortunately, ignored all the literature on the cathedral apart from Frankl and Panofsky – proposed a different explanation of Stornaloco's supposed formula.Footnote 13 According to Kidson, the master-masons were capable of calculating the approximate height of an equilateral triangle, but required greater precision from Stornaloco.Footnote 14 So, via a tortuous origami-like procedure involving nine right-angled triangles, Stornaloco, Kidson argues, would have applied Archimedes's formula for the extraction of the square-root of three (corresponding to the fraction 265/153) by geometry rather than arithmetic. The fact that Stornaloco, according to Kidson, did not explain this most difficult step was deliberate.Footnote 15 The aim was to keep the formula secret by using terminology that was ‘deceptive as well as esoteric’Footnote 16 and therefore incomprehensible to anyone outside a circle of educated initiates. The value of Stornaloco's visit, Kidson suggests, resulted from the consultation itself, which gave legitimacy to the project through its approval by an expert mathematician.Footnote 17 But Kidson's explanation suffers from the same difficulty as Panofsky's – it is one of excessive and unnecessary complexity.
If one were to believe Panofsky's or Kidson's interpretation, the mathematics adopted by Stornaloco was shrouded in esoteric mystery and ingenious complication so as to keep its ‘secret’ inaccessible. But these proposals have nothing to do with what contemporary manuals teach us, as was highlighted by the historian of science Guy Beaujouan as long ago as 1963, who offered a far simpler solution.Footnote 18 His proposal was that mediaeval mathematicians used an easily memorised fraction, one of 26/30, to work out the height of an equilateral triangle relative to its base with an acceptable degree of accuracy. So it is reasonable to suppose that Stornaloco may have used the same expression to calculate his figure of slightly less than 84 braccia, this being equal to 96 braccia multiplied by such a fraction. In this light, Beaujouan then suggested amending the text cited above to read as follows:
Therefore the line AD which will be the height of the summit of the church is the square-root resulting from multiplying [96] by 26, which are thirtieths, which is something less than 84.Footnote 19
One can quibble with the details of Beaujouan's proposal but the principle behind his explanation of Stornaloco's calculation seems far more attractive than others proposed so far.
2. PRACTICAL GEOMETRY VERSUS MATHEMATICS IN THE DESIGN-PROCESS
So let us now reconsider the assumption expressed by Frankl and many others that Stornaloco was summoned to Milan because the master-masons could not calculate the height of equilateral triangles with numbers.
In his famous article of 1945, Frankl starts his investigation from the conviction that the medieval masons did not use yardsticks (or foot rules) – a key point made several times in his text – or scale drawings, and was looking for ‘a method necessary to translate sketches into working size’.Footnote 20 He found the solution in Bernhard Kossmann's theory of the ‘Great Unit’,Footnote 21 a module of whole numbers (for instance 5, 6 or 7 feet) employed, according to him, for both projecting and construction. Analysing the documents about Milan Cathedral, therefore, he proposed that for the plan they used an 8-braccia ‘Great Unit’, which took the form of a wooden lath 4.6 m long, and then, for the first project for the elevation (which, according to him, was represented in Antonio di Vincenzo's drawing; see Section 7), a 10-braccia ‘Great Unit’, for which they would have used a lath of 5 braccia (3 m) long.Footnote 22 And, according to Frankl, when the authorities decided instead to adopt Stornaloco's project based on equilateral triangles, the master-masons were unable to calculate the heights of the triangles numerically, so they were obliged to summon the mathematician for assistance.Footnote 23 Frankl, therefore, seems to imagine that the master-masons were practically innumerate, and equipped with only a scanty knowledge of only the most elementary rules of geometry, and were therefore incapable of carrying out any numerical operations.Footnote 24 He proposed that in Stornaloco's original scheme of 1391 the mathematician had used a ‘Great Unit’ of 7 braccia to communicate his project to master-masons, while at the meeting of 1392 the Deputati chose to change this ‘Great Unit’ to one of 6 braccia, to cater for the proportions of the Pythagorean triangles, a decision which, according to most scholars, was then adopted (see Section 4).Footnote 25 In Frankl's view, therefore, the ‘Great Unit’ was a sort of universal practical device for translating geometrical proportions into an actual building.
What was not taken into account, however, was that before the establishment and diffusion of Hindu-Arabic numbers and the arithmetic associated with them, geometry had been preferred in architectural practice to numbers for centuries precisely because of its universality and simplicity. Geometry was valid everywhere, with any unit of measurement and at any scale; and geometric design procedures were easy to remember with simple step-by-step techniques and could readily be handled on the building site, and by using them the master-masons could derive dimensions corresponding to irrational numbers without having to resort to arithmetic. In fact, by using geometrical schemes drawn to scale on pieces of paper or on flat-surfaces, the master-masons were perfectly capable of measuring incommensurable dimensions such as the height of an equilateral triangle, and of rounding them up or down to the nearest whole number, thereby ‘translating’ these geometric proportions into approximate arithmetical equivalents to be used in a building.
Franklin Toker arrived at the same conclusion through an analysis of a drawing for the façade of Palazzo Sansedoni in Siena of 1340. The drawing is a freehand copy, made for legal purposes, of a more accurate drawing that would have been prepared for the builders, and it is accompanied by a written contract specifying further instructions that could not be represented on the drawing. In this connection, Toker concluded that the project relied on scale-drawings, so that, working very economically, ‘the architect would draw a geometric construction such as the ad triangulum on scaled paper and read off its whole-number equivalents’.Footnote 26 In fact, a similar use of simple, easily remembered geometrical formulas is described by Cesare Cesariano when commenting on the atrium in his edition of Vitruvius (1521). There he illustrates a simple geometrical construction for establishing the value of √2 (the relationship between the side and diagonal of a square), which yields a very good approximation of 12:17½.Footnote 27
Frankl's assertion that a
knowledge of the most elementary rules of geometry was not universally widespread in medieval times. Only those who had been educated in the seven artes liberales, including the ars geometriae, possessed any mathematical culture ….Footnote 28
is unacceptable because a theoretical mathematical training and a knowledge of practical geometry are two very different things.Footnote 29 If building-sites were populated by masters without calibrated yardsticks and with no knowledge of elementary practical geometry, then the construction of buildings would have been impossible, and all the more so in the case of a structure as complicated as a cathedral. The need to coordinate the operations of the master-masons made a common language essential and this, we suggest, was the role of practical geometry. Its importance is demonstrated by the fact that amongst the first books to be printed were the late fifteenth- and early sixteenth-century design handbooks by Mathes Roriczer, Hans Shmuttermayer and Lorenz Lechler, which provide practical instructions, accompanied by drawings, illustrating some of the steps needed for a correct design of some architectural elements, steps which at first sight might seem to require mathematical calculation (Fig. 4).Footnote 30 In fact, however, their instructions come in the form of easy practical rules, based on simple geometric figures, which can be employed following a prefixed set of steps, without any need for analytical reasoning or formulae.Footnote 31
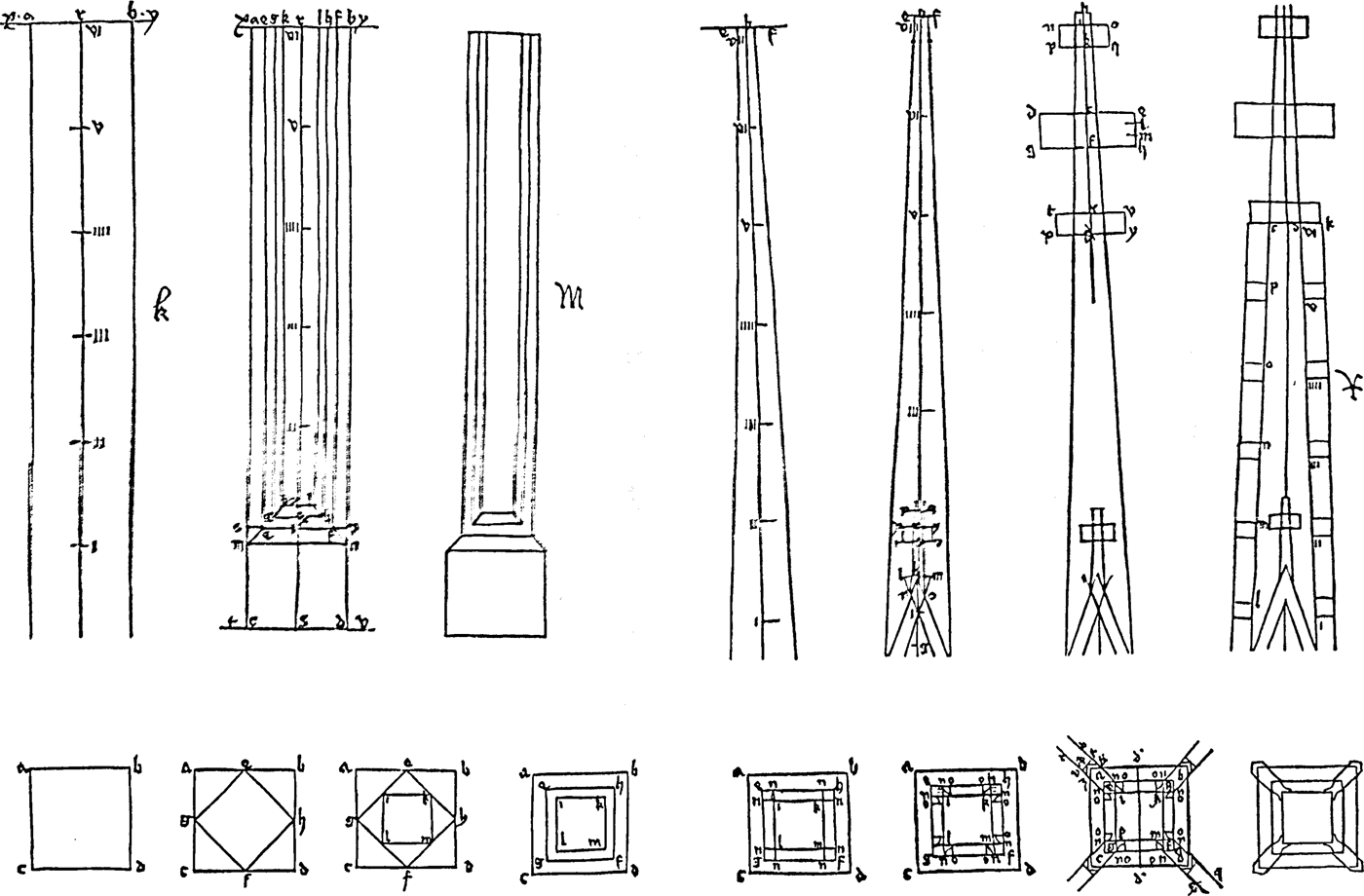
Fig. 4. Mathes Roriczer, illustrations showing how to design a pinnacle by ‘constructive geometry’, starting from a square (from Büchlein von der Fialen Gerechtigkeit, 1486)
Lon R. Shelby, evidently in reaction to Frankl, has looked more deeply into what kind of geometrical knowledge was possessed by master-builders at the time.Footnote 32 Their familiarity with ‘practical geometry’,Footnote 33 he argues, did not derive from a formal scholastic education, since geometry in the academic sense was only studied at advanced levels, but instead, from an oral training acquired on building-sites and in workshops, to which the thirteenth-century ‘notebook’ of Villard de Honnecourt is an excellent witness. The procedures illustrated by Villard, like those in the three manuals mentioned above from the late fifteenth- and early sixteenth centuries, do not require arithmetical calculations or a knowledge of theorems, even though numbers were, of course, an integral part of constructional geometry; instead they are ‘very simple, very physical, and very non-mathematical’.Footnote 34
Finally, Stornaloco's report confirms the pre-eminence of geometry over numbers in the design-process, since he concludes it by stating that
it is sufficiently clear to the master-builders how much space they [the piers] occupy in the bodies of the church; furthermore, with respect to the width and the area, a great deal could be quantified numerically as to how all the bodies represented in the drawing are related according to the geometrical constructions, but I omit this on account of its length. [Our italics]
In other words, the dimensions in numbers can easily be derived from the geometrical figures using universally understood procedures.
It also seems curious that Frankl based part of his argument on the belief that stone-masons did not use scales or calibrated yardsticks, so that ‘the medieval architect had to choose measurements which his mason could execute without a yardstick’.Footnote 35 For it is an indisputable fact that in very many Italian cities – including Ascoli Piceno, Assisi, Bologna, Cesena, Padova, Parma, Piacenza, Rimini, San Marino, Todi, Treviso, Verona and Vicenza – there are stone reliefs with public units of measurement that still survive on town halls (Fig. 5). It is also the case that the architect or master-mason is almost always represented in paintings and written documents as carrying a measuring-rod (virga).Footnote 36 Moreover, Frankl's argument that it was impossible for master-masons to rely on numerical measurements, owing to the variability of units of measurement from city to city, and therefore had to rely, instead, on the indispensable ‘Great Unit’,Footnote 37 which is the hinge of his argument, seems extremely unlikely in a world in which the movement of master-builders from building-site to building-site and city to city was commonplace. Indeed, master-masons were certainly well-accustomed to using different units of measurement in the sixteenth century when we find Baldassare Peruzzi and Antonio da Sangallo the Younger indicating various different local units of measurement on their drawings, such as Sienese or Florentine braccia in Tuscany and palmi in Rome.Footnote 38 Frankl's account, therefore, seems to have been aimed above all at demonstrating the existence of the ‘Great Unit’ as a basis for the design and construction of buildings, despite the fact that in the extensive documentation on the cathedral in Milan there is no trace of any such thing.

Fig. 5. Assisi, Torre del Popolo, public units of measurement, 1349. Note the three metal rods, at the bottom and left, indicating lengths (canna, passetto, palmo)
As regards Frankl's and Panofsky's idea that medieval drawings were not made to scale, Toker has shown, instead, that a great many were made to a precise scale, which was frequently 1:48. In a duodecimal system, which was widespread even though the units of measurement varied, this meant that a quarter of the submultiple represented the given unit (so that, for example, a quarter of an inch represented one braccio), which was thus a simple and easy-to-use ratio. Other scales employed were 1:12 and 1:20, which were likewise suitable for units of measurement divisible by 12, such the Milanese braccio, or by 20, such as the Florentine or Sienese braccio.Footnote 39
There are many sources that confirm the widespread use of scaled drawings across Europe by the fourteenth century and even during the previous century, indicating that architects were directing building operations by ‘remote control’ by means of drawings. These drawings, of plans and elevations, would have been the equivalent of modern working drawings, although they were less detailed and required a certain familiarity with the current language and traditions of construction.Footnote 40
So the ‘problem’ at Milan Cathedral in the late Trecento regarding the establishment of the various internal heights was hardly to do with the incapacity of the master-builders to calculate these heights on the basis of equilateral triangles – for if it had been then nobody would have used this type of geometrical scheme, which was certainly nothing new in 1391. This being so, we still need to ask why it was that Stornaloco was invited to Milan.
3. STORNALOCO'S ROLE IN THE CONCEPTION AND DEVELOPMENT OF THE PROJECT
If the master-builders were perfectly capable of determining the heights of triangles, then why did the authorities need to summon Stornaloco, a mathematician and expert in geometry? Following Beaujouan, our reply is that they did not send for him merely to work out a simple formula that was widely used to determine the heights of triangles, and that the answer is already implicit, in part, in the conclusion of Frankl's essay as well as in Ackerman's article.Footnote 41 It concerns his understanding of geometry as the basis of the best architectural design. The square and the equilateral triangle are shapes that feature frequently in architectural writings from Vitruvius to Villard de Honnecourt, and they were regarded as sacred from the time of Plato, belonging to ‘a geometrical élite’ that gave rise to a powerful tradition which continued uninterrupted for centuries.Footnote 42 Given the desire to construct a cathedral, the House of God, identified with the highest good and with absolute beauty, it is obvious that the building had to be perfect, a Gesamtkunstwerk in which every element was harmoniously related to the whole as a reflection of the order of God's universe, as opposed to the disorder of the contemporary world, and one in which all forms and numbers could also be symbols.Footnote 43
Stornaloco's project thus coordinated the various parts of the cathedral coherently by working out the heights up to the nave vault, but it also suggested a more general and abstract harmony for the whole by showing how the structure of the sacred building was generated by a regular hexagon determining the total height of the inner aisles and the inclination of the future flying-buttresses above them, together with an equilateral triangle fixing the total height of the nave and a square, the diagonal of which established the height of the imposts of the outer-aisle vaults, all inscribed in the same circle.Footnote 44 As Sebastiano Serlio and Pietro Cataneo recall in their sixteenth-century treatises, a pair of compasses was also called a sesta (sixth) precisely because it allowed one to divide the circumference into six parts equal to its radius thus permitting the construction of an inscribed regular hexagon, a form assai perfetta (‘very perfect’) and, from this, an equilateral triangle.Footnote 45 And in fact Stornaloco's report begins with the construction of the circle circumscribing the hexagon, square and triangle. The height of the nave is then divided into six parts, involving rectangles (figurae quadrangulares, as Stornaloco himself described them) 16 units wide and 14 units high, and with a ratio of base-to-height roughly equal to that of the equilateral triangles marking the key-points of the elevation. Stornaloco, we can surmise, was the person able to formalise and validate such architectural design-decisions, some of which had certainly been taken before his arrival, with a scheme that was simultaneously geometrical, modular and theoretical, and which could guarantee at a stroke the constructional, formal, static and symbolic unity of the project (Fig. 6).Footnote 46
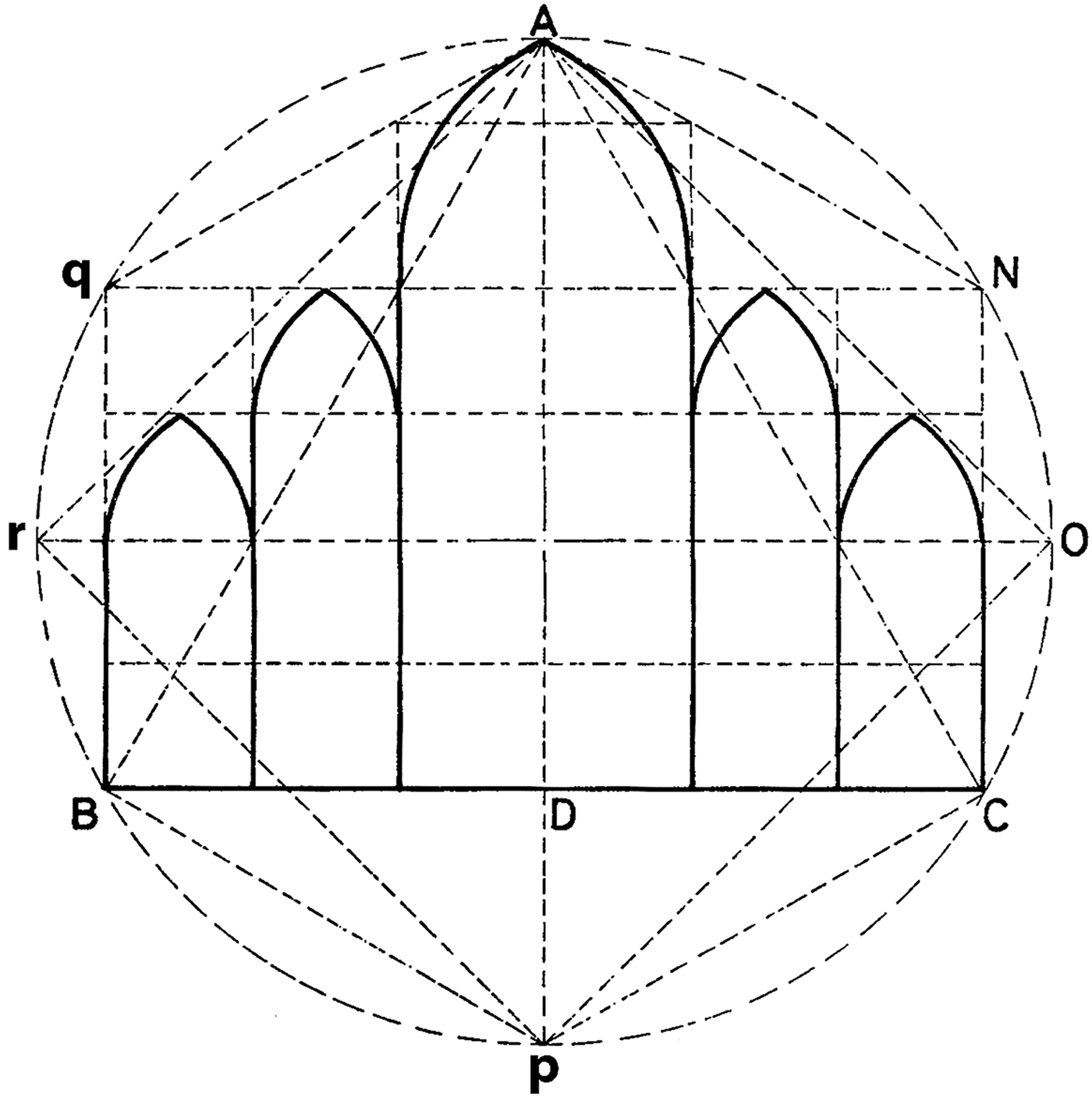
Fig. 6. Reconstruction of Stornaloco's scheme (after Valentini, Il duomo di Milano, 1990). Key (uppercase -letters are Valentini's; lower-case letters are ours): ANCpBq = regular hexagon inscribed in circle = height of the inner aisles and inclination of the future flying-buttresses; ABC = inscribed equilateral triangle generated by the hexagon = height of the nave; AOpr = inscribed square generated by the hexagon, with its diagonal rO establishing the height of the imposts of the outer aisle vaults; AD ÷ 6 = 14 = height of the ‘figure quadrangulares’ or ‘quadrati’; BC ÷ 6 = 16 = width of the ‘figure quadrangulares’ or ‘quadrati’; 16:14 = BC:AD
But we cannot determine just how much of the geometrical construct incorporated in Stornaloco's project had already been decided by others: that is, whether it was previous architects, the cathedral's Fabbriceri or Stornaloco himself who had elaborated on the basic ad triangulum scheme by adding the circle, hexagon and square, laden with cosmological significance. All we know for sure is that a system ad triangulum existed before Stornaloco's presence in 1391, as we shall see below.
Whilst there were discussions about various elevations ad triangulum or ad quadratum (i.e. schemes based on equilateral triangles or squares) there is no record of the existence of a model embodying any kind of elevational system before Stornaloco's contribution of 1391. The construction of a model always demonstrated the seriousness of a project given the time and money involved, and the likelihood is that, as we shall now see, the first wooden model of the cathedral was made so as to incorporate Stornaloco's scheme, thus indicating its absolute importance for the authorities.
Stornaloco, following his visit to Milan, returned to Piacenza by 13 October 1391 and then sent his letter to the Deputati. Very soon afterwards, on 29 October 1391, a carpenter from Stornaloco's home-town, called Simone, started working on a wooden model following the ‘design and advice’ of a certain Simone da Cavagnera.Footnote 47 On 18 April 1392, Cavagnera was instructed to transport the model from his home, where the carpenter was working, to the cathedral, and by 2 May it was about to be painted, and had therefore been completed.Footnote 48 Cavagnera was entrusted with overseeing the execution of the model and was not an appointed engineer of the cathedral. He was in fact one of the cathedral's Deputati mentioned a number of times in documents from 1387 until 1403, and he was certainly an expert in architecture.Footnote 49 The documents do not tell us exactly what the model represented, but, given that its construction started less than a month after Stornaloco's visit of September–October 1391, and that the carpenter was one of his countrymen and had presumably been recommended to the Deputati by Stornaloco himself, its function must have been to illustrate Stornaloco's initial project.Footnote 50 The model presumably represented part or even all of the cathedral in accordance with Stornaloco's scheme, but also showed the thicknesses of the piers and arches, which were lacking from his purely geometrical, skeleton-like diagram. The model was completed by the end of April 1392 and must have been consulted, along with Stornaloco's report and drawing, at the great meeting of 1 May 1392, when the authorities changed tack and adopted an adjusted version of Stornaloco's project – i.e. Stornaloco II – instantly making the model redundant.
The hypothesis that the model illustrated Stornaloco's first scheme – Stornaloco I – appears to be confirmed by the bizarre sequel to the May meeting. In September 1392, the Deputati decided to place the now useless model in a secluded spot in the cathedral, within an enclosure containing, at that time, the tombs of the archbishops Ottone and Giovanni I Visconti, ‘so that it could not be seen and should remain hidden, unless declared otherwise’.Footnote 51 It is perhaps not surprising, therefore, that in 1401 Simone da Cavagnera was determined to defend Mignot's attempt to return to Stornaloco I so strongly (Appendix II, doc. III).
The next task was to replace the Cavagnera model with another one incorporating the revisions adopted in Stornaloco II. This process was begun by 1394 when Giovannino de Grassis produced a sectional drawing, which does not survive, made at the level of the sacristies, that included the exterior and interior of the church and the various revised heights, and was not, therefore, related to the drawing attributed to Antonio di Vincenzo (see Section 7).Footnote 52 The next wooden model, which incorporated Stornaloco II, was made by Giovannino between 1395 and 1399 and it, eventually, even included the roofs.Footnote 53 This, presumably, was the model used as the basis for the celebrated discussions of 1400 with Mignot, and which remained on site until 1414 when we hear that the roofs of the model were still not finished.Footnote 54
4. THE TWO VERSIONS OF STORNALOCO'S PROJECT AND THEIR DIFFERING DIMENSIONS
There is another celebrated enigma concerning Stornaloco's project. The heights of the intradoses of the inner-aisle and nave vaults in the actual building are lower than those envisaged in Stornaloco I and seem to have been generated from units of 12 rather than 14 braccia. Was it, therefore, that Stornaloco's scheme was abandoned at the meeting in May 1392 and replaced by another?
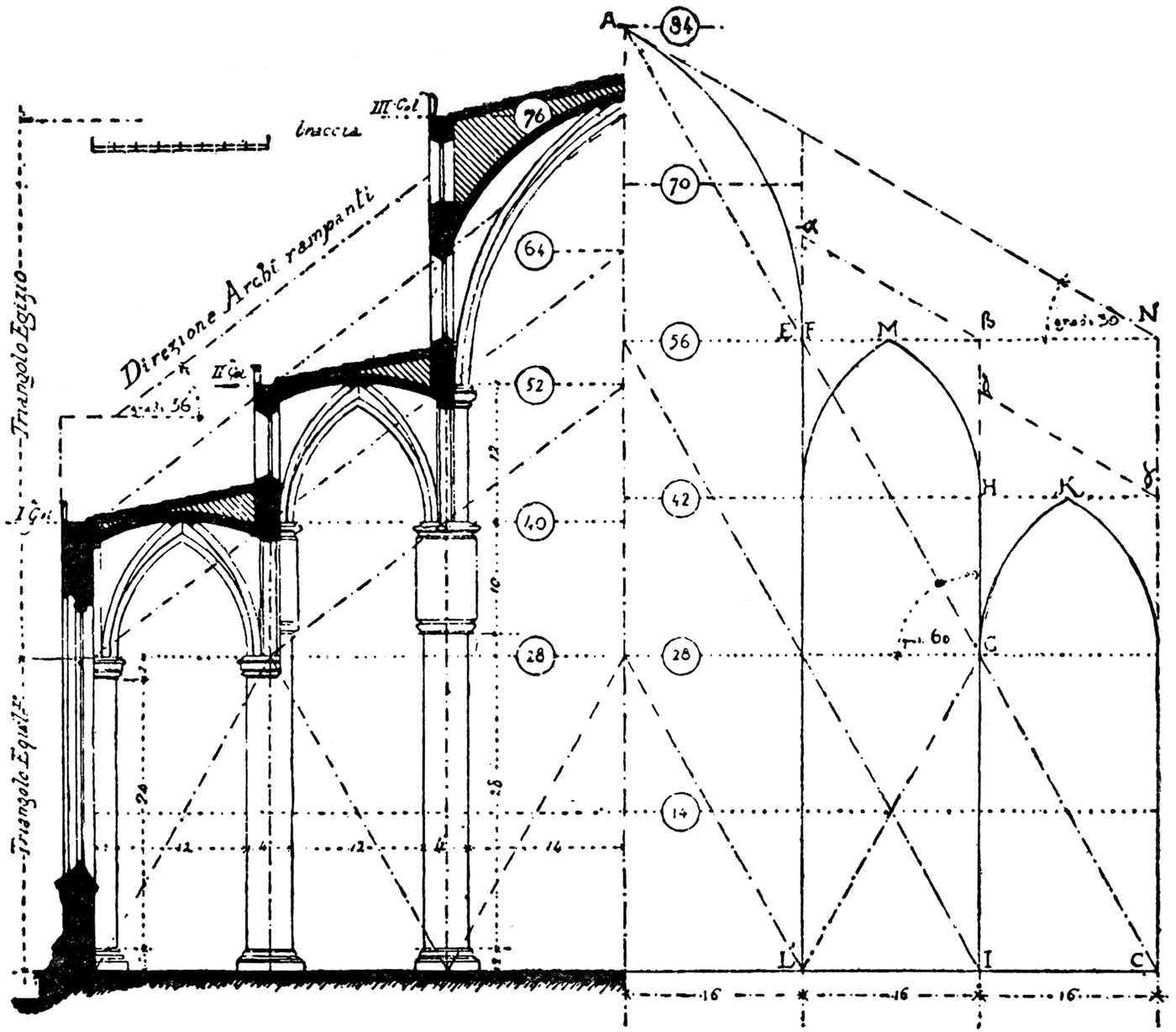
It was the greatest of all the experts on the history of Milan Cathedral, Luca Beltrami, who formulated the famous hypothesis that the master-builders had indeed abandoned Stornaloco's equilateral triangles with bases of 16 units and heights of 14, and had instead adopted a scheme based on Pythagorean triangles (which, after Viollet-le-Duc, he called ‘Egyptian’ triangles, and which have sides in the proportion of 3:4:5 that guarantee a right angle), rising from the imposts of the inner-aisle vaults (Fig. 7).Footnote 55 Beltrami proposed that a change from a height of 14 braccia to one of 12 braccia up to the imposts of the aisle vaults was determined by a wish to adopt such a triangular format, given that the ratio between a height of 12 braccia and a length dimension of 16 braccia is equal to one of 3:4.Footnote 56 This, he thought, was the change of plan that lowered the heights of the structure to those of the actual building, and fixed the inner-aisle imposts at 40 braccia (28 + 12), the imposts of the nave-vaults at 52 braccia (40 + 12) and the apex of the nave-vault at 76 braccia (52 + 24), rather than to the heights envisaged by Stornaloco I of 42, 56 and 84 braccia (Fig. 7).
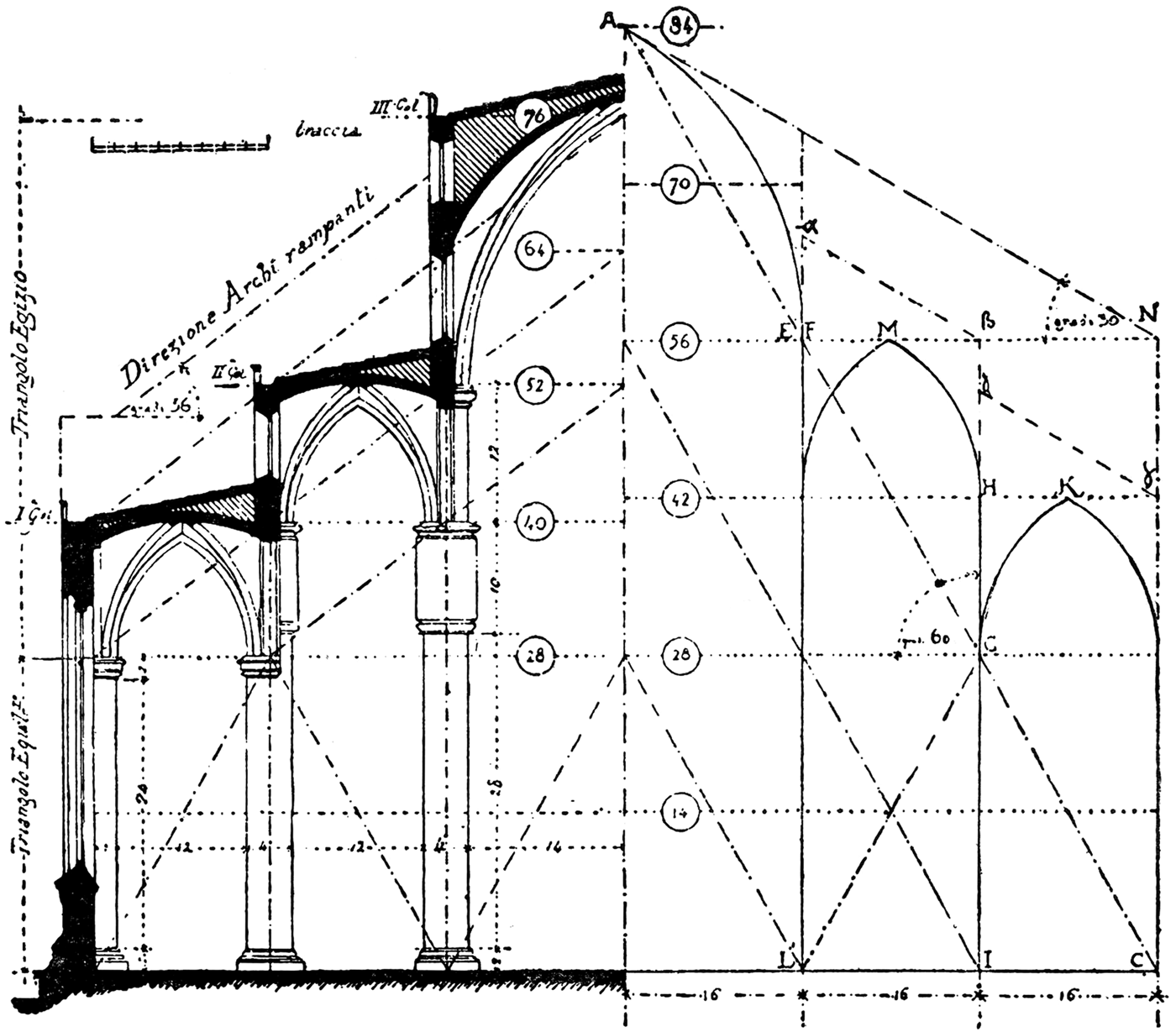
Fig. 7. Cross-section of Milan Cathedral as built, left, compared with Stornaloco's scheme, right (after Beltrami, ‘Il coronamento della fronte del Duomo di Milano’, 1900)
Beltrami's solution to the ‘problem’ of the reductions in height has generally been followed from Frankl onwards, and it was regarded by Ackerman as one of the many symptoms of the incompetence of Milanese masters in comparison with Northern architects (see Section 5). But the solution is far from convincing because it does not satisfy a fundamental requirement of the elevation of the project: the generation of the key points for constructing the ‘pointed-third’ vaults universally employed in Milan Cathedral. By contrast, Stornaloco's system based on equilateral triangles (and rectangles) allowed the architects to generate without difficulty the curvature employed for all the vaults in the cathedral, specifically described by Cesariano as being of ‘pointed third’ (terzo acuto) shape.Footnote 57 In fact, once the distance between the springing-points of the vaults of the nave and aisles was established, all the master-masons had to do in order to generate the required profiles for the vaults was to draw segments of two equal circles, each centred at the ends of the springing line of the vault and, using a radius equal to the span of the vault, make the segments intersect at the apex of the equilateral triangle. By contrast, Beltrami's Pythagorean triangles 12 braccia high do not permit the construction of pointed-third vaults, and, in fact, his hypothesis appears to rest on mistaken premises. The widths of the triangles that Beltrami proposed were generated by the interaxial distances between the piers (16 and 32 braccia), but their heights – to judge from his celebrated drawing (Fig. 7) – evidently refer to the intradoses of the vaults rather than their extradoses; and this is an error of logic since triangles based on interaxial distances should have heights corresponding to their extradoses and not their intradoses.Footnote 58
A much more convincing explanation of why the heights of the cathedral's actual vaults are lower than those envisaged by Stornaloco has recently been put forward by Giuseppe Valentini.Footnote 59 He has proposed that the cathedral builders did not actually abandon Stornaloco I in May 1392, but that, in order to maintain the curvature of the vaults that had been decided upon, they merely used Stornaloco's initial proposal (Stornaloco I) in a different way for good practical reasons, transforming it into the scheme which we call Stornaloco II.
The dimensions established by Stornaloco I for the heights of the vaults refer to their extradoses because, in his skeleton-scheme, the lines springing from the axes of the piers when extended upwards to form the vaults naturally described their extradoses.
Valentini's argument is that, while the interaxial distances between the aisle-piers is 16 braccia and those between the nave-piers is 32 braccia, the clear distance between aisle-piers is a little more than 14 braccia and that between nave-piers a little less than 28 braccia. What most likely happened, therefore, is that, when constructing the acute-third vaults above the piers and taking into account the breadths of the piers, it was more practical to measure to the intradoses, which corresponded to the positions of the form-work used for construction. According to the proportions of the equilateral triangles that generated the pointed-third vaults, the heights of the vaults at the intradoses were, therefore, slightly more than 12 braccia for both the aisles (the height of an equilateral triangle with base of 14 is about 12), and slightly less than 24 braccia for the nave-vault (the height of an equilateral triangle with base of 28 is about 24). It was on this basis that the executants established the heights of the imposts of the inner-aisles, which were based on the heights of the intradoses and not the extradoses of the outer-aisle vaults, and they then established the imposts of the nave-vaults using the intradoses and not the extradoses of the inner-aisle vaults, thereby losing two, four and eight braccia in height at each step with respect to Stornaloco I (Figs 7 and 9).Footnote 60 This resulted in the dimensions measurable today in the cathedral as built, which correspond with Stornaloco II with its principal heights of 28, 40 and 52 braccia, and with only a slight deviation from the 76 braccia for the nave vault, a problem to which we will return (Fig. 9). The question of the thicknesses of the vaults, and the consequent difference in height between the intradoses and extradoses compared with the Stornaloco I skeleton-like scheme, was not relevant when the masters were preparing to build the outer aisle-vaults, where they simply placed their formwork at the pre-established height of 28 braccia. But the question then emerged when they had to start building the inner-aisle vaults and this was the subject of the discussions of 1392, when they finally ratified the changes of dimensions incorporated in the second scheme, Stornaloco II.
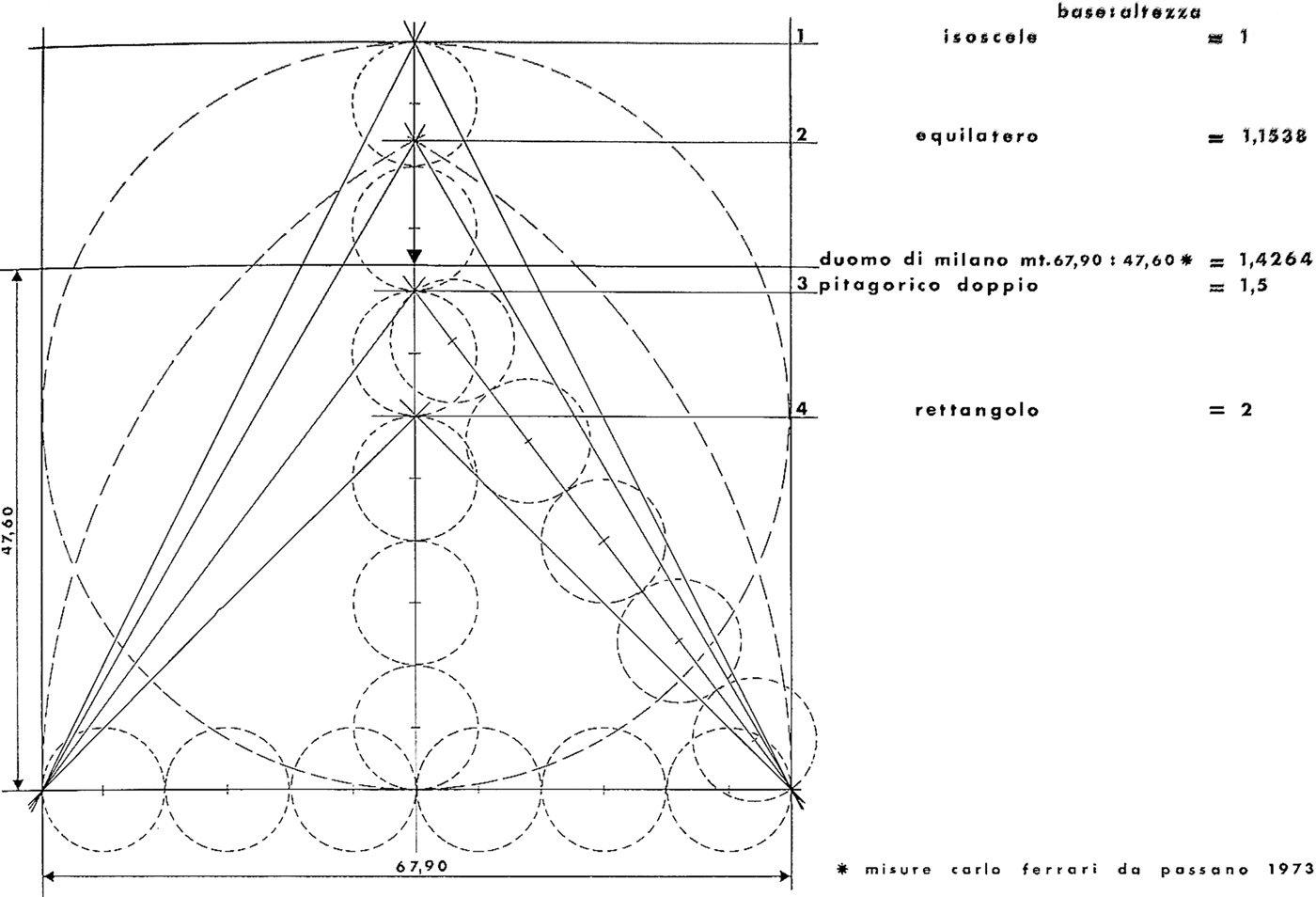
Fig. 8. The height of Milan Cathedral compared to an ad triangulum scheme and to one based on double Pythagorean triangles (after Verga, Il Duomo di Milano da Bramante-Cesariano a Stornaloco, 1980)
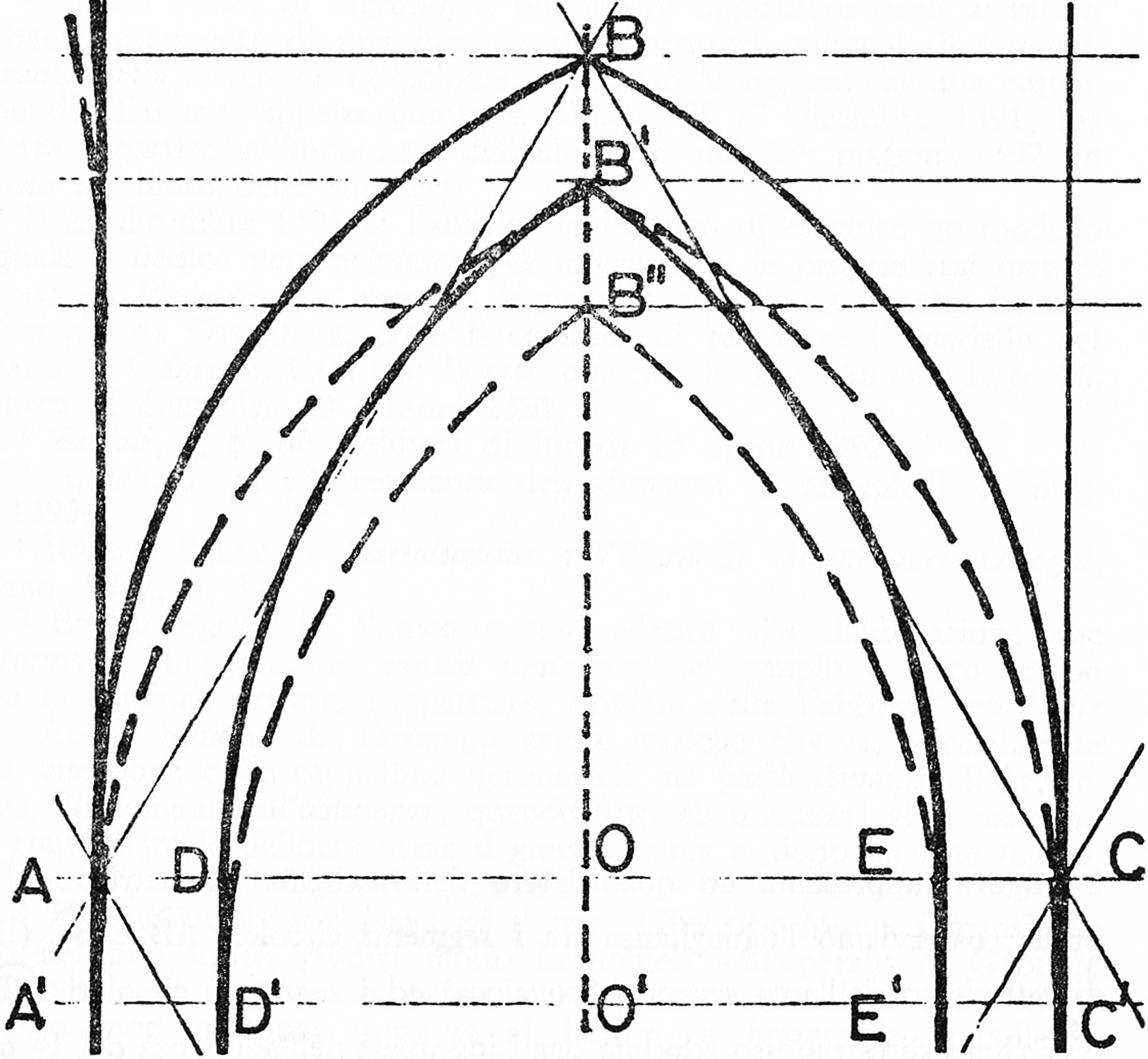
Fig. 9. Stornaloco I, above, compared to Stornaloco II (Valentini, Il duomo di Milano, 1990). Valentini's hypothesis is that the dimensions established by Stornaloco I for the heights of the vaults refer not to their intradoses but to their extradoses
However, when we examine modern surveys of the cathedral more closely (Tables 1 and 2), it appears that Valentini's limpid explanation, which in principle remains convincing, still requires some amendment.Footnote 61 First, Valentini assumed that the clear-distance between the piers was equal to the clear distance between the springing-points of the vaults, but this is not the case in practice. The clear distance between the nave-piers is about 28 braccia generating a height for the vault ad triangulum of 24 braccia, but the clear distance between the aisle-piers is about 12 braccia,Footnote 62 and not the 14 braccia indicated by Valentini, since the piers are all slightly broader than 4 braccia.Footnote 63 If we were to follow Valentini's hypothesis using the distances between the piers, the heights of the aisle-vaults generated by equilateral triangles would then be about 10 braccia, creating a sequence of dimensions of 28 braccia for the imposts of the outer aisle vaults, 38 braccia for the imposts of the inner aisle vaults, 48 braccia for the imposts of the nave-vaults, and 72 braccia for the nave vault – dimensions that have nothing to do with the cathedral as built. However, Valentini's explanation can be made workable if instead one considers the clear-space between the springing-points of the vaults and not the clear-space between the piers, because the springing-points are set back with respect to the vertical faces of the piers. Thus, the width between the springing-points of the vaults of the outer aisle is in fact about 14 braccia and the height is about 12 braccia, which creates heights for the imposts of 28, 40 and 52 braccia that are the same as those in the cathedral as built.
Table 1. The principal breadths of Milan Cathedral according to the Stornaloco I and Stornaloco II schemes compared with those given in modern surveys of the building. Dimensions in braccia in italics are converted from metres, but using decimals for convenience; dimensions in metres in italics are calculated from unannotated drawings.
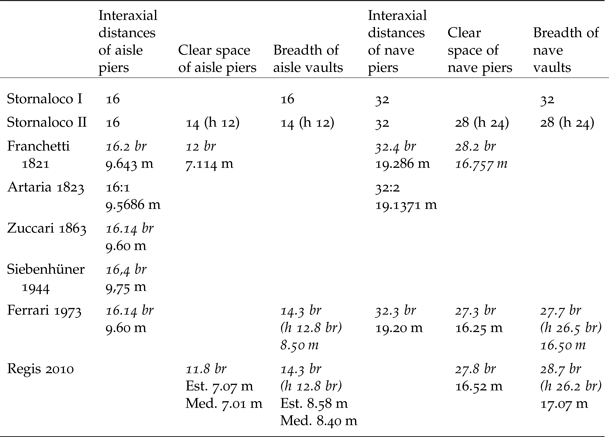
Table 2. Principal heights of Milan Cathedral according to the Stornaloco I and Stornaloco II schemes compared with those given in modern surveys of the building. Dimensions in braccia in italics are converted from metres, but using decimals for convenience; dimensions in metres in italics are calculated from unannotated drawings.
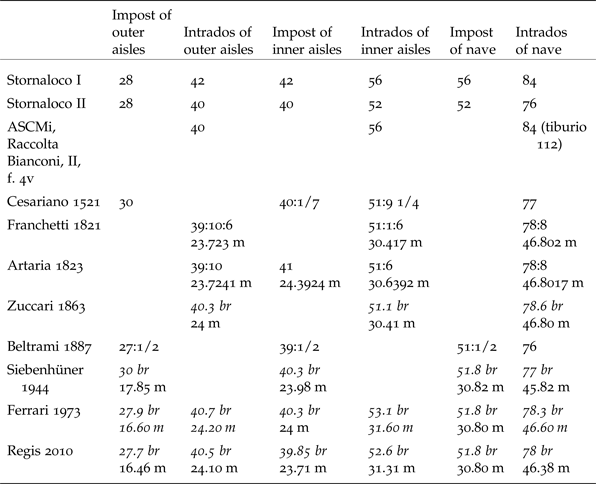
There is a further difficulty concerning the height of the nave-vaults. In this case the difference between the clear-space between the piers and that between the springing-points of the vaults is not particularly significant and both can be rounded up to 28 braccia. However, the total height of the intrados of the nave-vault as built ended up at around 78 braccia and not the 76 braccia predicted by Stornaloco II. The reason for this, however, is that the height of the vaults themselves ended up at around 26 rather than 24 braccia, resulting, therefore, in vaults that are slightly raised and not precisely ‘acute-thirds’. Thus the discrepancy between Stornaloco II and the cathedral as built is merely two braccia (1.2 m) with respect to the height of the intrados of the nave-vault.Footnote 64
Confirmation of Valentini's hypothesis that the architects developed Stornaloco II without abandoning the equilateral triangles enshrined in Stornaloco I is supplied by a passage of a well-known document recording the general meeting of 1 May 1392 (Appendix II, doc. I). This followed the nomination of Heinrich III Parler as Engineer of the Cathedral (appointed from December 1391 until July 1392),Footnote 65 and it was as a result of his criticisms of the recently accepted project (Stornaloco II), that the general meeting, with 35 Deputati and 14 engineers, was called. At the end of this meeting the new heights for the principal elements of the building were ratified, thus switching from Stornaloco I (28, 42, 56 and 84 braccia) to Stornaloco II (28, 40, 52 and 76 braccia). The passage in the document that confirms Valentini's hypothesis is the dubium (‘question’) number five, where it was asked (Appendix II, doc. I):
Q. What must the height in braccia be of the half-piers which will be built against the wall above the great piers themselves up to the vaults or arches to be built above them, and how high in braccia should the vaults be built above them?
A. They decided and announced that the half-piers should be 12 braccia high, and the vault of the nave itself should rise to the height of the triangle, that is 24 braccia. [Our italics]
In other words, the nave-vaults were to be constructed by using equilateral triangles with bases of 28 braccia, generating the height of 24 braccia specified in the minute, which means that those at the meeting were considering the clear-spaces between the piers, not the distances between the arches, or the interaxial distances between the piers, which would have produced a height of 28 braccia. The height of 24 braccia which they adopted was not described as having been generated by two units of 12 braccia (Beltrami's hypothesis) – nor by four ‘Great Units’ of 6 braccia (Frankl's idea) – but by the geometrical construction of the equilateral triangle, which allowed for the construction of ‘acute-third’ vaults.
Amongst the other questions posed in the same meeting was the much discussed third dubium which also confirms the hypothesis that the architects developed Stornaloco II without abandoning the equilateral triangles enshrined in Stornaloco I:
Q. Whether the church itself, not counting the tiburio in the dimensions, should ascend according to a rectangular or a triangular configuration?
A. They announced that it could rise as far as the [height of the] triangle or [‘sive’] triangular figure and no further. [Our italics]
It is important to point out, for clarity's sake, that the term sive (‘or’), is merely used as a reinforcing synonym (‘triangle or rather triangular figure’) as it is throughout the rest of the document, and not to distinguish different types of triangles as proposed by Frankl.Footnote 66 Thus the commission was asking itself whether the height of the church should derive from a system ad quadratum or from a system of equilateral triangles, and they decided on the second option. Frankl and Ackerman concluded from this passage that Parler, because he was opposed to the decision adopted at the meeting, had proposed an elevation for the Cathedral entirely ad quadratum, with modules of 16-by-16 braccia, which would have been simpler and would have involved rounding numbers up, but which would have resulted in a building too tall for the Italians.Footnote 67 But this hypothesis is flatly contradicted by a document of 1401 which informs us that Parler, like Annes of Freiburg before him (the engineer engaged from January to June 1391), had in fact proposed an elevation ad triangulum.Footnote 68 As the Deputato, Guidolo della Croce, stated (Appendix II, doc. III):Footnote 69
following the design begun later [that of Mignot], the erroneous system envisaged before [Stornaloco II] is changed and the correct triangular arrangement [Stornaloco I], from which one cannot depart without making errors, is followed, and which previously the aforementioned Master Enrico [Parler] and, of course, Master Annes the German before him had proposed loud and clear for the benefit of those who pretended to be deaf. [Our italics]
This document, therefore, indicates – contrary to the conclusions that have been reached by others previously – that Parler had raised objections to the decision of May 1392 to pass from Stornaloco I to Stornaloco II, and that, following Annes, he was a proponent of Stornaloco I; and it also shows that in 1401 Mignot agreed with them.
Further support for the hypothesis that in May 1392 the architects adopted the lower version of Stornaloco I, i.e. Stornaloco II, rather than a system of Pythagorean triangles, appears in a later document of 16 September 1410 when it was decided that the nave's arches, cross-vaults and cornices should be positioned immediately above the capitals of the half-columns attached to the side-walls, and not 4 braccia above them as the architect Cristoforo di Giona had wanted:
[It is decided that] the arches [crossing the nave], the cross-vaults and the cornices between the arches must begin from the capitals which have been built in the upper part of the nave, with the exception of the aforementioned master Cristoforo, who said that they should begin 4 braccia higher.Footnote 70
This, therefore, demonstrates that Stornaloco's scheme was still in play: the height at which the nave-vaults spring is 52 braccia in the cathedral as built, in accordance with Stornaloco II, but making the arches spring from 4 braccia higher would have made them arrive at 56 braccia, as required by Stornaloco I. The text continues by stating that the transverse arches and cornice must have a totum spigutum, a term which, by analogy with the expression a tutto sesto, probably denotes a curvature a tutto acuto, that is a pointed arch derived from an equilateral triangle like all the other vaults in the cathedral.Footnote 71 This is unlike the cross-vaults between the great arches that were to have a more convenient spigutum, i.e. a different although still pointed curvature.Footnote 72 The document then stipulates that:
these [transverse] arches should be 24 braccia high from the level of the capitals to the centre of that arch, that is, to under the key-stone of that arch; and these cross-vaults should reach to 26 braccia from the level of the capitals above to the key-stone of that cross-vault.Footnote 73
It therefore specifies that the great transverse arches should arrive at a height of 24 braccia at the apex of the intrados (subtus clavem: ‘under the key-stone’), while the cross-vaults should arrive at one of 26 braccia, that is with a slightly higher curvature, these being exactly the dimensions one finds in modern measured surveys, and thus confirming the adoption of Stornaloco II.
5. WORKING PRACTICE AT THE CATHEDRAL
The switch from Stornaloco I to Stornaloco II demonstrates the clear and precise thinking of the Milanese masters about the practical geometry and structure of their building. So is it true, as Ackerman believed,Footnote 74 that the rapid turnover of foreign and local master-builders at the cathedral was symptomatic of chaotic working-methods and widespread incompetence on the part of the Lombards?
In connection with the numerous directors of work at the cathedral and the many meetings arranged by the Deputati to resolve problems, Ackerman maintained that the first foreigner to be hired, the Frenchman Nicolas de Bonaventure, was invited in July 1389 reluctantly and only when it became clear that the Lombard masters were incapable of resolving the problems that had arisen.Footnote 75 Yet Bonaventure's work consisted mostly of designing decorative elements, such as the apse-windows, and we simply do not know if he was dismissed because, as Ackerman claims, he had raised structural and theoretical problems.Footnote 76 As for subsequent disruptions, Parler was dismissed in July 1392 for having caused ‘damage’ to the building and for his bad direction of the work, the precise nature of which is unspecified in the documents; so, although it was certainly connected with his objections to Stornaloco II (see Sections 4 and 8), there were many other grounds for disagreement.Footnote 77 When Mignot was summoned in April 1399Footnote 78 this was specifically as a substitute for two other architects, Giovannino de’ Grassi and Giacomo da Campione, who had died in July and October 1398 respectively.Footnote 79
It is true that the architects employed on the cathedral came from many different places, from Lombardy but also from Venice and the Ticino, and from the Rhineland, Bavaria, Paris, Normandy, the Low Countries and even Hungary, and it was precisely this that made the enterprise a centre of architectural research and international exchange. The sheer fame of such an ambitious project fascinated master-masons and artisans from all over Europe and it is easy to imagine that the Deputati wanted the very best on offer.Footnote 80 There were also cultural and political reasons for attracting experts from northern Europe in particular. French influence was strong on the Visconti court, given that in 1360 Gian Galeazzo Visconti had married Isabella di Valois, daughter of the King of France, and that in 1380 his daughter had married the king's brother. Again in 1380, Gian Galeazzo was granted the title of Vicario generale for Milan by the German emperor and, in 1395, that of Duke, thus reinforcing his connections with the German world too.Footnote 81
One factor in the undoubtedly slow place of decision-making, which emerges from the reports of the Deputati, is that nominated architects often worked together, rather than under one individual in overall charge, and that decisions were taken collectively. This, however, was in line with practices elsewhere in Italy. In Siena, during the thirteenth century, there were several commissions of expert builders who were appointed to decide on specific questions connected with the construction of the Cathedral, and – in 1274 – a permanent municipal commission for reviewing the accounts was established, of which six members were also Operaio advisors. The role of these members then increased in importance from the early fourteenth century, limiting the control of the Operaio and favouring a greater collegiality on matters of employment, finance and the choice and enactment of all works.Footnote 82 In Florence, the design-choices of the cathedral master-builder were strictly dependent on the Operai, and commissions, in part composed of experts, were often specially appointed to evaluate alternative proposals. Important decisions, moreover, were always submitted to commissions, which played a decisive role, and a system involving commissions composed of operai, master-builders, external experts, and ordinary citizens that held regular meetings, became standard administrative practice during the second half of the century.Footnote 83
Recourse to panels of experts was normal practice, in fact, with regard to many of the great Italian building-projects over successive centuries and in many different geographical areas.Footnote 84
Project administration at Milan and elsewhere was partly fashioned, too, on the model of the ‘disputes’ staged at mediaeval universities, to judge from the written form in which building debates were recorded, the disputatio or the established working-method of ‘disputing’ in order to find things out.Footnote 85 In respect to Milan Cathedral, therefore, we are not dealing with some peculiarity caused by the incompetence or uncertainty of the local Lombard architects, but rather with the standard practices that were established and administered by the Deputati.
Nor is it possible to claim that the presence of foreign master-builders was due to problems caused by the incompetence of the local Lombards who consequently turned to them. The alleged incapability of Lombards with respect to statics or structural mechanics by comparison with the Northerners is contradicted, for instance, by the fact that it was only when the French engineer Nicolas de Bonaventure had fallen out of favour with the Deputati that they decided (14 July 1390) to increase the sizes of the piers and foundations of the future cupola by three-quarters of a braccio because of the greater weight they would have to bear, and this immediately followed the appointment on 10 July of the Lombard Simone da Orsenigo in Bonaventure's place, and was well before the arrival, in December 1391, of another foreigner, Parler.Footnote 86
6. MIGNOT: ARS AND SCIENTIA
Ackerman's article investigates ‘the problem of Gothic theory and practice’ by analysing the published records of the cathedral.Footnote 87 In his view, ‘the history of the Cathedral is one of constant wrangling between [inadequate] local and foreign builders’.Footnote 88 The Lombards’ uncertainty had the further consequence, according to him, that ‘the section project seen by Antonio [di Vincenzo] was only the first of five different solutions’.Footnote 89 The Milanese, therefore, were ‘not moved by any conception of rational, causative relation among plan, section, and elevation’,Footnote 90 or in other words by any ‘theory’. And he found that the minutes of the meetings of 11 and 25 January 1400 (Appendix II, doc. II) were the ones in which ‘questions of theory play a major role’, revealing that the Milanese were ‘quite as deficient in practice as they are in theory’.Footnote 91 When interpreting these documents he understood the term scientia as ‘theory’, in the sense of ‘the higher learning in architecture’, or ‘abstract mathematical theory’, ‘higher geometrical principles’, ‘theory of consistent relationships’ and ‘ideal formulae’, a meaning that also included the structural mechanics of vault-thrusts.Footnote 92
But in the light of the arguments presented in Section 5 above, it seems necessary to return to the criticisms advanced by Mignot in December 1399 and January 1400, and to the often quoted – but not very well understood – statement of the Lombard engineers that ‘pointed arches do not direct thrust onto the piers’.Footnote 93 Rather than be shocked or bemused by this remark,Footnote 94 it is more useful to consider it in the circumstances in which it arose. Mignot's criticisms were presented in writing and at the repeated request of the Deputati,Footnote 95 as were the replies of the Lombard engineers, and the minutes of the meetings in which these criticisms were discussed, dated 11 and 25 January 1400 (Appendix II, doc. II), are carefully arranged according to a sequence in which each of his objections is followed immediately by the reply of the engineers, so that their points of view are clearly distinguished. These minutes, however, were compiled by notaries, along with the associated technical documents, and recorded in Latin,Footnote 96 a language which most of the engineers could not understand, and it is likely that some of the more technical details were not well expressed.Footnote 97 This is an important point to consider particularly where the written reports may seem obscure.
Passing to the contents of these reports, many of the criticisms Mignot expressed in the meeting of 11 January 1400 in various capituli or paragraphs are repetitive and clearly tendentious, and the engineers did not bother to reply to 29 of them because ‘they do not contribute substance and strength (quia non important [i.e. Mignot's capituli] substantiam neque fortitudinem), although it is not entirely clear whether the Lombards meant that Mignot's arguments had no substance and strength or, perhaps more likely, did not contribute anything useful to the dispute about the materials and the cathedral's structural stability.Footnote 98 In the second report of 25 January, Mignot added other, more general, observations which were still concerned with problems of statics (fortitudo) but were of more consequence (Appendix II, doc. II). He maintained, in his first observation, that the piers were not strong enough and should have been three times thicker, to which it was replied that they were strong enough because the stone used was much more resilient than French stone. It is Mignot's second point, however, that is the crucial one because this is where the term scientia makes an appearance. The term was given the broad meaning of ‘theory’ by Ackerman,Footnote 99 which has been generally followed in the literature, but this appears highly questionable. Throughout this whole section the term is clearly used only to refer to ‘geometry’, so that we find the expression scientia geometriae immediately followed by the terms scientia, scientia geometrica and then again scientia alone, and we should also note the apposition of the terms geometria and practica. With all this in mind, the passage assumes a different and maybe clearer meaning to that proposed by Ackerman, as the following paraphrase will indicate.
In the minutes, Mignot asserts that the four piers that will support the tiburio are not strong enough and will certainly collapse; and, further, he declares that the Lombards are ignorant (ygnorantes) when claiming that pointed arches are stronger than semicircular arches (which is true with regard to horizontal thrusts), and – worse still – that geometry (scientia geometriae) has no importance in this context since geometry (scientia) is one thing, and practical knowledge (ars) another. He then argues that practical knowledge (ars) without geometry (scientia) is worthless; that vaults, whether pointed or semicircular, are useless without good foundations;Footnote 100 and that, in any case, pointed vaults weigh more. The Lombards then reply by emphasising structural considerations, stating that the four piers are built on a square plan according to the principles of geometry (geometria); that it is untrue that they were additionally supported by the sacristies; and that they were soundly built of big blocks of stone tightly bound together with iron dowels, as they had already explained in the preceding minutes. They then add (Appendix II, doc. II):
that the weight of those three piers [a mistake for ‘four’] will be discharged equally onto the square perimeter [of the plan of the crossing] and they will be built vertically and strong, but [i.e. ‘and’] that which is vertical cannot collapse …
There will, therefore, be no eccentric thrusts outside the square formed by the four supports and the weight of the four piers of the crossing and of the tiburio above will discharge itself vertically so as to give the tiburio appropriate support.Footnote 101 Thus, when declaring that ‘pointed arches do not direct thrust onto the piers’,Footnote 102 the Lombard engineers were stating that pointed arches produced less horizontal thrust than semicircular arches, which is actually true and something the local engineers fully understood.Footnote 103
In a third argument, Mignot then insisted that the building would certainly collapse and that it was his duty to point out the defects. At this point, the engineers made use of Aristotle – very inaccurately – and argued that the church had been constructed ad triangulum, as had been established by other engineers, and that it had been designed, therefore, with ruler and compass (per rectam lineam, aut per sextum), i.e. with the use of straight lines and segments of circles for the geometrical construction of equilateral triangles and thus of the terzo acuto vaults. They concluded that what had been built had indeed been executed with both geometry (geometria) and practical knowledge (pratica), adding that Aristotle (not Mignot, as Ackerman and subsequent writers have claimed)Footnote 104 had said that geometry (scientia) is nothing without practical knowledge (ars) (Appendix II, doc. II).
It is in this context, therefore, that the Lombards stated that the science of geometry – no doubt referring to the use of perfect, regular figures such as the circle – is not relevant to such discussions since science, or rather geometry, is one thing and practice another (scientia geometriae non debet in iis locum habere eo quia scientia est unum et ars est aliud).Footnote 105
It was against this position that Mignot, not considering the static principles of the vaults, then made his now famous claim that practical knowledge without geometry is null (ars sine scientia nihil est). It thus becomes clear too that these two documents of 11 and 25 January 1400 (Appendix II, doc. II) were mostly concerned with stability and construction and the Lombard engineers correctly replied to Mignot's criticisms in terms of building practice; and this therefore undermines Ackerman's position on the matter. The questions defined by Ackerman as ‘theoretical’, or which suggest an opposition between the ‘theory’ and ‘practice’ of two opposed schools of thought, are merely part of the prescientific cultural baggage of the period, when statics or structural mechanics hardly existed as sciences. Instead, construction was validated by geometry, using elementary procedures which guaranteed a certain stability, coupled with a knowledge of local building techniques and materials.Footnote 106 In any event, Mignot certainly regarded their knowledge of geometry as defective simply because they were pursuing Stornaloco II and ignoring Stornaloco I.
7. THE SHEET OF DRAWINGS ATTRIBUTED TO ANTONIO DI VINCENZO
There remains one further important question: is the sheet of drawings usually attributed to Antonio di Vincenzo of any use for reconstructing the early cathedral projects? Modern-day writers are more-or-less agreed – and Angiola Maria Romanini in particular has dwelt on this pointFootnote 107 – that up till 1391/92 there was an initial project for an elevation ad quadratum, with a strong break between the nave and pairs of aisles of equal height. Then, according to this view (which is very different to the course of events proposed here), Stornaloco arrived and the authorities adopted a scheme of equilateral triangles. This was then changed – according to most scholars (see Section 4) – at the great conference of 1 May 1392 (Appendix II, doc. I) to a project based on Pythagorean triangles with a progressive rise of the aisles towards the centre creating a vast structure with three roofs per side, not two, which is the one that was actually built. The only source for the hypothesis that there was a project ad quadratum predating Stornaloco's arrival, however, is a free-hand drawing of the transverse section of the building which is almost invariably attributed to Antonio di Vincenzo from Bologna (Fig. 10).Footnote 108 The drawing, on a sheet which includes the plan of the cathedral and a view of one the sacristies on the verso, is usually dated 1390, before Stornaloco's arrival in Milan in 1391, on the basis of an alleged visit by Antonio to Milan to study the building in preparation for his vast project for S. Petronio in Bologna.

Fig. 10. Antonio di Vincenzo (attributed) or copyist, plan and cross-section of Milan Cathedral (Bologna, Archivio della Fabbriceria di S. Petronio; with permission)
The sheet was first published by Beltrami, who identified it as the earliest that we have of the cathedral. He dated it to 1390 partly because the plan on it shows the doors of the sacristies placed in the wrong position, that is, close to the piers of the crossing; and, in his reconstruction of events, these doors were then moved in 1391 to their present position, next to the wall-piers nearer the apse.Footnote 109 Beltrami's idea that the elevation drawing represents a project which predates that of Stornaloco of 1391 has remained the one universally accepted in the cathedral literature.Footnote 110
But what kind of elevation does the drawing show? Boito first suggested that it was ad quadratum with units of 16 (for the breadth) and 10 (for the height).Footnote 111 Frankl elaborated on this suggestion and selected certain dimensions marked on the diagram, but only those in tens (10, 30 and 40), and he also included dimensions of 50 and 60 units by adding together some of those specified on the drawing; and, to support his hypothesis, he proposed 90 units for the height of the nave vault. He thus suggested an elevation based on a module or ‘Great Unit’ of ten braccia for which he thought a yardstick of five braccia (3 m) could have been used on the building-site (Fig. 11).Footnote 112 This reconstruction has remained the one accepted by scholars including Ackerman who adopted this purely ‘utilitarian’ scheme based on dimensions of 10 units to reinforce his view that the project proceeded ‘haphazardly’.Footnote 113 Romanini,Footnote 114 followed by Antonio Cadei,Footnote 115 accepted that the scheme was devised ‘arithmetically’, and so too did Valerio Ascani.Footnote 116 But these hypotheses are highly problematic, and, instead, we will argue that the traditional date for the drawing is wrong and that the elevation does not show a scheme ad quadratum but is instead a flawed version of Stornaloco II, the adjusted version of Stornaloco I chosen on 1 May 1392.
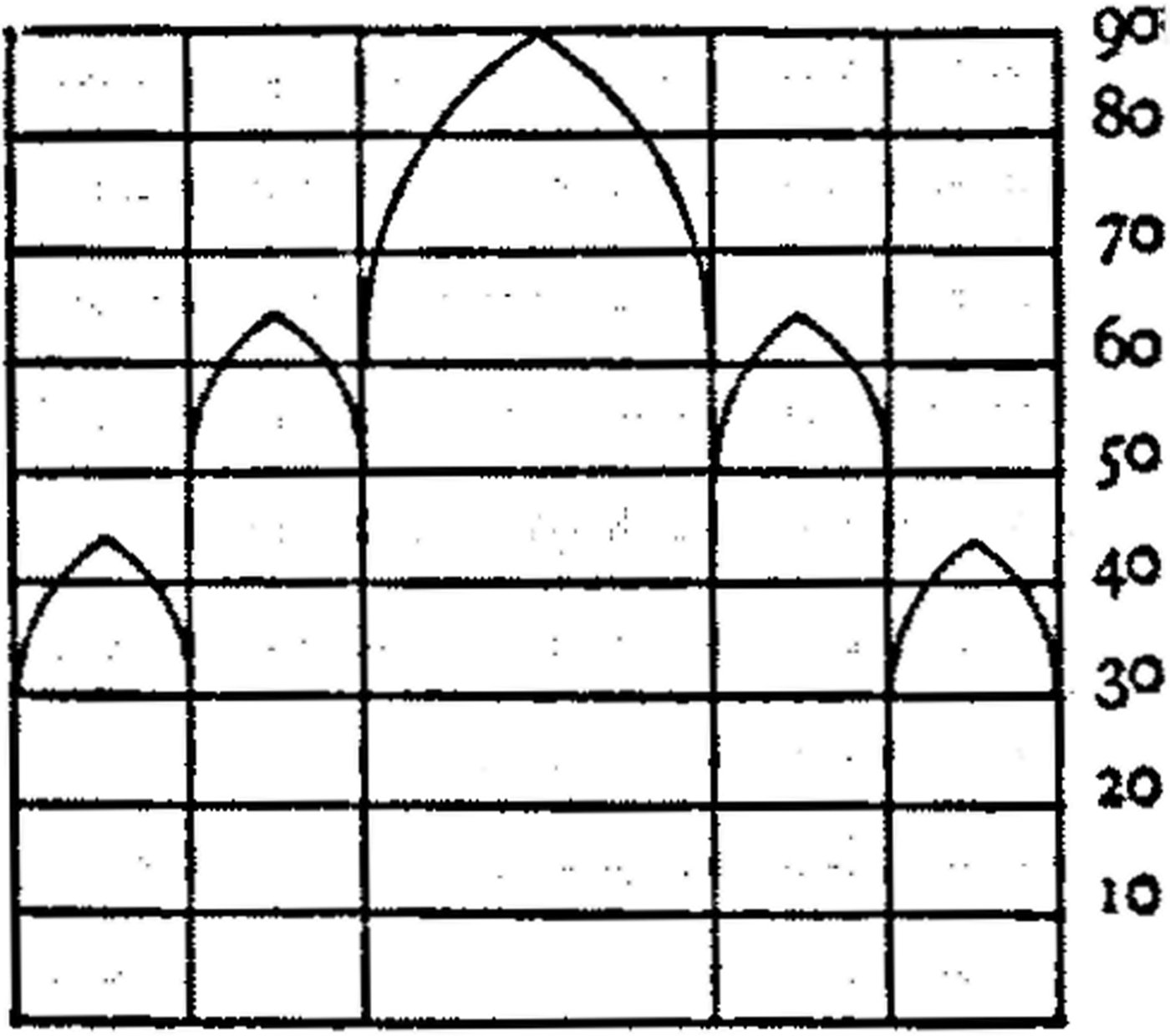
Fig. 11. Reconstruction of the cross-section of Milan Cathedral attributed to Antonio di Vincenzo based on Frankl's hypothesis (after Ackerman, ‘Ars sine scientia nihil est’, 1949)
As regards, first, the date of the drawing, medieval cathedral administrations kept meticulous records of when and why their chief architects left their building-sites. There is no evidence that Antonio di Vincenzo visited Milan in 1390; rather the administrators of S. Petronio recorded that he visited Milan Cathedral from 17 to 27 March 1393 with a famulus (servant), and then the cathedral in Florence for six days, from 30 March 1393, to recruit stone-masons for S. Petronio.Footnote 117 If our sheet of drawings is connected with the activities of Antonio di Vincenzo, then we must date it (or its sources) to March 1393 and this means that it comes after, not before, the revision of Stornaloco's scheme in May 1392.
As regards, secondly, the hypothesis that we are dealing with an elevation based on dimensions of 16-by-10 units, this becomes more and more improbable when we examine the actual dimensional annotations that are marked on the elevation drawing, which are as follows:
A [on the exterior aisle pier]: ‘braza XXX milanese piiando el capitelo’ (30 Milanese braccia including the capital)
B [on the inner aisle pier]: ‘braza XXXX perfino soto el capitelo’ (40 braccia up to below the capital)
C [the tabernacle capital of the inner aisle]: ‘braza X’ (10 braccia)
D [along the vault of the nave]: ‘braza X’, ‘b. III’, ‘b. VI’ (10 braccia, 3 braccia, 6 braccia)
E [bottom left]: ‘va alta la cupola del mezo braza C.XIII’ (the cupola in the middle goes up to 113 braccia’).
These are supplemented on the verso (Fig. 12) by the following inscription:
alteza di santa maria rotonda da roma/sie braza lxxvj milanexi / largeza de la dita sie braza lxxvj / alteza de san lorenzo da milano / sie braza lxxvi / largeza di detta chiexa sie braza otanta’ (the height of Santa Maria rotunda in Rome is 76 Milanese braccia / the breadth of the same is 76 braccia / the height of San Lorenzo is 76 braccia / the breadth of said church is 80 braccia).Footnote 118

Fig. 12. Antonio di Vincenzo (attributed) or copyist, external elevation of the sacristy of Milan Cathedral (verso of Fig. 10)
From this we can conclude the following. The requisite curvature of ‘pointed-third’ arches, used universally in the cathedral, cannot be generated using a grid of rectangles of 16-by-10 units, because these rectangles could have not matched the required heights; and, furthermore, measurements of 10 units are never mentioned in the cathedral's copious documentation, while the figures of 3 and 6 units, as well as that of 113 braccia used for the height of the tiburio, have nothing to do with a system based on 10.
The sequence of 10, 3 and 6 braccia, marked above the tabernacle-capitals above the central piers and separated by pen-strokes, corresponds pretty well to (i) the height of the shafts of the half-piers attached to the walls of the nave; (ii) the height of the capitals of those half-piers; and (iii) the height of the wall between the capitals and the upper windows. The number 113 mentioned for the height of the cupola is as close as could be to the dimension of 112 units, which was the figure decided on by Amadeo and Dolcebuono in 1490 when they announced the dimensions of their cupola;Footnote 119 and, in any case 113, or rather 112, is not a multiple of 10.Footnote 120 It is also of great importance that on the verso the heights of the vaults of the Pantheon in Rome and S. Lorenzo in Milan are recorded as 76 braccia. The mention of these heights would be inexplicable and irrelevant if they were not regarded as the same as that envisaged for the vault of the cathedral nave, which was, of course, 76 braccia according to Stornaloco II; and, again, 76 is not a multiple of 10.
The hypothesis that the elevation illustrates a scheme of dimensions of 16-by-10 units resulted mainly from a simple error (one among many) made by the draughtsman who placed the great tabernacle-capitals of 10 braccia in the wrong position, with the result that his elevation turns into nonsense when it arrives at the height of the nave-vault. As a result, he placed the capitals, 10 braccia high, on top of the piers of the inner aisles and nave, which he says are 40 braccia tall, so arriving at a height of 50 braccia. He then added the half-piers 10 braccia high attached to the inner faces of the nave walls above the great capitals, arriving at a height of 60 braccia for the nave-vault imposts.Footnote 121 But since the nave-vault was intended to reach 76 braccia, as indicated on the verso, it would have been impossible to construct a vault arriving at 76 braccia from a springing point of 60 braccia, because such a vault would be only 16 braccia high and could not be a ‘pointed-third’.
The true location of these key elements was specified on 1 May 1392 when they moved to Stornaloco II (Appendix II, doc. I). The document reads as follows:
Q. How many braccia high must the piers supporting the nave or the middle nave [ie. the inner aisle] be?
A. They announced that those piers, including the bases and capitals, should rise to 40 braccia and no further. [Our italics]
Q. How many braccia high should the minor piers or rather the piers of the chapels [i.e. those of the outer aisles] and the half-piers [i.e. those attached to the inner faces of the walls above the piers of the nave] rise, which, with the wall above them, should extend up to the arches aligned along the nave?
A. They replied and announced that those smaller piers [of the outer aisles] should be 28 braccia high; and that the half-piers [of the nave] to be built above them up to the arches should be 12 braccia high, including in those dimensions the bases and capitals’. [Our italics]
In other words, the height of the outer-aisle piers remains 28 braccia; the height of the inner-aisle and nave-piers should be 40 braccia, including the great capitals and bases; the half-piers attached to the walls above the nave-piers should arrive at 12 braccia (not the 10 + 3 indicated on our drawing), and this makes the height of the nave imposts 52 (40 + 12) braccia. It means that, if we restore the capitals in the drawing to their correct positions as part of the 40 braccia heights of the inner aisle- and nave-piers – or rather we restore what the written specifications should have said about them – then the springing-point of the nave-arches arrives at 52 braccia, not 60, and there is space for ‘pointed-third’ vaults of 24 braccia arriving at the apex of 76 braccia required by Stornaloco II and implied on the verso (Fig. 12, bottom right).Footnote 122
The conclusion, therefore, is that the elevation is an incompetent version of Stornaloco II, of which it reproduces the dimensions more or less accurately. The piers of the external aisles are indicated in the drawing as 30 braccia in height instead of 28 and the piers of the inner aisles at 40 braccia as in Stornaloco II; if the mistake of placing the capitals too high is corrected, then the nave-imposts arrive at 53 braccia (40 + 10 + 3) instead of 52; the height of the nave-vault is 76 braccia as in Stornaloco II; and the height of the tiburio is 113 braccia instead of 112. Thus, if all this is correct, then the drawing is of little value for reconstructing the history of the debates about the cathedral during the early 1390s.
What else can we say about this and the other drawings on the folio (Figs. 10 and 12)? The sheet is now in the archive of S. Petronio in Bologna but we know nothing of its movements before its arrival there. It bears a single watermark consisting of a circle surrounded by five petals of nearly equal size that do not overlap but meet where they touch the circle. Each petal is formed of just over three-quarters of the circumference of a circle with slight distortions and there is no other decoration (Fig. 13). The various repertories of watermarks cite no examples of five-petal flowers anywhere before 1413.Footnote 123 All the Italian examples date from 1413 to 1446 and all originate from Bergamo, Como, Milan, Pavia and Piacenza: none are recorded for Bologna. There is, therefore, a prima facie (although not a watertight) case for supposing that the drawings were made in the second or third decade of the Quattrocento. If this is correct, and bearing in mind that Antonio di Vincenzo died between April 1401 and September 1402,Footnote 124 then he cannot have been the author of our drawings.

Fig. 13. Antonio di Vincenzo (attributed) or copyist, plan and cross-section of Milan Cathedral (as Fig. 10): detail showing watermark
Above, we argued that the elevation drawing, or its source, reflects the Stornaloco II scheme adopted in May 1392. We should now ask, therefore, whether our drawings or their sources could in fact be dated to March 1393, when Antonio visited Milan, not least because the plan is marked up in Bolognese feet and the drawing is now in the S. Petronio archive.Footnote 125 The evidence of the watermark, however, is still disquieting, perhaps fatal, to attempts to date the drawings to the 1390s – as opposed to the sources on which they could have been based. And the fact that the elevation-drawing is marked up in Milanese braccia not Bolognese feet presents a further problem, although there is still a good chance that the drawings are all copies of others produced in the 1390s.
So does the history of the cathedral confirm or contradict a hypothesis that the sources for the drawings are perhaps dateable to March 1393 when Antonio di Vincenzo made his trip to Milan? With regard to the ground-plan, it is remarkable that, despite the presence of accurate written dimensions of the building itself, it includes some startling errors, in addition to that relating to the position of the sacristy doors. The arms of the transepts have three bays instead of two, and the author had also begun to draw two other bays at the west of the right transept but then crossed them out. With respect to the sacristy doors, their erroneous location in the drawing is almost certainly a simple mistake and not an indication that their locations were subsequently changed, as was suggested by Beltrami and Boito.Footnote 126 Their position had been established some time before 1390 when it was decided to ‘polish the marble sculptures of the doors of the sacristies’.Footnote 127 There is thus no reason to think that they and their sculptures were moved from one place to another, and they appear in their present positions on Cesariano's plan (Fig. 14), which derives from a drawing, now lost, dateable to before January 1394.Footnote 128 On the Bolognese drawing a door with a central pier or column is shown in the left transept, and the authorities discussed the designamentum (design) of such a door at the meeting of 1 May 1392 (Appendix II, doc. I), which was a year before Antonio's visit.Footnote 129 In addition, the four piers of the crossing are shown to be larger than the others, so the drawing's source must be dated to after the decision to enlarge those piers in 14 July 1390, so again before Antonio's visit.
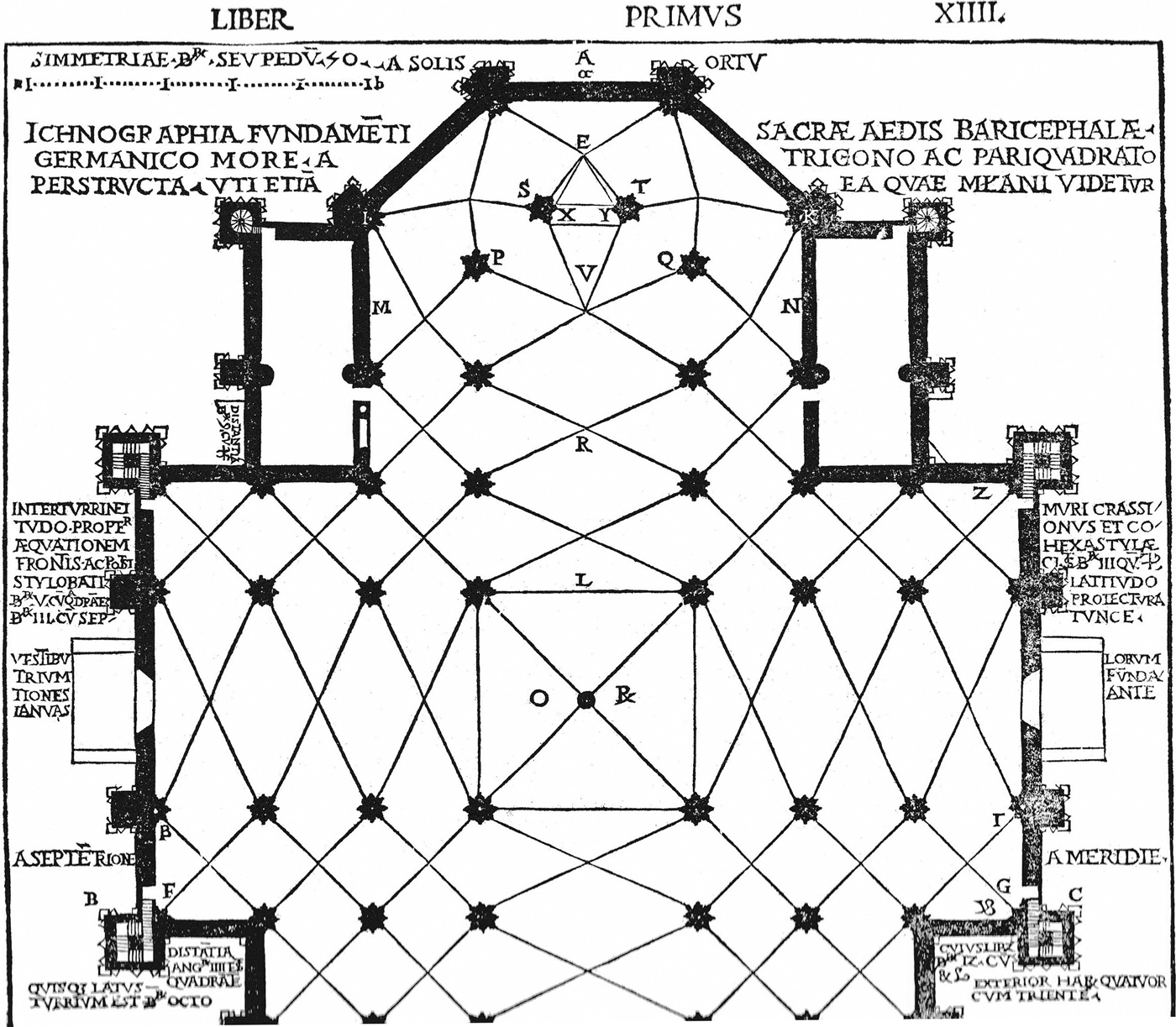
Fig. 14. Detail of ground-plan of Milan cathedral (from C. Cesariano, Di Lucio Vitruvio Pollione de Architectura, 1521, 14r). The plan, based on an older plan dateable to 1390–94, shows the reinforced piers below the cupola, the doors of the sacristies in their present positions and the sacristies without their vaults
The plan extends to the bottom of the sheet, presumably implying a nave of eight bays. It comprises 32 piers (or 34 if we include the extra bays wrongly added to the transepts). But the draughtsman also included measurements of some of the distances between the piers in the second bay of the inner aisle, away from the crossing in the direction of the façade; but he could not have measured the building itself as it was in 1393 because it had not yet reached as far as the nave and aisles. Apparently, by 1400 only 22 piers had been constructed and they comprised all those in the apse and transepts and two of the four at the junction of the transepts with the nave and aisles.Footnote 130 So it may well be that our architect was measuring a drawing or model of the building (conceivably that made under the supervision of Simone Cavagnera in 1392), not the actual building, and that he was then converting the dimensions into those of the building itself but using Bolognese piedi.
Finally, we may also have a terminus ante quem for the source of the drawing of the plan, because the sacristy vaults are not shown in the drawing, nor are they present in the plan published by Cesariano (Fig. 14). The decision to start building them came in January 1394, after Antonio's visit of March 1393,Footnote 131 so the source for our ground-plan, and for Cesariano's, must therefore be dated to before 1394. With respect to the source for the ground-plan, then, there appears to be nothing to prevent us dating it to 1393.
The elevation-drawing shows the great capitals 10 braccia high on top of the piers of the nave and inner aisles. Stornaloco would not have mentioned or drawn them, even if they had been designed and approved by September 1391, because his scheme was strictly skeleton-like. But in February 1392 (a month before Antonio's visit), Parler presented a wooden model for the capitals, this being the first documented mention of them.Footnote 132 From June 1393 to February 1396 various other drawings and life-size models of them were made and put in place,Footnote 133 and on 17 April 1396, when the archbishop had to decide which type of capital he wanted, he said that he liked those constructed in the form of ‘tabernacles with the intention of placing marble figures in them’. These capitals were evidently similar in form and height (10 braccia) to those seen in our drawing.Footnote 134 The conclusion from this is that, since our elevation drawing or its sources apparently date to 1393, then the general design of the great tabernacle-capitals, regarding their size and the fact that they should include niches with statuary, had already been established by Parler and perhaps others by February 1392.Footnote 135
The author of the elevation-drawing is certainly not reproducing an original drawing with the dimensions marked on it in Milanese braccia, since, if so, the inaccuracies with respect to the dimensions and the placement of the great capitals would be incomprehensible. One wonders, therefore, whether he was drawing the elevation from the Cavagnera model, illustrating Stornaloco I, which had been completed by May 1392; but after realising that the dimensions had been altered in accordance with Stornaloco II, either he, or perhaps his copyist, tried to indicate them with captions.
Finally, it is clear that the drawing on the verso (or its original) of the exterior of the North sacristy must be dated before 1403, because it shows the building before it was realised in its present form with the Carelli spire put in place in that year (Fig. 12).Footnote 136 All told, therefore, the information incorporated in this drawing, and in the plan and elevation does not preclude us from dating them or their sources to 1393.
But are we dealing with original drawings by Antonio di Vincenzo or with copies? If, notwithstanding the evidence of the watermark, the drawings now in Bologna were made at the cathedral in Milan in March 1393 by Antonio di Vincenzo, one the great architects of the late Trecento, who then took them back to Bologna, why do they include so many errors in plan and elevation and, above all, why do they use two systems of measurement? Unfortunately, we have no other drawings by Antonio, and the ones for the campanile of S. Francesco at Bologna (c. 1397) that were published as copies of his drawings are clearly early twentieth-century pastiches.Footnote 137 Perhaps, instead, we really are dealing with bad copies, made in the 1410s or 1420s for reasons unknown, of originals drawn by Antonio in Milan in 1393, and taken back by him to Bologna – perhaps drawings made by him on separate sheets which were then brought together on one sheet by a copyist. The handwriting, which appears to be the same on recto and verso, would then have been added when the copy was made in Bologna, while the dimensions on the plan could derive from measurements taken by Antonio himself using Bolognese piedi that were faithfully written out again by the copyist. But, in this scenario, the origin of the mistakes on the plan would still remain inexplicable as would the fact that no paper bearing the five-petal flower is recorded for Bologna from the 1410s or 1420s.
The problem with the elevation drawing is caused by the captions with their contradictory and nonsensical dimensions. Had Antonio made a drawing of the elevation without indicating dimensions and was it our hypothetical copyist who, with only a vague knowledge of Stornaloco II, added the captions with the mistakes we have noted? Yet the fact that the dimensions are reported in Milanese braccia would presumably tell us that the copyist was Milanese, not Bolognese,Footnote 138 so it may be that the solution to this Gordian Knot is that the drawings are all copies of original drawings made by different authors for different reasons in 1393 which were then concentrated on one sheet some 30 or 40 years later.
8. THE FIRST PROJECT
The hypothesis, then, of an initial project for the cathedral based on a module of 16-by-10 braccia, proposed by Frankl and others on the basis of the Bologna drawing, is unacceptable for the reasons given above, while a hypothetical project ad quadratum, based on a module of 16-by-16 units, which has been attributed to Parler, results from an erroneous deduction from the document of 1 May 1392 (Appendix II, doc. I). There is indeed a reference to an elevation ad quadratum in this document, but we can show that an ad triangulum project for the cathedral elevation existed before Stornaloco's intervention and remained valid thereafter.
It is also absolutely clear from the documents, especially from the minute of 15 May 1401 (Appendix II, doc. III), that Jean Mignot did not propose a new project, but a return to Stornaloco I as against Stornaloco II: the height of the nave, which he wanted to raise by 8 braccia, would have in fact arrived at 84 braccia as in Stornaloco I.Footnote 139 It is equally clear, too, that Mignot's project was identical to that of Parler, in that both of them wanted to revive Stornaloco I.Footnote 140 As we have seen, Guidolo Della Croce, with Giovanni Alcherio and Simone da Cavagnera, supported Mignot's position in the meeting of 15 May 1401 (Appendix II, doc. III), and on that occasion he said:
I am certain that one cannot build it more beautifully or more laudably, and that Mignot is a real master of geometry, since I find that his projects are very similar to those of the most excellent Master Enrico [Parler], whom we had here some time ago, as though sent to us by God, and whom we would have still, had we not expelled him.Footnote 141
The identity of Mignot and Parler's projects is confirmed by an extraordinary document of 20 December 1401 containing a ferociously vituperative denunciation of the dishonesty and incompetence of the Milanese architects, Marco da Carona and Antonio Paderno, who were enacting Stornaloco II, and of the fact that Parler and Mignot had been dismissed. Some citizens then exhorted the duke to establish an independent commission to weigh up the rival projects, none of which would make sense if Mignot's project was not identical to Parler's, in that both wanted to build according to Stornaloco I.Footnote 142 The document of 15 May 1401 (Appendix II, doc. III) also confirms that Parler's proposal was the same as that presented by Annes of Freiburg just before Stornaloco's arrival. Thus, to sum up, the first documented reference to a scheme ad triangulum is to that of Annes of Freiburg (engineer from January to June 1391), and this was then followed by Stornaloco's (October 1391), then by Parler's (engineer from December 1391 to July 1392), and then that of Mignot (engineer from October 1399 to October 1401). We therefore have a prima facie case for supposing that a system of equilateral triangles (and rectangles) had been developed by a German architect before Stornaloco, and that Annes of Freiburg, presumably identical to the ‘Anechino de Alamania’ who had made the lead model of the tiburio in 1387,Footnote 143 was presumably the first architect to propose the ad triangulum system for the elevation of the greatest Italian Gothic structure ever built.Footnote 144
Stornaloco's task in October 1392, therefore, was not to develop a new project, but to perfect, validate and verify one that already existed in the light of the science of geometry, and thereafter the authorities and architects never thought seriously of changing its general principles.Footnote 145 They continued following his scheme in the late Quattrocento as Stefano Dulcino testified;Footnote 146 in the Cinquecento it was re-elaborated in great detail by Cesare CesarianoFootnote 147 and remained the sine qua non of the studies of the cathedral conducted by Ambrogio Nava and Giuseppe Mongeri in the Nineteenth Century.Footnote 148 It was only with the arrival of Beltrami that anybody began to think that Stornaloco had played an ‘insignificant role’ with respect to the elevation and that his project had been abandoned.Footnote 149
When, finally, the discussions of the late 1480s – in which Leonardo da Vinci, Donato Bramante, Francesco di Giorgio Martini, Luca Fancelli and many others participated – culminated in a decisive meeting held in July 1490 in the presence of all the protagonists and with the participation of the duke himself, Stornaloco's scheme remained the foundation, never to be abandoned, on which the Lombard architects, Giovanni Antonio Amadeo and Giacomo Dolcebuono, with a contribution from Francesco di Giorgio, constructed the cathedral's great tiburio.Footnote 150
DIVISION OF AUTHORSHIP
Sections 1–6 and 8 and Appendix II were written by Giulia Ceriani Sebregondi; Section 7 and Appendix I were written by Richard Schofield.
APPENDIX I: STORNALOCO'S REPORT OF SEPTEMBER/OCTOBER 1391
One of the most important documents for the early history of Milan Cathedral, and the mainspring of the discussion presented above, is Stornaloco's letter and drawing made in late 1391. Stornaloco's original letter and drawing are lost and we have only a series of copies, but surprisingly there has hitherto been no attempt to establish exactly what the status of these copies is, or to produce a readable version of the letter.
1. THE COPIES OF STORNALOCO'S LOST TEXT AND DRAWING
Stornaloco's original diagram and report are lost, but we have three bad Nineteenth-Century transcriptions and two copies of the drawing. Nava (Memorie e documenti; Milan, 1854) transcribed the text which was then in the archive of the Milan Fabbrica del Duomo, and he made a tracing of the accompanying drawing in 1854, but his text is in part incomprehensible partly because of heavy damage to the original. Edoardo Mella (Elementi di architettura gotica da documenti antichi, Milan, 1863, fig. XIX, 3) made a copy of the drawing based on Nava's (Fig. 15), but without the text. Mongeri (‘Per la facciata del Duomo di Milano’, Il politecnico, 19, 1 –2 (1887), p. 102, note 1) transcribed the text again without much improvement, omitting the diagram. Beltrami (Per la facciata, Milan, 1887), used the document in the cathedral archive and an eighteenth-century copy in the library of Count Alessandro Melzi, which is also untraceable now, and he reports that the copy in the cathedral archive was a ‘copia sincrona’ of Stornaloco's original (p. 88, note 5). If both the cathedral and Melzi versions were copies, either or both may have included emendations or glosses. It is very curious that the cathedral copy of the report and drawing were not printed in the first volume of the Annali della Fabbrica del Duomo di Milano of 1877: they were certainly in the archive before and after that date when they were studied by both Mongeri and Beltrami.
Beltrami (Per la facciata, p. 73) also provided a free-hand version of Stornaloco's drawing (Fig. 16), but without specifying whether it was copied from the original in the cathedral archive or from the one in the Melzi library. It agrees with those of Nava and Mella in practically all respects, except that it places the letters ‘K’ and ‘H’ in their correct positions; and whereas Nava included a strip of Stornaloco's text down the right slope of the hexagon only, and Mella included some text on both slopes, Beltrami does not reproduce any text in these positions.
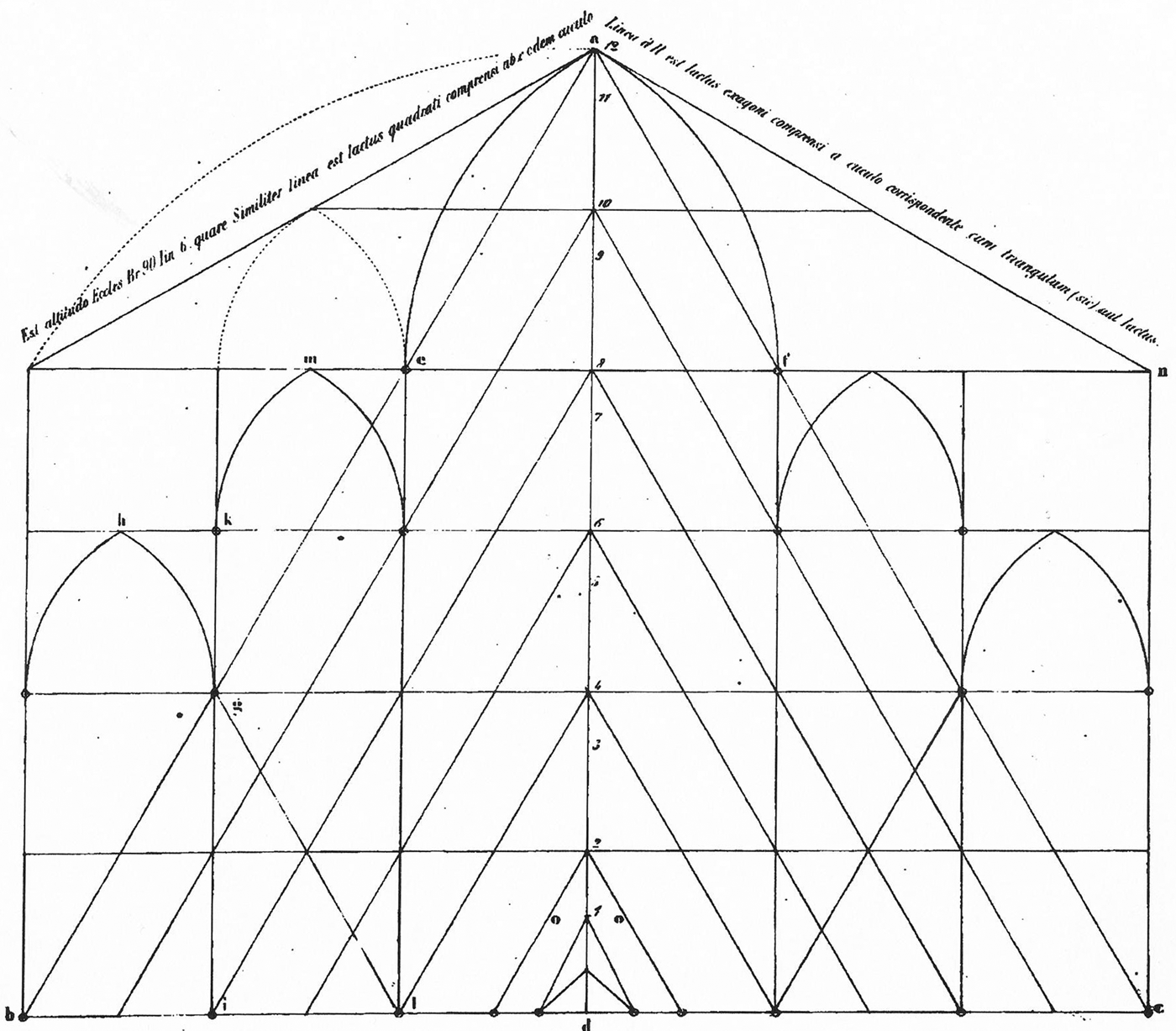
Fig. 15. Diagram based on Nava's copy of Stornaloco's drawing (after Mella, Elementi di architettura gotica da documenti antichi, 1863)

Fig. 16. Freehand version of Stornaloco's drawing (after Beltrami, ‘Per la facciata del Duomo di Milano’, 1887)
Nava and Mella indicate the key-points of the structure mentioned by Stornaloco in an elegant nineteenth-century lower-case script: they number the triangles up the axis AD with Hindu-Arabic numerals, and, curiously, do not space them out regularly, but bunch them together, 3 with 4, 5 with 6, 7 with 8 and so on. Beltrami spaces out the numbers of the triangles up the axis AD regularly and uses lower-case Roman, not Hindu-Arabic numerals, which may or may not have been the form used by Stornaloco: j, ij, iij, iiij, etc. Since Beltrami's drawing differs from Nava and Mella's with respect to the type of numbers employed (Roman not Hindu-Arabic) one wonders whether he was simply copying the cathedral version more faithfully than they were, or whether instead he was copying the Melzi version, which perhaps differed from the cathedral drawing in this respect.
2. THE RELIABILITY OF THE COPIES OF STORNALOCO'S DRAWING
The nineteenth-century copies of Stornaloco's diagram are incomplete. In Nava and Beltrami's versions (discounting Mella's as being a copy of Nava's), only parts of the circle and hexagon are illustrated, and none of the inscribed square, while the letter ‘O’ indicating the intersection of the square and the circle at the right is also missing. One suspects that the original drawing at the cathedral archive was itself incomplete in these respects, and so too, presumably, was the Melzi copy. These omissions were serious since the presence of these geometric figures was the mainspring of Stornaloco's project and the probable reason for his visit to Milan.
The drawings we have, then, are copies of incomplete versions of Stornaloco's original, and our nineteenth-century copies also include elements that were not mentioned by him in his text, which may be adjustments reflecting contemporary and later debates on the structure. These are as follows:
-
(i) Equilateral triangles are drawn at the right and left of the central axis by Nava and Mella, but only at the right of Beltrami's drawing. These triangles are based on the inter-axial distances between the nave-piers and the outer-aisle wall-piers and so replicate the fourth triangle on the central axis of the church (AD), to arrive at the height of the imposts of the outer aisles. These triangles may or may not have been present on Stornaloco's original.
-
(ii) A more substantial element that appears in the drawings, but is not mentioned in Stornaloco's text, is the extra vault drawn above that of the inner aisle at the left, of which the height is fixed by Stornaloco's tenth triangle, but in an arrangement that departs from that described in his text. The text requires that the differences in height between the vaults of the outer aisles and nave be expressed as thirds: the outer aisle-vault thus arrives at 42 braccia, the inner at 56 braccia and the nave at 84 braccia, so that the difference between the nave- and the inner vault (28 or ⅔) is twice that between the inner vault and the outer vault and (14 or ⅓). But the alternative shown at the top-left of our drawings presents a reversal of this relationship with the outer aisle vault at 42 braccia, the inner aisle vault now at 70 rather than 56 braccia, and the nave vault at 84 braccia: so the nave would now be only 14 braccia (or ⅓) higher than the inner-aisle vault, which in turn would be 28 braccia (or ⅔) higher than the outer vault.
-
(iii) In both versions of Stornaloco's diagram, an isosceles triangle is drawn inside the lowest equilateral triangle based on the primary unitas of 8 which Stornaloco does not mention and which is difficult to explain.
The situation, therefore, is desperate: our bad nineteenth-century transcriptions of Stornaloco's text and drawing are all based on copies, which makes resolving the most contentious and famous crux about calculating the heights of equilateral triangles particularly difficult.
3. THE TEXT OF STORNALOCO'S LETTER AND HIS METHOD OF CALCULATING THE HEIGHTS OF EQUILATERAL TRIANGLES
Stornaloco passes over his method of calculating the height of the triangles so rapidly that it was surely not something arcane, as Panofsky and Kidson claimed, but the reverse – something routine, known to everybody and thus not requiring extensive comment. He was addressing the cathedral Deputati, most of whom must have been highly educated, and to many of whom the formula will have been well-known; and Stornaloco states that the master-masons would understand his interaxial scheme and work out the clear spaces from it without difficulty (see Text, section 1).
The five transcriptions disagree chaotically. Here they are presented as they were printed by the authors:
‘Erit ergo linea a d que est altitudo sumitas eclexie radix de dec. 1020 sesanta 27, quia tregesima quod est aliquid minus de 84’ (Nava, Memorie e documenti, pp. 27–8);
‘Erit ergo linea a de quod est altitudo sumitas eclexie, radix de dec. 1020 60 27 (??) quia trigesimo quod est aliquid mimus de 84’ (Mongeri, ‘Per la facciata’, pp. 102–03);
‘Erit ergo linea A D, que est altitudo sumitatis eclexie radix dix dc dcc mxx sesara quie tregesime, quod est aliquid minus de LXXXIIII’ (Beltrami, ‘Per la facciata’, pp. 71 and 88 note 7);
‘Erit ergo linea AD que est altitudo sumitatis eclexie radix dc dcc mxx sesara XXVII [printed above ‘sesara’] quia tregesime, quod est aliquid minus de LXXXIIII’ (Frankl, ‘The Secret’, p. 53; and Panofsky, ‘An Explanation’, pp. 61–4);
‘Erit ergo linea AD, que est altitudo sumitatis eclexie radix de duc[tione] in XX sesnara [for ‘senaria’] quia tregesime’ (Beaujouan, ‘Calcul d'expert’, pp. 555 –63; idem, ‘Réflexions sur les rapports’, p. 444).
There is great uncertainty over what are numbers and what are words, which in any case were likely to have been abbreviated in some cases. The matter is complicated by the fact that Nava and Mongeri evidently changed what they thought were Roman numerals into Hindu-Arabic numerals, and presumably believed that the remaining lower-case letters in their transcriptions were not numbers but words or abbreviated words.
If we experiment by changing the Hindu-Arabic numerals in their texts to Roman numerals we can see that there is some agreement between Nava and Mongeri: ‘radix de dec. mxx lx xxvii quia tregesima’ (Nava) and ‘radix de dec. mxx lx xxvii (??) quia trigesimo’ (Mongeri); and these writers clearly did not believe that ‘de dec’ were numbers. But this is in conflict with Beltrami's version, aided by the Melzi copy: ‘radix dix dc dcc mxx sesara’, from which Beltrami extracted the figures 700 and 1020, leaving the initial ‘dix dc’ unaccounted for (although ‘dix’ in his transcription looks like a bizarre repetition of the end of the word ‘radix’, assuming it is not a number, and is absent from Nava and Mongeri's versions).
Panofsky's text, based on Beltrami's, is very misleading: he altered Beltrami's version, ‘radix dix dc dcc mxx sesara’ to ‘radix dc dcc mxx sesara’ from which he extracted the numbers 600, 700 and 1020, with XXVII printed above ‘sesara’; he derived the 27 not from Beltrami but presumably added it from Nava: worse still, he omitted Beltrami's ‘dix’, which could be 509 (if he was right that the following letters were numerals), and which, if included, would have interfered fatally with his explanation of Stornaloco's computations.
4. BEAUJOUAN'S HYPOTHESIS ABOUT STORNALOCO'S METHOD OF CALCULATION
Beaujouan's explanation is very attractive in principle because it involves a simple method, probably well-known to a number of the Deputati, and because it gives us a way of slicing through the chaos of the transcriptions. The strongest point in favour of his solution is his observation that ‘quia tregesim-’ emerges from all the transcriptions with only slight variations: ‘quia tregesima (Nava)’; ‘quia trigesimo (Mongeri)’: ‘quie tregesime (Beltrami; Panofsky)’, which surely tells that the altitude of the triangle, the ‘radix’, was calculated using thirtieths, and can therefore be connected with the formula 96 × (26 ÷ 30) = 83.2.
At the same time, Beaujouan suggested – brilliantly, even if he is wrong – that lurking in abbreviated form under ‘radix dc dcc’ (which Nava and Mongeri give as ‘radix de dec.’, and Beltrami as ‘radix dix dc dcc’) was the phrase ‘radix de duc.’, that is ‘radix de deductione in’ or ‘radix de ductu in’ for ‘multiplication by’.Footnote 1 This would explain perfectly how the number LXXXXVI was multiplied by 26/30 to arrive at the required height of less than 84.
Did Stornaloco express the formula 26/30 as Beaujouan suggests? Beaujouan accepted that XX in the letter-group ‘mxx’ was a number, but ignores the ‘m’, leaving XX for twenty. The presence in Nava's text of the Italian word ‘sesanta’, which becomes ‘60’ in Mongeri's (presumably reflecting what they believed to have been ‘sexaginta’), and the incomprehensible ‘sesara’ in Beltrami's and Panofsky's, prompts the thought that, at any rate, we need a word beginning with ‘se…’ straight after what appears to be XX. Beaujouan was struck by the presence of the number XXVII in Beltrami's text, not knowing that its appearance there above ‘sesara’ was an invention of Panofsky's or that it was present in Nava's and Mongeri's transcriptions in Hindu-Arabic form immediately before ‘quia tregesime’. Beaujouan proposed that the text originally read ‘XX sesnara’, a mistake for ‘senaria’, and that this mistake prompted the erroneous gloss ‘XXVII’ (a mistake for XXVI) recorded in the transcriptions. Panofsky prints ‘XXVII’ above the nonsense word ‘sesara’ which he wants to change to ‘sesquialtera’.
But there are obvious difficulties with Beaujouan's proposal that the original read ‘XX sesnara’. First, even if ‘sesnara’ were a lapsus calami for ‘senaria’ (by Stornaloco or the early copyists) as Beajouan suggests, why would anyone mistake it for XXVII? That would imply a bad paleographer with no knowledge of Stornaloco's formula 26/30; and, secondly, would Stornaloco have used a Roman numeral, XX, combined with a written version of the number six (‘senaria’), instead of writing XXVJ as elsewhere in the document.
Whilst accepting Beaujouan's explanation in principle, the simplest possible solution has been adopted in the text below as a stop-gap until someone thinks of something better. It does not account well for ‘sesanta-60-sesara’, but does provide a word beginning with ‘se-’, even though, admittedly, no other number in the document is given in both verbal and numerical form.
5. STORNALOCO'S LETTER: TEXT
Linea AN est lactus exagoni comprensi a circulo comprendente etiam triangulum cujus lactus est latitudo eclexiae, scilicet LXXXXVJ quantitatum: similiter linea AO est lactus quadrati comprensi ab eodem circhulo.
Bassis trianguli est linea BC et est latitudo eclexie, scilicet LXXXXVJ quantitatum.
Erit ergo linea AD, que est altitudo sumitatis eclexie,Footnote 2 radix de ductioneFootnote 3 in viginti sexFootnote 4 sive XXVJ, quia tregesime, quod est aliquid minus de LXXXIIIJ; quam divisi in sex partes in figuris triangularibus ac etiam in figuris quadrangularibus, prout patet in corpore majori eclexie; et trianguli incipiunt ab unitate secondum naturam triangulorum.
Quoniam unitas, cum fuerit posita,Footnote 5 est triangulus in potentia, et cum adiderimus super ipsam ij [unitates],Footnote 6 erit primus triangulus in actu. Et hoc modo crescunt trianguli in infinitumFootnote 7 et in figura suprascripta crescuntFootnote 8 usque ad duodecimum dividendo lactitudinem in XIJ partes prout evidenter patet.Footnote 9
Qui quidem trianguli omnes sunt equalium lactuum et equalium angulorum, sed quadrati sunt majores in basse quam in lactere [altitudinis?]Footnote 10 secundum diferentiam AD et BC:Footnote 11 preterea quia omnis linea perpendicularisFootnote 12 demonstrat se esse minoremFootnote 13 secundum quantitatem suam quam linea posita in base, ut linea AD que non multum videtur differre a lineaFootnote 14 BC, quamvis sint differentes ut supra.Footnote 15
Competens altitudo est secundum distantiam centri ad centrum colonarum, quiaFootnote 16 in lactitudine majori est XXXIJ quantitatum;Footnote 17 quidem colone ascendunt usque ad sumitatem quarti quadrati et basem [sic] octavi trianguli in angulis E et F,Footnote 18 et linea E et B secatur per medium in pontoFootnote 19 G quod est altitudo minorum colonarum;Footnote 20 mediane vero colone ascendunt usque ad angulumFootnote 21 H;
et primi corporis lactitudo,Footnote 22 que est BI, ascendit usque ad pontum K; secondi [sc. corporis lactitudo], quod est IL, ascendit usque ad pontum M, non secundum veram proportionem, quia equales sunt in lactitudine ergo deberent esse equales in altitudine, sed ponendo [?]Footnote 23 minorem [sc. corporem] cum majoreFootnote 24 qui est duplum minoris lactitudinis;Footnote 25
sequitur ergo quod excedit ipsumFootnote 26 proportionaliter in altitudine in ponto A; et mediana altitudoFootnote 27 excedit primam in tertiam partem ipsius;Footnote 28
sequitur ita quod major debet excedere medianam in duplum eius quod exceditFootnote 29 primam, quoniam in lactitudine est dupla ad ipsam, prout patet in figuratione, quia altitudo AM duplumFootnote 30 est altitudinis MK.
Omnes lactitudines acepi mensuratione centri ad centrum, ideo non curavi in designamento ponere spissitudinem colonarum quia satis est manifestum magistris inzigneriis quantum occupant in corporibus ecclesie, nec non lactitudine et area multa quidem possunt describi in numeris omnium corporum designatorum prout se habent secundum figuras geometricales, sed dimito causa prolixitatis.
Et hanc reverentiis vestris transmitto ordinatamFootnote 31 prout melius mihi possibilitasFootnote 32 est. Supplicans quatenus dignemini suportare quod erratum conffusumque fuerit, quia Deo teste si melius scirem cordialiter adimplerem.
6. STORNALOCO'S LETTER: TRANSLATION
The line AN is the side of a hexagon circumscribed by a circle which in turn circumscribes the triangle of which the side is the width of the church, i.e. 96 quantitates: similarly the line AO is the side of the square circumscribed by the same circle.
The base of the triangle is the line BC and this is the width of the church, i.e. 96 quantitates.
Therefore, the line AD, which is the height of the summit of the church, will be the square root resulting from multiplying [the base of 96 quantitates] by twenty-six or 26, since they are thirtieths, which is something less than 84; this [the line AD] I have subdivided into six parts with triangular and also rectangular figures as can be seen in the major body [the nave] of the church; and the triangles begin from a unit according to the nature of triangles.
For once the unit has been established, it is a potential triangle, and when we have added two [more units] above it, it will be the first actual triangle. And this is the way triangles grow infinitely: and in the drawing presented above they increase up to 12 dividing the width into 12 parts, as is absolutely clear [from the diagram].
In fact all these triangles have equal sides and angles; but the rectangles are wider at the base than their sides are high, in accordance with the difference between AD and BC, also because every vertical line is demonstrably shorter according to its quantitas than the line placed at the base, as is the case with the line AD which does not appear to differ much from the line BC, although they are different, as [shown] above.
The required height is established by the distance between the axes of the piers, because the greatest width [that of the central nave] is 32 quantitates: the piers [of the nave], in fact, rise to the top of the fourth rectangle and to the base [sic: apex] of the eighth triangle at the angles E and F; and the line EB is intersected in the middle at point G which is the height of the [imposts of the] minor piers; the intermediate piers in fact rise to the angle H.
And the width of the first body [the outer aisle], which is BI, ascends to point K; that of the second body [the inner aisle], which is IL, ascends to point M, not according to the true proportions, since they [the two aisles] are equal in width and should therefore be equal in height, but by comparing [?] the minor body [the outer aisle] to the major [the nave], which is twice the width of the minor.
Thus it follows that it [the nave] exceeds it [the inner aisle] in height in terms of proportions at point A, and the intermediate height [of the inner aisle] exceeds the first [the height of the outer aisles] by one third of the latter.
Thus it follows that the [height of the] nave must exceed the intermediate height [of the middle aisle] by twice as much as it [the height of the middle aisle] exceeds the height of the first one [of the outer aisle], because it [the nave] is twice as wide as it [the minor aisle]; as is evident from the drawing, since the height AM is double the height MK.
I have taken all the widths by measuring from axis to axis, so I have not bothered to set down the thickness of the piers in the drawing because it is sufficiently clear to the master-builders how much space they occupy in the bodies of the church; furthermore, with respect to the width and the area, a great deal could be quantified numerically as to how all the bodies represented in the drawing are related according to the geometrical constructions, but I omit this on account of its length.
And I submit this [letter] organized to the best of my ability to your Reverences.
I entreat you to deign to be patient with what may be mistaken or confused, for, as God is my witness, if I knew how to do things better, I would act accordingly with all my heart.
APPENDIX II: OTHER IMPORTANT DOCUMENTS
The transcriptions presented below are taken from Annali del Duomo di Milano. Some had already been published in whole or part by Nava (see below). The documents are in what is left of the Ordinazioni capitolari, vol. I, which covers the period 1390–1444. This volume was taken to an exhibition in Turin in 1906, where it was burnt and then soaked in water. Back in Milan, the archivists, with monumental patience, separated and photographed all the pages: the photographs can now be consulted at the Archivio della Fabbrica del Duomo. In some cases the pages are very damaged and next to invisible; however, both Nava and the transcribers who worked for the Annali are highly dependable.
Doc. I: 1392, 1 May
(Nava, Memorie e documenti, pp. 32–33; Annali, I, pp. 68–69)
The engineers discuss the configuration of the section of the Cathedral with particular reference to whether it should be built following a scheme of rectangles or triangles; they adopt a lower version (Stornaloco II) of that originally presented by Stornaloco (Stornaloco I).
Coll'intervento di tutti gli ingegneri sottonominati – maestri Giovanni da Ferrara, Zanello da Binasco, Stefano Magatto, Bernardo da Venezia, Giovannino de’ Grassi, Giacomo da Campione, Simone da Orsenigo, Pietro de’ Villa, Enrico da Gamondia (qui non consensit), Lorenzo degli Spazii, Guarnerio da Sirtori, Ambrogio da Melzo, Pietro da Cremona, Paolo degli Osnago.
Omnes congregati in camera fabricae ecclesiae mediolanensis pro tollendis pluribus dubiis quae moventur super fabrica ipsius ecclesiae, quae dubia inferius distincte specificantur, et juxta ipsa dubia factae sunt responsiones et declarationes per omnes ipsos inzignerios; excepto ipso magistro Henricho, qui quamvis responsiones ipsae suae sint datae ad intelligendum, ipsis declarationibus nullatenus consensit.
[…]
D. Utrum ipsa ecclesia debeat pluere in duobus tectiis an in pluribus, proportionabiliter fiendis ab utraque parte usque ad croxeriam?
R. Declaraverunt quod ipsa ecclesia debet et habet pluere pro majori fortitudine et claritate in tribus tectis et non in duobus.
D. Utrum ecclesia ipsa non computando in mensura tiborium fiendum debeat ascendere ad quadratum an ad triangulum?
R. Declaraverunt quod ipsa posset ascendere usque ad triangulum sive usque ad figuram triangullarem et non ultra.
D. Quot brachia debent fieri pilloni servientes navi majori sive navi de medio?
R. Declaraverunt quod ipsi pilloni computando bases et capitellos debent ascendere brachia quadraginta et non ultra.
D. Quot brachia debent ascendere medii pilloni qui in muro fient super ipsis pillonis magnis usque ad volturas sive archus superinde fiendos, et quot brachiorum debent esse volturae super ipsis fiendae?
R. Deliberaverunt et declaraverunt quod medii pilloni sint brachiorum duodecim, et voltura ipsius majoris navis ascendat ad triangulum, videlicet brachia vigintiquatuor.
D. Quid sibi videatur de designamento unius portae gemellae croxeriae versus Compedum cum tota facie ipsius croxeriae?
R. Ea visa et perspecta declaraverunt quod ipsa est valde pulchra et bona ac honorabilis, et quod super ea procedatur.
[….]
D. Quot brachia debent ascendere pilloni minores sive pilloni capellarum et medii pilloni, qui cum muro super eis fieri debent usque ad archus respondentes versus navem magnam?
R. Responderunt et declaraverunt quod illi minores pilloni debent esse alti brachia 28, et medii pilloni super eis construendi usque ad archus sint et esse debeant brachiorum 12, computatis in ipsis mensuris bases et capitellos.
Doc. II: 1400, 25 January
(Nava, Memorie e documenti, pp. 94 –96; Annali, I pp. 209 –10)
The celebrated debate in which Jean Mignot attacks the Lombard architects. He maintains that the piers they have built will not stand, particularly those of the crossing; and he accuses them of lacking, in effect, both practical ability (‘ars’) and a knowledge of geometry (‘scientia’).
Magister Johannes Mignotius de Parisiis dixit in consilio praesenti dedisse in scriptis usque nunc computata caedula per eum data in consilio praedicto omnes rationes et omnia motiva per quae vult dicere praedicta opera non habere fortitudinem et alias rationes non velle dicere.
Capitula ultimata data per suprascriptum magistrum Johannem de die 25 januarii.
1. Vobis egregiis dominis de consilio fabricae ecclesiae Mediolani cum reverentia et pura veritate significat magister Johannes Mignotius quod, sicut alias et inter alios defectus dictae ecclesiae exhibuit in scriptis, iterato dicit et proponit quod omnes contrafortes circum circha dictam ecclesiam non sunt fortes nec habiles ad sustinendum onus quod eis incumbet quia debent esse tribus vicibus pro quolibet grossis quantum est grossus unus pilonus de intus ecclesiam.
Magistri respondent: Supra primo capitulo dicunt quod omnes contrafortes dictae ecclesiae sunt fortes et habiles ad sustinendum suum onus et plus multis rationibus quia unus brachius nostri marmoris et sarizii in quolibet latere est tam fortis sicut brachia duo lapidum Franziae vel ecclesiae Franziae quam dat in exemplum suprascriptis magistris. Qui inde dicunt quod si sunt et sunt totidem et medium quotidem sunt piloni intus ecclesiam praedictos contrafortes esse fortes et esse ad suam rationem, et si fuissent majores obscurassent ecclesiam praedictam obstantem, videlicet ecclesia Parisiis, et quae habet contrafortes ad modum magistri Johannis et aliae rationes quia nocuisse possunt.
2. Item dicit [Mignot] quod quatuor turres sunt incoeptae pro sustinendo tiburium dictae ecclesiae et non adsunt piloni nec aliud fundamentum habiles pro sustinendo dictas turres, imo si ecclesia esset facta in toto illico cum dictis turribus infalibiliter rueret, super iis vero quod certe per passiones factae sunt per aliquos ygnorantes allegantes quod voltae acutae sunt plus fortes et cum minori onere quam voltae retondae, et plus super aliis propositum est ad voluntatem quam per viam virtutis; et quod est deterius oppositum est [by the Lombard masters] quod scientia geometriae non debet in iis locum habere eo quia scientia est unum et ars est aliud.
Dictus magister Johannes dicit quod ars sine scientia nihil est, et quod sive voltae sint acutae sive retondae non habendo fundamentum bonum nihil sunt, et nihilominus quamvis sint acutae habent maximum onus et pondus.
Item dicunt [the Lombard masters] quod turres quos dixerunt sibi velle facere dicunt pluribus rationibus et causis, videlicet, primo pro retificando praedictam ecclesiam et croxeriam quod respondent ad quatrangulum secundum ordinem geometriae; alia vero pro fortitudine et pulchritudine tiborii, videlicet quasi per istum exemplum in paradixo Dominus Deus sedet in medio troni, circha tronum sunt quatuor evangelistae secundum Apocalissim, et istae sunt rationes quare sunt incoeptae. Et quamvis non sint fundati duo piloni pro qualibet sacrastia incipiendo super terram, ecclesia est tamen fortis bene istis rationibus, quia reprexae super quibus dicti duo piloni et praedictae reprexae sunt de magnis lapidibus et inclavatis cum clavibus ferri sicut dictum est supra cum aliis capitulis, et quod pondus dictis tribus turribus ponderat [sic: read ‘ponderit’ to match ‘erunt’ below] ubique super suum quadrum, et erunt aedificatae recte et fortiter, sed [sic: ‘et’] rectum non potest cadere; unde dicunt quod sunt fortes per se et ergo dabunt fortitudinem tiborio, quia clausus est in medio illarum turrium unde dicta ecclesia bene fortis est.
3. Item cognoscit quod voluntarie agitur in praemissis nec contradicentes volunt condescendere juri et meliori dictae ecclesiae et fabricae, sed volunt aut per eorum lucrum aut timorem, quia voluerunt consequi fabricam super defectibus, aut obstinatione vincere causam, et pro tanto petit dictus magister Johannes committi debere IV vel VI vel XII ex melioribus inzigneriis expertis in talibus, sive de Alamania, sive de Anglia, sive de Franzia, cum aliter dicta fabrica ruet pro certo, quod erit magnum damnum universimodo. Ulterius pro veritate evidenti et sui honoris conservatione accedere vult ad presentiam illustrissimi domini Domini et eidem praedicta et alia latius explicare. Item significat quod pro bono ecclesiae foret bonum alibi laborare in dicta ecclesia quam super locis defectuosis saltem usquequo fuerit clare provisum et decisum super istis defectibus.
Item dicunt et respondent [the Lombard masters] in eodem capitulo quod ubi dicit [sic: ‘dicitur’] quod scientia geometrica non debet in iis locum habere, dicunt suprascripti quod si hoc testante videlicet per regulam geometriae Aristotulus dixit hominis autem motus secundum locum quem vocamus lationem, aut reclusus aut circularis aut ex eis mixtus. Item idem dixit [Aristotle] alibi omne corpus perfectum est in tribus et motus ipsius et dictae ecclesiae ascendit ad triangulum ut jam declaratum fuit per alios inzignerios, unde dicunt quod omnia sunt per rectam lineam, aut per sextum: ergo concluditur quod quae facta sunt, sunt facta per geometriam et per praticam, quia ipse dixit [Aristotle] quod scientia sine arte nihil est; de arte autem jam responsum est in aliis capitulis.
Doc. III: 1401, 15 May
(AFDMi, Ordinazioni capitolari, I, cc. 264v –270v; Nava, Memorie e documenti, pp. 107–15; Annali, I, pp. 224–29. Translation by ‘Annali’)
The architects discussing Mignot's project (a return to Stornaloco I) agree instead to the continuation of Stornaloco II, with the exception of the Frenchman Giovanni Alcherio and the Deputati Guidolo Della Croce and Simone da Cavagnera, who had supervised the construction of the model illustrating Stornaloco I in 1391–92, and had fierce objections to proceeding with Stornaloco II (c. 264v: ‘qui vero non erant contenti, surgerent et surrexerunt et dicte infrascripte deliberationi non conscensserunt’). The Annali presents an Italian translation of the Latin original.
Si interroghino gli ingegneri infranominati, e tutte le persone infrascritte intorno ai capitoli sotto notati, ai quali daranno le loro risposte per iscritto.
Maestro Giovanni Mignoto di Francia, maestro Marco da Carona, maestro Antonino da Paderno, maestro Giovanni da Giussano dei frati predicatori, maestro Andriolo de’ Ferrari dei frati minori, Simone de’ Cavagnera, Giovanni Scrosato fabbro, Giovanni Alcherio, Onofrio de’ Serina, Lorenzo Donato, Ambrogio Manizia, Gabriele de’ Rho, Galleto de’ Belloni fabbro, Guidolo della Croce, Porolo da Calco.
[…]
VII Domanda: Se seguendo la forma del secondo progetto [Mignot and Stornaloco I] si muterebbero soltanto per questa opera le precedenti disposizioni [Stornaloco II] circa la maggiore altezza o larghezza della chiesa, o in qualche sua forma sostanziale?
Carona: La risposta è che si varierebbe l'ordine stabilito dagli altri ingegneri, secondo il già principiato [Stornaloco II].
Paderno: Rispondo che siccome il disegno presentato da maestro Giovanni [Mignot] non contiene alcuna dimostrazione circa all'altezza di tutti gli archi, come era stato fatto dagli altri ingegneri, così non posso rispondere intorno all'altezza della crociera se non che esso non ne fece cenno nel suo disegno.
Serina: Risponde che la navata principale di mezzo andrebbe ad essere di 8 braccia più alta di quello che era stato disposto prima [Stornaloco II], giusta il disegno e la misura datine da maestro Giovanni [Mignot following Stornaloco I], per cui deve far meraviglia se altre volte lo stesso maestro Giovanni disse che non era solido tutto l'edificio, che ora essendo ancora più alto dovrebbe essere meno solido.
Calco: Risponde che seguendo la forma del nuovo progetto non si varierebbe la disposizione già data relativamente alla maggiore altezza e larghezza, o relativamente a qualche forma sostanziale, ma solamente quanto alla maggior grossezza del corpo dell'edificio.
Donato: In confronto di quella prima ordinata [Stornaloco II] si fa qualche variazione all'altezza compiendo il progetto Mignoto [Stornaloco I], ma questa variazione è lodevole perché segue la ragione geometrica del triangolo.Footnote 1
Alcherio: Se non erro, col progetto Mignoto [Stornaloco I] si fa qualche variazione nell'altezza, ma qualunque variazione succeda per lo stesso, sarà un miglioramento della solidità, della congruità, della bellezza, e della celerità di costruzione della fabbrica, e ciò riescirà un gravissimo documento [sic: ‘nocumentum’] contro i ciechi che fingono di essere geometri.Footnote 2
Della Croce: Seguendo la forma del secondo progetto [Stornaloco I and Mignot] si muta il falso ordine già disposto [Stornaloco II], e si rispetta il retto ordine del triangolo, che non può essere abbandonato senza errore, come altre volte maestro Enrico, e certo maestro Annex tedesco, prima di lui, predicarono con alta e fedele voce nelle orecchie dei falsi sordi.
Scrosato: Rispondo che se si varia qualche disposizione precedente [Stornaloco II], la si varia in meglio, in più bello e più lodevole modo, secondo la geometria triangolare.Footnote 3
Galleto: Dico che seguendo il nuovo progetto si muterebbe la disposizione precedente [going back to Stornaloco I from Stornaloco II], ma questo non si allontana dalla forma triangolare, dalla quale nessun geometra perito non può né deve recedere, cosicché anche con qualche variazione non si abbandona la suddetta forma triangolare, ciò che vidi fatto anche da altri maestri periti in simili cose.
Cavagnera: Dicho che otegniando lo modo di magistro Johanne, zoè per li archi e croxere tanto che la nostra gexia non andava ni più bassa ni più alta, né si difformava a nessuna provvisione data in fata.