Article contents
SELECTIVE WITHDRAWAL OF A TWO-LAYER VISCOUS FLUID
Published online by Cambridge University Press: 08 February 2013
Abstract
Selective withdrawal of a two-layer fluid is considered. The fluid layers are weakly compressible, miscible and viscous and therefore flow rotationally. The lower, denser fluid flows with constant velocity out through one or more drain holes in the bottom of a rectangular tank. The drain is opened impulsively and the subsequent draw-down produces waves in the interface which travel outward to the edges of the tank and are reflected back with a 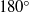 $18{0}^{\circ } $ change of phase. The points on the interface that have the highest absolute gradient form regions of high vorticity in the tank, enabling mixing of the fluids. An inviscid linearized interface is computed and compared to contour plots of density for the viscous solution. The two agree closely at early times in the withdrawal process, but as time increases, nonlinear and viscous effects take over. The time at which the lighter fluid starts to flow out of the tank is dependent on the number of drains, their width, and the fluid flow rate and density, and is investigated here.
$18{0}^{\circ } $ change of phase. The points on the interface that have the highest absolute gradient form regions of high vorticity in the tank, enabling mixing of the fluids. An inviscid linearized interface is computed and compared to contour plots of density for the viscous solution. The two agree closely at early times in the withdrawal process, but as time increases, nonlinear and viscous effects take over. The time at which the lighter fluid starts to flow out of the tank is dependent on the number of drains, their width, and the fluid flow rate and density, and is investigated here.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright ©2013 Australian Mathematical Society
References
- 2
- Cited by


