Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-20T02:57:52.627Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE 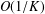$O(1/K)$ CONVERGENCE RATE OF THE ALTERNATING DIRECTION METHOD OF MULTIPLIERS IN A COMPLEX DOMAIN

Part of: Control systems

Published online by Cambridge University Press:  30 August 2018

L. LI Open the ORCID record for L. LI [Opens in a new window] ,
G. Q. WANG  and
J. L. ZHANG
L. LI*
Affiliation:
School of Mathematics, Physics and Statistics, Shanghai University of Engineering Science, Shanghai, China email lilu@sues.edu.cn, guoq_wang@hotmail.com, xzhzhangjuli@163.com
G. Q. WANG
Affiliation:
School of Mathematics, Physics and Statistics, Shanghai University of Engineering Science, Shanghai, China email lilu@sues.edu.cn, guoq_wang@hotmail.com, xzhzhangjuli@163.com
J. L. ZHANG
Affiliation:
School of Mathematics, Physics and Statistics, Shanghai University of Engineering Science, Shanghai, China email lilu@sues.edu.cn, guoq_wang@hotmail.com, xzhzhangjuli@163.com
*
✉lilu@sues.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We focus on the convergence rate of the alternating direction method of multipliers (ADMM) in a complex domain. First, the complex form of variational inequality (VI) is established by using the Wirtinger calculus technique. Second, the 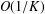$O(1/K)$ convergence rate of the ADMM in a complex domain is provided. Third, the ADMM in a complex domain is applied to the least absolute shrinkage and selectionator operator (LASSO). Finally, numerical simulations are provided to show that ADMM in a complex domain has the 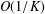$O(1/K)$ convergence rate and that it has certain advantages compared with the ADMM in a real domain.

Keywords

the alternating direction method of multipliersconvergence rateWirtinger calculusleast absolute shrinkage and selectionator operator

MSC classification

Primary: 90C25: Convex programming
Secondary: 65K10: Optimization and variational techniques 93C83: Control problems involving computers (process control, etc.)
Type
Research Article
Information
The ANZIAM Journal , Volume 60 , Issue 1 , July 2018 , pp. 95 - 117
Copyright
© 2018 Australian Mathematical Society 

References

Bai, Y. Q. and Shen, K. J., “Alternating direction method of multipliers for $\ell _{1}{-}\ell _{2}$ -regularized logistic regression model”, J. Oper. Res. Soc. China 4 (2016) 243–253; doi:10.1007/s40305-015-0090-2.Google Scholar
Boyd, S., Parikh, N., Chu, E., Peleato, B. and Eckstein, J., “Distributed optimization and statistical learning via the alternating direction method of multipliers”, Found. Trends Mach. Learn. 3 (2011) 1–122; doi:10.1561/2200000016.Google Scholar
Cai, X. J., Han, D. R. and Yuan, X. M., “On the convergence of the direct extension of ADMM for three-block separable convex minimization models with one strongly convex function”, Comput. Optim. Appl. 66 (2017) 39–73; doi:10.1007/s10589-016-9860-y.Google Scholar
Candès, E. J., Romberg, J. and Tao, T., “Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information”, IEEE Trans. Inform. Theory 52 (2006) 489–509; doi:10.1109/TIT.2005.862083.Google Scholar
Cottle, R. W., Giannessi, F. and Lions, J. L., Variational inequalities and complementarity problems: theory and applications (Wiley, Chichester, 1980); doi:10.1002/zamm.19810610316.Google Scholar
Dafermosa, S. C., “An iterative scheme for variational inequalities”, Math. Program. 26 (1983) 40–47; doi:10.1007/BF02591891.Google Scholar
Donoho, D. L., “Compressed sensing”, IEEE Trans. Inform. Theory 52 (2006) 1289–1306; doi:10.1109/TIT.2006.871582.Google Scholar
Eckstein, J. and Bertsekas, D. P., “On the Douglas–Rachford splitting method and the proximal point algorithm for maximal monotone operators”, Math. Program. 55 (1992) 293–318; doi:10.1007/BF01581204.Google Scholar
Fichera, G., “Abstract unilateral problems”, in: Conference on the theory of ordinary and partial differential equations (2006) 51–64; doi:10.1007/BFb0066918.Google Scholar
Gabay, D., “Applications of the method of multipliers to variational inequalities”, Stud. Math. Appl. 15 (1983) 299–331; doi:10.1016/S0168-2024(08)70034-1.Google Scholar
Gabay, D. and Mercier, B., “A dual algorithm for the solution of nonlinear variational problems via finite element approximation”, Comput. Math. Appl. 2 (1976) 17–40; doi:10.1016/0898-1221(76)90003-1.Google Scholar
Glowinski, R., Lions, J. L. and Tremoliérès, R., Numerical analysis of variational inequalities (North-Holland, Amsterdam, 1981); ISBN: 9780080875293.Google Scholar
Grant, M. and Boyd, S., “CVX: Matlab software for disciplined convex programming, version 2.1”, (2014); http://cvxr.com/cvx.Google Scholar
Hastie, T., Tibshirani, R. and Friedman, J., The elements of statistical learning: data mining, inference and prediction (Springer, New York, 2009); doi:10.1007/978-0-387-84858-7.Google Scholar
He, B. S. and Yuan, X. M., “On the $O(1/n)$ convergence rate of the Douglas–Rachford alternating direction method”, SIAM J. Numer. Anal. 50 (2012) 700–709; doi:10.1137/110836936.Google Scholar
He, B. S. and Yuan, X. M., “On non-ergodic convergence rate of Douglas–Rachford alternating direction method of multipliers”, Numer. Math. 130 (2015) 567–577; doi:10.1007/s00211-014-0673-6.Google Scholar
Hestenes, M. R., “Multiplier and gradient methods”, J. Optim. Theory Appl. 4 (1969) 303–320; doi:10.1007/BF00927673.Google Scholar
Hinamoto, T., Doi, A. and Lu, W. S., “Realization of 3-D separable-denominator digital filters with low $l_{2}$ -sensitivity”, IEEE Trans. Signal Process. 60 (2012) 6282–6293; doi:10.1109/TSP.2012.2215027.Google Scholar
Li, C. J., Liu, C., Deng, K., Yu, X. H. and Huang, T. W., “Data-driven charging strategy of PEVs under transformer aging risk”, IEEE Trans. Control Syst. Technol. Vol PP (2017) 1–14; doi:10.1109/TCST.2017.2713321.Google Scholar
Li, J. Y., Li, C. J., Wu, Z. Y., Wang, X. Y., Teo, K. L. and Wu, C. Z., “Sparsity-promoting distributed charging control for plug-in electric vehicles over distribution networks”, Appl. Math. Model. 58 (2018) 111–127; doi:10.1016/j.apm.2017.10.034.Google Scholar
Li, J. Y., Li, C. J., Xu, Y., Dong, Z., Wong, K. and Huang, T. W., “Noncooperative game-based distributed charging control for plug-in electric vehicles in distribution networks”, IEEE Trans. Ind. Inform. 14 (2018) 301–310; doi:10.1109/TII.2016.2632761.Google Scholar
Li, L., Wang, X. Y. and Wang, G. Q., “Alternating direction method of multipliers for separable convex optimization of real functions in complex variables”, Math. Probl. Eng. 2015 (2015) 1–14; doi:10.1155/2015/104531.Google Scholar
Lin, T. Y., Ma, S. Q. and Zhang, S. Z., “On the sublinear convergence rate of multi-block ADMM”, J. Oper. Res. Soc. China 3 (2015) 251–274; doi:10.1007/s40305-015-0092-0.Google Scholar
Lofberg, J., “YALMIP: a toolbox for modeling and optimization in MATLAB”, Optim. 2004 (2004) 284–289; doi:10.1109/CACSD.2004.1393890.Google Scholar
Lu, W. S. and Hinamoto, T., “Two-dimensional digital filters with sparse coefficients”, Multidimens. Syst. Signal Process. 22 (2011) 173–189; doi:10.1007/s11045-010-0129-9.Google Scholar
Monteiro, R. D. C. and Svaiter, B. F., “Iteration-complexity of block-decomposition algorithms and the alternating direction method of multipliers”, SIAM J. Optim. 23 (2010) 475–507; doi:10.1137/110849468.Google Scholar
Ng, M., Weiss, P. and Yuan, X. M., “Solving constrained total-variation image restoration and reconstruction problems via alternating direction methods”, SIAM J. Sci. Comput. 32 (2010) 2710–2736; doi:10.1137/090774823.Google Scholar
Rudin, L. I., Osher, S. and Fatemi, E., “Nonlinear total variation based noise removal algorithms”, in: Experimental mathematics, computational issues in nonlinear science: Proc. of the Eleventh Annual Int. Conf. of the Center for Nonlinear Studies, Los Alamos, NM, USA, 20–24 May 1991. Volume 60 (Elsevier Science Publishers B.V., Amsterdam, 1992) 259–268; doi:10.1016/0167-2789(92)90242-F.Google Scholar
Scheinberg, K., Ma, S. Q. and Goldfarb, D., “Sparse inverse covariance selection via alternating linearization methods”, in: Twenty-fourth annual conference on neural information processing systems (NIPS) Vancouver, Canada, 6–9 December, 2010, Volume 23 Advances in Neural Information Processing Systems (Curran Associates Inc., Red Hook, New York, 2010) 2101–2109; ISBN: 978-1-61782-380-0.Google Scholar
Sorber, L., Barel, M. V. and Lathauwer, L. D., “Unconstrained optimization of real functions in complex variables”, SIAM J. Optim. 22 (2012) 8791–8898; doi:10.1137/110832124.Google Scholar
Sturm, J. F., “Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cons”, Optim. Methods Softw. 11 (1999) 625–653; doi:10.1080/10556789908805766.Google Scholar
Tibshirani, R., “Regression shrinkage selection via the LASSO”, J. R. Stat. Soc. Ser. B Stat. Methodol. 58 (1996) 267–288; URL: http://www.jstor.org/stable/2346178.Google Scholar
Toh, K. C., Todd, M. J. and Tütüncü, R. H., “SDPT3 – a Matlab software package for semidefinite programming, Version 1.3”, Optim. Methods Softw. 11 (1999) 545–581; doi:10.1080/10556789908805762.Google Scholar
Zhao, L. and Dafermos, S., “General economic equilibrium and variational inequalities”, Oper. Res. Lett. 10 (1991) 369–376; doi:10.1016/0167-6377(91)90037-P.Google Scholar