No CrossRef data available.
Article contents
AN OPTIMAL LINEAR FILTER FOR ESTIMATION OF RANDOM FUNCTIONS IN HILBERT SPACE
Published online by Cambridge University Press: 07 January 2021
Abstract
Let 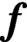 $\boldsymbol{f}$
be a square-integrable, zero-mean, random vector with observable realizations in a Hilbert space H, and let
$\boldsymbol{f}$
be a square-integrable, zero-mean, random vector with observable realizations in a Hilbert space H, and let 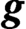 $\boldsymbol{g}$
be an associated square-integrable, zero-mean, random vector with realizations which are not observable in a Hilbert space K. We seek an optimal filter in the form of a closed linear operator X acting on the observable realizations of a proximate vector
$\boldsymbol{g}$
be an associated square-integrable, zero-mean, random vector with realizations which are not observable in a Hilbert space K. We seek an optimal filter in the form of a closed linear operator X acting on the observable realizations of a proximate vector 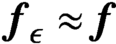 $\boldsymbol{f}_{\epsilon } \approx \boldsymbol{f}$
that provides the best estimate
$\boldsymbol{f}_{\epsilon } \approx \boldsymbol{f}$
that provides the best estimate 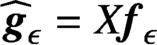 $\widehat{\boldsymbol{g}}_{\epsilon} = X \boldsymbol{f}_{\epsilon}$
of the vector
$\widehat{\boldsymbol{g}}_{\epsilon} = X \boldsymbol{f}_{\epsilon}$
of the vector 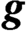 $\boldsymbol{g}$
. We assume the required covariance operators are known. The results are illustrated with a typical example.
$\boldsymbol{g}$
. We assume the required covariance operators are known. The results are illustrated with a typical example.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © Australian Mathematical Society 2021





