Introduction
Between 1993 and 2003, Greenland contributed 0.21±0.07mma–1 to global mean sea-level rise (Reference Lemke and SolomonLemke and others, 2007). This contribution is projected to increase to 0.3–1.9mma–1 for the period 2090–99 (Reference Meehl and SolomonMeehl and others, 2007). While some of the present and projected contribution is from direct meltwater runoff, most of the contribution is due to changes in ice dynamics, namely faster flow velocities of outlet glaciers, and the resultant increase in the calving of solid ice into the oceans. Enhanced surface meltwater generation can play a role in these flow-speed accelerations via increased subglacial lubrication facilitated by larger amounts of water reaching the bed (Reference Boon and SharpBoon and Sharp, 2003; Reference Parizek and AlleyParizek and Alley, 2004; Reference Van der VeenVan der Veen, 2007; Reference DasDas and others, 2008; Reference Bartholomew, Nienow, Mair, Hubbard, King and SoleBartholomew and others, 2010). Observational evidence supports this process (Reference Zwally, Abdalati, Herring, Larson, Saba and SteffenZwally and others, 2002; Reference Van de WalVan de Wal and others, 2008; Reference Shepherd, Hubbard, Nienow, McMillan and JoughinShepherd and others, 2009) although its effect on outlet glacier speeds is unclear (Reference Joughin, Das, King, Smith, Howat and MoonJoughin and others, 2008). Our understanding of this complex process is limited, in part, by our knowledge of the minimum quantity of meltwater needed, and the timing of its availability, to initiate and sustain increased glacier flow rates (Reference Parizek and AlleyParizek and Alley, 2004).
We previously developed a method for determining the depth and, hence, the volume of surface melt ponds by applying a radiative transfer model to multispectral Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) imagery (Reference Sneed and HamiltonSneed and Hamilton, 2007). In principle, the algorithm can also be applied to other types of visible imagery, such as Landsat 7 Enhanced Thematic Mapper Plus (ETM+), and Moderate Resolution Imaging Spectroradiometer (MODIS) satellite sensor images. The bands of interest are: VNIR1 (520–600 nm) and VNIR3N (780–860 nm) for ASTER; band 2 (525–605 nm) and band 4 (750–900 nm) for Landsat 7; and band 4 (545–565 nm) and band 2 (841–876 nm) for MODIS. The method used for extracting water depth and bottom albedo is based on Bouguer–Lambert–Beer’s law
where I(z,λ) is the water-leaving spectral intensity at some depth, I(0,λ) is the spectral intensity at zero depth, Kλ is the spectral attenuation and z is depth. Written in terms of reflectance and inverted to logarithmic form (Reference PhilpotPhilpot, 1989),
where g is given below, A d is the bottom or substrate albedo (reflectance), R ∞ is the reflectance for optically deep water and Rw is the reflectance of some pixel of interest. As a practical matter, R ∞ is reflectance from optically deep water where the influence of bottom reflectance is nil; it can be derived from water that is deeper than ~40 m. With values for R ∞, g and Rw in hand, A d must be determined before the water depth, z, of the pixel of interest can be calculated. Details of the procedure for determining A d are given by Reference Sneed and HamiltonSneed and Hamilton (2007, section 2.3). The quantity g is
where K d is the diffuse attenuation coefficient for downwelling light, a is the beam absorption coefficient and D u an upwelling light distribution function or the reciprocal of the upwelling average cosine (Reference MobleyMobley, 1994).
The depth retrieval algorithm contains several simplifying assumptions:
Suspended or dissolved, organic or inorganic, particulate matter is minimal.
There is no wind, and therefore there are no waves, on a pond’s surface.
There is no inelastic scattering (e.g. Raman scattering or fluorescence).
The substrate of a melt pond is homogeneous and parallel to the surface.
An additional unstated assumption of Reference Sneed and HamiltonSneed and Hamilton (2007) is that the image containing surface meltwater and melt ponds must also contain optically deep water suitable for deriving R ∞. In practice, this means that suitable images must cover both the ice-sheet margin and adjacent regions of ice-free ocean, a potential limitation for ASTER images which are only 65 km×65km and the 185 km ×185 km Landsat 7 ETM+ images.
Here we examine the validity of the above assumptions based on new theoretical analyses and field observations on an East Greenland melt pond in July 2008.
Helheim Glacier, East Greenland
In situ data
On 11 July 2008 we carried out a depth survey of a melt pond on Helheim Glacier from a rowed, inflatable boat with simultaneous radiometric and global positioning (GPS) measurements. A digital fathometer with a measured accuracy of 0.03m was used to collect water depths, and a Garmin® hand-held GPS provided position coordinates. A Satlantic Profiler II® (Satlantic, Inc., Halifax, Nova Scotia, Canada) with two hyperspectral radiometers (operated in the surface mode) was used to collect above- and below-water radiometric data. The downwelling surface irradiance radiometer with a cosine detector was positioned ~15 cm above the water surface while the upwelling, water-leaving radiance radiometer was positioned ~10 cm below the water surface. The radiometers were towed 5–10m behind the boat and every effort was made to not cast a shadow on the pond bottom below the radiometers. Depth and GPS data were recorded by hand and radiometric data were collected on a laptop computer. The physical configuration of the Profiler II® precluded gathering radiometric data in water shallower than ~0.5 m, although depth and GPS measurements were made in shallow water.
Measurements began at 12:51 local time (UTC-2) and ended at 13:41 local time (UTC-2). There was no detectable wind, the pond surface was calm and the sky was clear except for a few scattered high clouds. Our somewhat meandering course covered a straight-line distance of ~200m on the long axis of the pond and we recorded 21 depths and 3 GPS positions. The shallowest depth, of 0.7 m, was recorded near 66.46231N, 038.45100˚ W (524465.0E, 7371604.0N UTM 24N) and the deepest depth, of 3.0 m, recorded near 66.46145N, 038.44996˚ W (524512.0E, 7371454.0N UTM 24N). It should be noted that our deepest recorded depth was not necessarily the deepest part of the pond. We also observed a number of scattered cryoconite holes in the pond bottom that appeared to be ~5–15cm in diameter. An examination of more than 3600 upwelling radiance, Lw (0–), values at 475 and 555 nm shows occasional sudden and transient decreases which probably indicate cryoconite holes.
Satellite-derived data
A satellite image from the Advanced Land Observing Satellite (ALOS, 10m spatial resolution) for 22 June 2008 shows a roughly elliptical pond with a major axis of ~1200m oriented in a northwest–southeast direction and a minor axis of ~500 m. An ASTER image of 3 August 2008 (15m spatial resolution) shows the pond reduced to scattered segments; the area where the in situ data of 11 July were collected is completely devoid of water. However, a Landsat 7 (30m spatial resolution) image of 20 July 2008 (pathnrow, 232n013) does contain the pond segment we measured on 11 July (Fig. 1) and was used to calculate water depths, using Equation (2). Another Landsat 7 image of 20 July (path\row, 232\014) provided the R ∞ data.

Fig. 1. A portion of the 20 July 2008 Landsat 7 image showing the melt ponds on Helheim Glacier, East Greenland. The red ellipse indicates the pond where the 11 July 2008 measurements were made.
Both images were subsetted to speed up processing, converted to top-of-atmosphere reflectance (Reference IrishIrish, 1999), and atmospherically corrected using the 6SV radiative-transfer modeling code of Reference Vermote, Tanré, Deuzé, Herman, Morcrette and KotchenovaVermote and others (2005). Water depths were calculated following the procedures set out by Reference Sneed and HamiltonSneed and Hamilton (2007, section 2.3). The following numerical values were used to calculate the water depths shown in Figure 2: A d, 0.5639; R ∞, 0.0380; g, 0.1180 m–1; solar zenith, 47.0387˚; and an index of refraction for sea water of 1.33157. Because of the large spatial resolution of the Landsat image, it is not possible to attribute a measured depth at a particular location to a particular pixel in Figure 2. However, the depth map does show decreasing depths at the northwest and southeast ends of the pond and a deep area near the middle, all of which are consistent with the depths we measured at those locations.
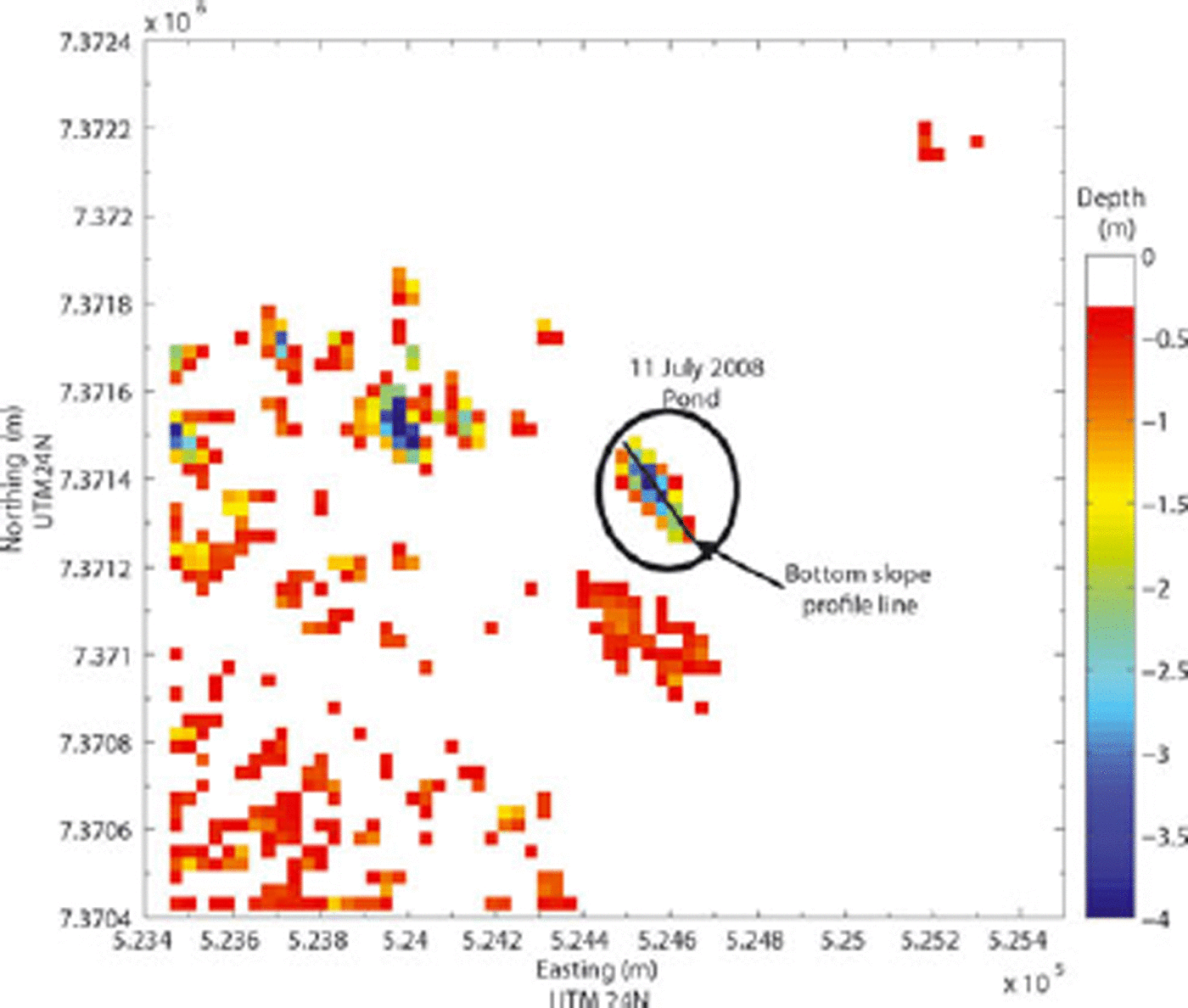
Fig. 2. A water-depth map of the melt pond where the 11 July measurements were made.
Assumptions
Suspended and dissolved matter
Meltwater samples were recovered from a melt pond on Helheim Glacier in July 2007 and July 2008 for detailed optical and chemical analyses. The melt pond lies ~100km inland from the Atlantic Ocean at an elevation of ~600m and is equidistant (~3 km) from two large nunataks. Not surprisingly, ion chromatography analysis of the water shows a strong marine influence. Methylsulfonate (MS–) is present (2.12 and 0.40 μgL–1 in the 2007 and 2008 samples, respectively), and is an indirect product of marine biota (Reference Legrand and MayewskiLegrand and Mayewski, 1997). The sodium (Na+) and chloride (Cl–) ratios for both years (0.545 and 0.515) are close to the sea-water (salinity, S = 35) ratio of 0.557 (Reference PilsonPilson, 1998) and are a further indication of a marine source. The concentrations of the other major ions (K+, Mg2+, Ca2+, NO3 – and SO4 2–) are consistent with the minimum concentrations found in snow throughout the Arctic. The calcium (Ca2+), potassium (K+) and magnesium (Mg2+) are most likely derived from terrestrial dust, while the NO3 – and SO4 2 – are linked to human activities (Reference Legrand and MayewskiLegrand and Mayewski, 1997; De Caritat and others, 2005). The concentrations of K+ and Mg2+ for both years are near the instrumental detection limit and are commensurate with the low levels of particulate scattering measured by the optical analyses below.
For the optical analyses, spectral transmittance and spectral absorption were measured at nine wavelengths using a WETLabs (Philomath, OR, USA) ac-9® absorption and attenuation meter. The spectral absorption coefficient, a, and the spectral beam attenuation coefficient, c, are derived from the ac-9 measurements. The ac-9 samples nine bands but we are primarily interested in the one centered at 555 nm, because it is very near the midpoints of the ASTER, Landsat and MODIS bands used to calculate water depth.
The absorption coefficient, a (particulate and dissolved) is near the instrument’s resolution limits, a = 0.003 and 0.010m–1 at 555 nm for 2007 and 2008, respectively. Particulate scattering, b, is not measured directly but derived from the energy equation, c = a + b. The scattering coefficients are b = 0.050 and 0.014m–1 at 555 nm, in 2007 and 2008, respectively. By way of comparison, Reference Smith and BakerSmith and Baker (1981) analyzed fresh water from Crater Lake, Oregon, USA, and reported a = 0.0638m–1 and b = 0.0015 m–1 at 550 nm while Reference Davies-ColleyDavies-Colley (1983) reported on three shallow lakes in New Zealand with absorption coefficients, a, of ~0.5–~1.4m–1 and scattering coefficients, b, of 3.2–30m–1 at 550 nm.
The slopes of the spectral scattering curves for both years are very similar, as are the slopes of the concomitant particle-size distribution curves (Reference Boss, Twardowski and HerringBoss and others, 2001), indicating that the bulk of the particulate matter has a distribution similar to that of small particles (Reference Babin, Morel, Fournier-Sicre, Fell and StramskiBabin and others, 2003). Reference Babin, Morel, Fournier-Sicre, Fell and StramskiBabin and others (2003) showed the close relationship between an increasing backscattering coefficient, b b(λ), and an increase of suspended particulate matter measured by dry weight per unit volume of sea water (gm–3). A similar relation should hold for backscatter coefficient and particle load in a freshwater melt pond, so any bias introduced by particulates in the calculated water depth will be minimal, given the small measured values of a and b in our samples.
Wind and waves
Quantifying the effects of wind and the resultant waves on the water depth calculated using Equation (2) requires that we know the wind speed in the area of the melt pond. The large size (>1 km in diameter) of some ponds introduces the possibility that light could be specularly reflected from a wave facet to the satellite sensor, producing sun glint given the required confluence of solar and sensor relative azimuth, wind speed, wind direction and wave-facet slope. This is an unlikely scenario for most of the ice sheet, so instead we take a modeling approach. Consider a circular pond with a diameter of 1 km and an idealized uniform depth of 15 m. It is possible to calculate wave amplitudes for a given wind speed, water depth and fetch from first principles (e.g. http://woodshole.er.usgs.gov/staffpages/csherwood/sedx_equations/RunSPMWave.html; Table 1).
Table 1. Shallow water wave amplitude as a function of wind speed, fetch and water depth
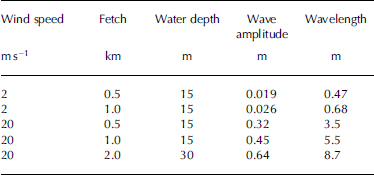
Reference Zaneveld, Boss and HwangZaneveld and others (2001) modeled remote-sensing reflectance, R rs, as a function of wave amplitude and the angle between the light source and the sensor at a small fixed wavelength, 0.01 m. A conservative value for this angle using an ASTER image is 5. Given the first four wave amplitudes in Table 1 and a look angle of 5, R rs would increase by ~5% with a 20 ms–1 wind, and, with the last set of values, R rs might increase by 10–11% (Reference Zaneveld, Boss and HwangZaneveld and others, 2001, fig. 3). As the period and wavelength increase beyond the small value used by Reference Zaneveld, Boss and HwangZaneveld and others (2001) we expect the wave effect on remote-sensing reflectance (and other apparent optical properties) to diminish due to spatial averaging. To test the sensitivity of remote-sensing reflectance to surface wind speed, five modeling runs were performed using HYDROLIGHT®. We varied the wind speed between 0 and 14.9ms–1, the maximum allowed by the software, while holding all other input parameters fixed, and observed only a 1.4% decrease in the remote-sensing reflectance. Thus, we conclude that the effect of waves on the optical signal at the satellite, and derived water depths, is relatively unimportant.

Fig. 3. A portion of an ASTER image (5 August 2009) of the Nioghalvfjerdsfjorden glacier ice tongue, northeast Greenland, near the terminus. Red ellipses outline areas of cryoconite. This area was photographed from a helicopter by one of us (G.S.H.) in early September 2009, and a sample of cryoconite was retrieved.
Inelastic scattering
There is always inelastic scattering of light by natural waters (salt or fresh) at visible wavelengths. Molecular or Raman scattering is always present and fluorescence, due to dissolved or suspended organic material, can also occur. As particulate matter (organic or inorganic) decreases, the effects of elastic scattering on the in-water and above-water light fields diminishes and scattering is mainly by inelastic collisions. As fluorescence decreases, the contribution of Raman scattering to the light field becomes more pronounced (e.g. Morel and Gentili, 1991; Morel and Loisel, 1998). But, as Reference GordonGordon (1999) points out, Raman scattering in natural waters is relevant to the remote sensing of ocean color and its use as a proxy for oceanic biological productivity. Here our interest is much simpler – to determine the depth of a glacial melt pond – and it is not necessary to partition the bulk scattering coefficient between elastic and inelastic collisions.
Substrate homogeneity and bottom slope
We originally assumed that the bottom of a melt pond or meltwater channel was ice with the same albedo throughout. However, we observed numerous cryoconite holes (~5–15cm in diameter) in the bottom of the Helheim Glacier melt pond. These holes raise the possibility that larger areas of cryoconite might collect in the deepest parts of a pond or at the bends of a meltwater channel where water velocity slows. Detecting such areas and quantifying their effect on calculated water depth is not trivial, although the latter is the easier of the two problems.
Reference GadjaGadja (1958) described cryoconite as a fine, or very fine, dark, wind-blown dust composed of organic and/or inorganic material deposited on snow or ice surfaces, and Reference Gerdel and DrouetGerdel and Drouet (1960) described the color as dark brown to blue/black. Reference TakeuchiTakeuchi (2002a) analyzed cryoconite from nine glaciers, three in the Himalaya, three in Tibet, one on Baffin Island, one on Axel Heiberg and one on Spitsbergen, for organic and mineral content and spectral reflectance. Takeuchi and colleagues have also measured the spectral reflectance (albedo) of cryoconite in such diverse regions as Patagonia (Reference Takeuchi, Kohshima, Shiraiwa and KubotaTakeuchi and others, 2001), China (Reference Takeuchi and LiTakeuchi and Li, 2008) and Alaska (Reference TakeuchiTakeuchi, 2002b; Reference Takeuchi, Kohshima and SegawaTakeuchi and others, 2003). Reference Bøggild, Brandt, Brown and WarrenBøggild and others (2010) have measured the spectral albedo of surface cryoconite in northeast Greenland and their values agree well with those of Takeuchi. Thus, if we can detect cryoconite in satellite images, we can correct for its effects on the water-depth calculations. Areas of cryoconite are occasionally large enough to be detected in satellite images, as can be seen in Figure 3, an ASTER image with 15 m spatial resolution. In the case of Figure 3 it is a simple matter to mask out the cryoconite pixels before calculating the water depth and volume in this sub-image.
For pixels that might contain a mixture of cryoconite and water, spectral mixture analysis (SMA) can determine the fractions of each in a pixel (Reference AdamsAdams and others, 1995; Reference Tompkins, Mustard, Pieters and ForsythTompkins and others, 1997). The method of Reference Tompkins, Mustard, Pieters and ForsythTompkins and others (1997) is especially useful because it requires no prior knowledge of the spectra of the components that might mix in a pixel. Nevertheless, the spectral analyses of Takeuchi and colleagues can provide good initial values for determining the end members. The use of SMA in conjunction with the depth algorithm of Reference Sneed and HamiltonSneed and Hamilton (2007) is the next step in the ongoing refinement of the algorithm.
We have also assumed the slope of the bottom for any given pixel is very small, i.e. that a bottom pixel is more or less parallel to the water surface. When there is a significant slope, the value of A d, the bottom or substrate albedo (reflectance), can be overestimated by as much as 30% (Reference Zaneveld and BossZaneveld and Boss, 2003). A ~400m transect was struck across the melt ponds shown in Figure 2 which contained 12 data points, (Fig. 4). The points were evenly spaced along the transect, with the distance between any two points ~33 m, the approximate size of an ETM+ pixel. The bottom slope angles between adjacent data points were calculated. Figure 5 shows that for this transect the maximum slope angle between any two adjacent points is ~3.5. Reference Mobley and SundmanMobley and Sundman (2003) show that for slopes of 20˚ or less the upwelling radiance error is <10%. At angles of ~1˚ the percentage of error is almost zero (Reference Mobley and SundmanMobley and Sundman, 2003, fig. 6). Our experience has shown that the bottom profile of most melt ponds closely resembles that of Figure 4, so any errors in A d due to bottom slope angles will be very small.

Fig. 4. Bottom profile of the 400m transect.
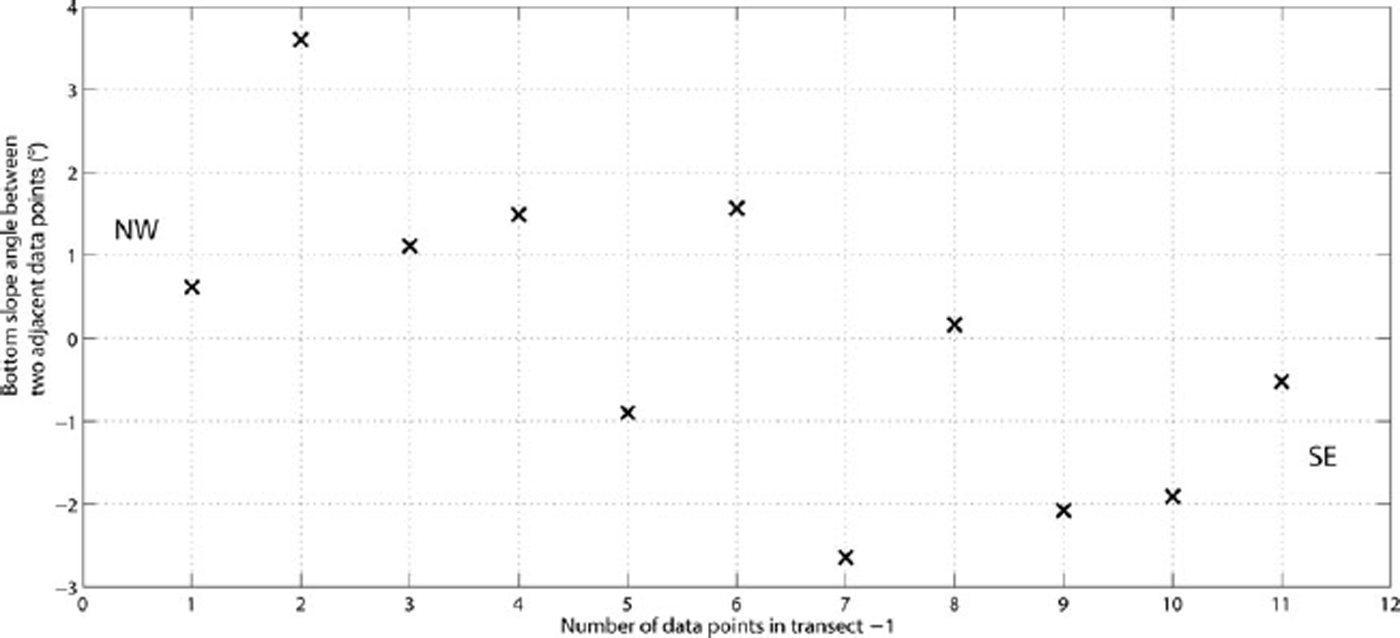
Fig. 5. Bottom slope angles. The angles are between adjacent data points of the 400m melt pond transect.
Dark and deep water
Reflectance over optically deep water where the influence of bottom reflectance is nil, R ∞, can be derived from water that is deeper than ~40m and is one of the two end points needed to solve Equation (2), the other being A d. Ideally, such water would be as similar to the melt pond water as possible, i.e. fresh water with low particle concentrations, and sufficiently deep that the bottom reflectance is nil. Absent such a water body, can we use deep ocean water as a source for R ∞ and what adjustments (if any) must be made in Equation (3) to account for the differing water types?
Temperature, salinity and the beam absorption and scattering coefficients
Reference Pegau and ZaneveldPegau and Zaneveld (1993, fig. 3) show that for six temperatures between 5 and 30˚C, the absorption spectra of fresh and salt water from 550 to 740 nm are virtually identical and Reference SullivanSullivan and others (2006) report no significant temperature dependence between 440 and 550 nm.
For both fresh water and filtered sea water (salinity of ~25 psu) and temperatures varying from 6 to 30˚C, Reference Trabjerg and HøyerslevTrabjerg and Høyerslev (1996) report the absorption coefficient temperature dependence to be –0.00091 ± 0.00006m–1 K–1 in the 400–550nm range, while Reference Pegau, Gray and ZaneveldPegau and others (1997) report a temperature dependence of <0.001m–1 in the range 400–700nm for pure and salt water and temperatures between 15 and 30˚C. Reference Pegau, Gray and ZaneveldPegau and others (1997) suggest that the linear relationship between temperature and the absorption coefficient holds down to the lower temperatures found in the polar seas. It is reasonable to conclude that any temperature differences between a melt pond and a water body that is the source of R ∞ will have a negligible effect on the absorption coefficient in the visible spectrum.
As is the case with temperature, Reference Pegau, Gray and ZaneveldPegau and others (1997) find a very small salinity dependence for the absorption coefficient in the visible spectrum (<0.00015m–1 (psu)–1) the exception being, as with temperature, in the near-infrared. Reference Pope and FryPope and Fry (1997) report absorption coefficients of 0.00635 and 0.0565 m–1 for 440 and 550 nm, respectively. At 555 nm, a difference of 30 psu might reduce the absorption coefficient by 0.0009 m–1 (Reference Pegau, Gray and ZaneveldPegau and others, 1997, table 4). Using Pope and Fry’s absorption data for pure water, Reference SullivanSullivan and others (2006) conclude that pure sea water with a salinity of 36 psu would increase the absorption coefficient by ≤0.002m–1 over the spectral range 400–680 nm. We conclude that salinity differences between a melt pond and ocean water will have a negligible effect on the absorption coefficient in the visible spectrum (Reference MobleyMobley, 1994, ch. 3).
Both temperature and salinity affect the beam scattering coefficient, b, in the visible part of the spectrum (Reference MobleyMobley, 1994; Reference Zhang, Hu and HeZhang and others, 2009). The scattering coefficient of pure sea water is ~30% greater than that of pure water (e.g. at 550 nm b is 0.00145 and 0.00195 m–1 for pure water and pure sea water, respectively; Reference MobleyMobley, 1994, table 3.8). However, the effects of temperature on both pure water and pure sea water are an order of magnitude smaller than those of salinity (Reference MobleyMobley, 1994, table 3.9). In optical remote sensing, the spectral backscattering coefficient, b b(λ), of incident light is of primary interest (see Reference MobleyMobley, 1994, ch. 3 for its derivation).
Particulate matter
The absorption coefficient, a, and the backscattering coefficient, b b(λ), are significantly modified by the concentration and type of particulate matter, although, in the clearest natural waters, scattering by water molecules may contribute 50–80% of the backscattering in the blue region (~500 nm) (Reference Stramski, Boss, Bogucki and VossStramski and others, 2004), but the dissolved salts in ocean water contribute little to backscattering (Reference Zhang, Hu and HeZhang and others, 2009). Such ocean water can be found near Easter Island in the southeastern Pacific Ocean (Reference MorelMorel and others, 2007) but may not be suitable for our purposes. Where might we find such clear water in the Arctic region?
Reference SmithSmith (1973) found ‘optically very clear’ water ~180km northwest of Ellesmere Island and Reference Pak, Peterson and ZaneveldPak and others (1977) found water ~50 km north of Ellesmere where ‘the mass concentrations are very small, and typical of extremely clear ocean water’. Both study sites were near the 1000 m depth contour. In 1998 above the Chukchi plateau (~77˚ N; ~173˚W) Reference PegauPegau (2002) recorded beam attenuation measurements to be 25% larger than Reference SmithSmith (1973) and attributed the difference to increased levels of colored dissolved organic material (CDOM) brought into the Arctic Ocean by the large river systems of Eurasia and Canada and concluded that the water was not the clearest natural water. The inherent optical properties of coastal waters are dominated by terrigenous particulates, CDOM and phytoplankton but in deep ocean waters phytoplankton (living or not) dominate. Therefore, it is reasonable to restrict the search for the source water of R ∞ far from shore in deep water, away from river systems, and, in the Arctic, far from the meltwater plumes of tidewater glaciers.
Ocean water
To investigate whether it is necessary that the image containing meltwater also contain deep-water pixels and to test the sensitivity of volume calculations to varying values of R ∞, ten widely scattered (in space and time) ASTER images with deep ocean water were used to extract small, VNIR1 sub-images (~30 × 30 pixels) of only deep water. Two images are from northwestern Greenland, four from northeastern Greenland, one from southeastern Greenland and three from eastern and southeastern Svalbard. One of the northeastern Greenland images is an ascending pass and the southeastern Greenland image has a low gain setting for VNIR1, rather than a normal gain setting. The ten sub-images were corrected to provide top-of-atmosphere reflectance. An atmospherically corrected ASTER scene (13 July 2004) of a melt pond on the Austfonna ice cap, located on Nordaustlandet, Svalbard, was used to calculate the meltwater volume. One of the ten R ∞ sub-images was derived from this 13 July 2004 image, and its R ∞ value was used to calculate the first meltwater volume. The volumes calculated using the other nine R ∞ sub-images are relative to this first volume. The true depth and volume of this pond are unknown. Table 2 shows the results of the volume calculations. The median volume for trials 2–11 is 5.73 × 106 m3, and the median percentage difference is 2.0%. If we exclude outliers, trials 5 and 6, the medians become 5.69 × 106 m3 and 1.2%, respectively. A close examination of the images used in trials 5 and 6 using the thermal infrared bands revealed that high, thin clouds covered both images used for R ∞.
Table 2. Volume changes for different R ∞ images, Austfonna, Nordaustlandet, Svalbard
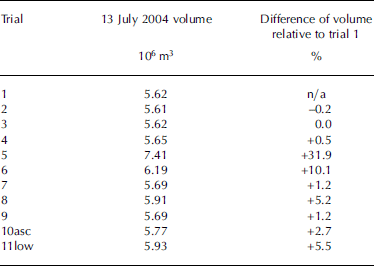
The deep-water sub-images for trials 2, 3, 7 and 9 (those trials with the smallest percentage difference relative to trial 1) are from northeastern Svalbard, southeastern Svalbard, northeastern Greenland and northeastern Greenland, respectively. The image dates for these four trials are 7 July 2004, 4 July 2005, 21 August 2000 and 21 July 2003, respectively.
It is difficult to account for the considerable variation in percentage difference between trials 3 and 8. They are widely separate in space and time: southeastern Svalbard and northeastern Greenland and 4 July 2005 and 10 August 2000, respectively. Trial 8’s sub-image does have the largest off-nadir pointing angle (–8.575˚) of all the trials. However, there are not enough images with varying pointing angles to attempt an analysis of its effect on the calculated volume.
A similar test using Landsat 7 ETM+ images has not been undertaken, nor has one using MODIS images. A variable viewing angle is not an issue with Landsat; however, gain settings can vary depending on surface type and sun elevation angle (Reference IrishIrish, 1999). Given the large number of MODIS data products, the key consideration is to use one that is not a composite of daily orbits, pointing angles and gain settings (e.g. MOD02). As with ASTER images, care should be exercised when choosing ‘blackest’ deep water pixels.
Numerical Modeling
A simple modeling exercise was carried out that compared the deepest depth derived using Equation (2) with that calculated by HYDROLIGHT® (Sequoia Scientific, Inc., Bellevue, WA, USA), a radiative transfer numerical modeling software. In situ, laboratory and satellite data provided the input parameters to HYDROLIGHT®. Additional model inputs of total ozone, column perceptible water vapor and surface pressure data were taken from MODIS, the MOD07 Atmospheric Profile data product for 11 July 2008. The maximum depth calculated by Equation (2) was 4.2 m while the modeled maximum depth (using the Petzold average particle phase function; Reference MobleyMobley, 1994) was 4.1 m, a difference of ~2.4%.
Conclusions
When using the method for determining water depth set out by Reference Sneed and HamiltonSneed and Hamilton (2007) and Equation (2), it is reasonable to assume that inelastic scattering plays no part in that calculation while wind-generated surface waves have a very small effect on the derived depth. Furthermore, we have demonstrated that it is not necessary that the satellite image showing surface meltwater must also contain dark, infinitely deep water. Based on 3 years of water analyses of meltwater from eastern Greenland we are confident that dissolved or suspended particulate matter plays a minor role in accurately determining meltwater depth and volume. Nevertheless, a larger sample set would be welcome and we will continue to collect and analyze meltwater from different regions of Greenland. The assumption of substrate homogeneity remains somewhat problematic and warrants further investigation. Spectral mixture analysis may provide a method for determining what percentage of a pond’s substrate with a different albedo from that of ice would significantly affect the derived depth and volume.
Given the 30m resolution of Landsat 7 ETM+, in situ measured water depths agree reasonably well with those derived from a Landsat image, with the greatest depths found near the center of the pond and the shallowest at the edges. The numerically modeled maximum depth agrees very closely with that from the Landsat image.
Acknowledgements
G.S.H. is supported by NASA’s Cryospheric Sciences Program and W.A.S. is supported by a NASA Earth and Space Science Fellowship. The Dan and Betty Churchill Fund help defray a portion of the fieldwork costs. We thank E. Boss for the loan of radiometers, access to HYDROLIGHT® and discussions, and C. Roesler, W. Slade and M. Estapa for the optical analyses of water samples. We also thank S.B. Sneed for chemical analysis of water samples and J. Saros for the loan of an inflatable research vessel. Finally, thanks to two anonymous reviewers whose comments significantly improved the paper.









