1. Introduction
Snowdrift assessment is a difficult but important challenge. Its effects are various and have implications in many areas such as avalanche-hazard assessment (modification of the snow stability by large-scale redistribution or formation of wind slabs and cornices), snow resource management (ski resorts, water content) or snow defences (roads, buildings). One of the main problems in modelling snowdrift is that one has to work in a full range of scales, from the synoptic to the microtopographical, and one has to consider the permanent interaction between snow, meteorological conditions and local topography. These problems often exceed the present state of the art in different subjects: for example the air turbulent scheme or details of the different snow-transport mechanisms. However, these phenomena cannot be omitted from the framework of automatic snow modelling and avalanche-hazard forecasting.
For about four winter seasons, the Centre d’Études de la Neige (CEN), Météo-France, has run an operational programto determine snow redistributiondue to wind. This program, called SYTRON1 anddescribed in Reference Durand, Guyomarc’h and MérindolDurand and others (2001), is fully integrated into the automatic SAFRAN–Crocus–MÉPRA (SCM) chain (Reference Durand, Giraud, Brun, Mérindol and MartinDurand and others, 1999), and has proven to give reliable results at the massif scale (~500 km2) while showing the need to develop a new and sounder two-dimensional application for smaller scales.
This new software, SYTRON2, is the main subject of this paper. It is a more thorough modelling attempt which runs at a finer horizontal scale (~1kmcharacteristic length divided in a mesh size of 45 m) with a realistic topography at this resolution. It uses some of the SYTRON1 operators, such as the erosion scheme, in order to retain the benefit of the previous validation. The main feature of the new model is its ability to run quickly (in terms of computer time) and to be initialized with the SCM large-scale conditions.
Firstly, we have developed a simple model for the near-surface wind velocity whose output is then modified according to topographic patterns (slope and curvature) at two different resolutions. These resolutions, which exceed the current accuracy of the automatic evaluation of wind and snow in mountainous terrain, must be considered carefully. For simplicity, the calculated (or estimated) wind is kept constant during every hourly time-step and there is no coupling with the snowpack characteristics. Secondly, we have developed some “downscaling operators” to initialize the local snowpack profiles from the SCM massif profiles. A snow profile up to 50 layers is interpolated at each grid-point before being subjected to the wind action.
Once SYTRON2 is initialized with realistic conditions, the model can simulate the occurrence of blowing snow and estimate the total snow mass transport. The losses due to sublimation, as well as the modifications of density and crystal morphology, are considered. The centre of the modelled domain corresponds to our experimental observation site, Col du Lac Blanc, located in the French Alps at about 2700 ma.s.l., where drifting-snow events have been investigated for 10 years (Fig 1a and b).

Fig. 1. Partial views of the test site Col du Lac Blanc, French Alps (2700 m a.s.l.). (a) A southern view of the site showing parts of the instruments and the pole network. The surface state illustrates the important small-scale variability. (b) The snow surface affected by snowdrift, the main transport mode (saltation) and some of the validation poles.
The result is difficult to validate because we lack objective tools to observe all the quantities involved. Tests are performed by using different snow-depth pole measurements (for flux calibration) and photographs of the test site in order to locate erosion and accumulation areas.
2. State of the Art
The snow-modelling efforts of several laboratories have shown the necessity to undertake the numerical study and the modelling of snowdrift phenomena whose effects on avalanche hazards are well known. For many years, field observation campaigns have been conducted and many authors have described and investigated snowdrift (e.g. Reference MellorMellor, 1965; Reference TakeuchiTakeuchi, 1980; Fȯhn and Meister, 1983; Reference Pomeroy and GrayPomeroy and Gray, 1995). More recently, several numerical attempts have been made. Some of them are based on sophisticated models of the different fluxes and the snow–atmosphere interactions (e.g. Reference GauerGauer, 1998a, Reference Gauerb, Reference Gauer2001) and are more suited for a precise treatment of specific wind-transport events. Other realizations are better designed to follow and simulate snowdrift effects in particular locations for a long period (e.g. Reference Liston and SturmListon and Sturm, 1998), but with a limited treatment of the snowpack characteristics.Other attempts are closer to the daily exploitation and can be linked to the daily operational modelling (e.g. Reference Fierz and GauerFierz and Gauer, 1998; Reference Lehning, Doorschot and BarteltLehning and others, 2000a, Reference Lehning, Doorschot, Fierz and Raderschall2002), with the possibility of taking into account the modification of snow crystals.
3. Existing Starting Tools at CEN
3.1. The SCM chain
Our present work is based on the SCM operational chain (Reference Durand, Giraud, Brun, Mérindol and MartinDurand and others, 1999), and aims at improving it for the case of drifting-snow events. The present SCM working scale is about 500 km2 and it is run daily for 23 Alpine and 21 Pyrenean massifs over the whole year. It is used by the professional forecasters in charge of the avalanche-hazard estimation besides other information such as field observations and direct contacts with mountain professionals and users.
The SCM chain simulates the snowpack at different elevations, in vertical steps of 300 m, for different slope aspects of the massifs studied. The results are obtained hourly for three different slope inclinations (flat, 20° and 40°). This is only a rough approximation for the vertical slopes found in real mountain terrain and is one of the main weaknesses of the system, as it cannot take into account small features due to the local effects of wind, topography or vegetation. No explicit parameterization of the snowdrift is incorporated at present, but SCM provides an hourly set of both meteorological and snow conditions, which includes a detailed stratigraphy of all layers. All these quantities are mean values representative of large slopes at different elevations and aspects.
3.2. SYTRON1
Unlike Reference GauerGauer 1998a, Reference Gauerb) or Reference Liston and SturmListon and Sturm (1998), SYTRON1 does not perform a full three-dimensional estimation of the different transport fluxes over a real topography. The model aims only at simulating the effects of a crest between two opposite aspects at all the elevations of SCM considered in steady-state conditions. It is described in detail in Reference Durand, Guyomarc’h and MérindolDurand and others (2001) and Reference Guyomarc’h, Durand, Mérindol and LecorpsGuyomarc’h and others (2002). The basic assumption is a one-dimensional channelled flux forced by the regularly simulated wind. The output is an hourly estimation of the eroded amount on the windward aspect and of the deposited amount on the lee aspect. This model can be considered as an operational application of previous work (e.g. Reference Föhn and MeisterFöhn and Meister, 1983). The computations are done hourly over long periods, without any re-initialization, and are fully embedded in the SCM operational suite which is monitored daily. The evolution of the snow characteristics is determined at once by the snow model Crocus (Reference Brun, Martin, Simon, Gendre and ColéouBrun and others, 1989, Reference Brun, David, Sudul and Brunot1992) and by special operators for the modification of the blowing snow. A flow chart of the operational running mode is shown in Figure 2.

Fig. 2. Flow chart of the links between the different software employed in the final SYTRON2 model.
4. Problem Definition
The goals of this new two-dimensional application are:
To compute an appropriate two-dimensional local wind parameter (such as the shear velocity) in order to assess the initiation and the intensity of the snow transport, through the use of the PROTÉON (Prévision de l’Occurrence de Transport Éolien de la Neige) method presented by Reference Guyomarc’h and MérindolGuyomarc’h and Mérindol (1998), and in order to force the wind advection scheme for the suspended snow at each time-step.
To define the occurrence of blowing snow as an interaction between snow characteristics and this local wind, and to estimate the corresponding fluxes in a common way with SYTRON1 in order to take advantage of its daily monitoring.
To adapt the scheme of crystal modification of the drifted snow after deposition as in SYTRON1.
To define a new redeposition scheme and the corresponding rates.
To elaborate a validation process based on remote measurements.
All these points will be addressed below, while the detailed formulation is given in Reference Durand, Guyomarc’h and MérindolDurand and others (2001) and Reference Guyomarc’h, Durand, Mérindol and LecorpsGuyomarc’h and others (2002). Concerning the last point, all the numerical simulations are performed around an experimental observation site where observations have been made for >10 years. During these years our team became very familiar with this site. The site as well as its climatology is described by Reference Guyomarc’h, Durand, Mérindol and Naaim-BouvetGuyomarc’h and others (2001) and is shown in Figure 1a and b. It is located at 2700 ma.s.l. near the ski resort Alpe d’Huez in the Grandes Rousses massif and is characterized by significant snowdrift events. Several sensors have been set up here and in the surrounding area, in order to observe and quantify the amount of drifted snow both in the air and on the ground. However, the large variability of the local topography at very fine scales usually makes comparisons with the models difficult. Changes in the shapes of the drifted crystals have been investigated both at the field site and in the cold laboratory. This allowed the determination of empirical laws of crystal modifications which are used by SYTRON1 and SYTRON2. A brief review of some indications can be found in Guyomarc’h and others (Reference Guyomarc’h and Mérindol1991, Reference Guyomarc’h and Mérindol1995).
5. Wind Modelling
The non-hydrostatic weather model Meso-NH is developed in cooperation by the Centre National de Recherches Météorologiques, Météo-France, and the Laboratoire d’Aérologie, Centre National de la Recherche Scientifique, France (Reference LaforeLafore and others, 1998). This model allows numerical simulations of the fine atmospheric motions ranging from large meso-alpha scales down to the microscale, using a comprehensive physical package.
For our application, we performed 20 runs for different dates with snowdrift events or heavy winds at our test site. Every run consisted of a simulation with 12 km horizontal resolution. This run with a new set of physiographic data, namely horizon mask, topography, soil and vegetation characteristics, albedo and emissivity, provided the initial and lateral conditions for a second run at 1.2 km resolution. A third run with 600 m resolution and nested in the previous one, provided the wind field for the particular date (Reference Mérindol, Durand and Guyomarc’hMérindol and others, 2000). Due to the complex and steep topography of our zone, it was not possible to achieve a finer mesh with the present version of the model. However, this limited sample of meteorological data covers most of the typical meteorological situations over the French Alps and represents a valuable dataset for tuning and validating simpler methods.
Besides these reference simulations, which cannot be run in real time, we have developed a simpler model suited for local application in an operational framework, covering the range 600–45m. The model, called SAMVER, is based on the conservation of the potential vorticity and divergence on isentropic surfaces close to our site of interest (Reference HoltonHolton, 1979). This model is initialized by the analyzed SAFRAN outputs (Reference Durand, Giraud, Brun, Mérindol and MartinDurand and others, 1999) representative of the massif scale, and aims to adapt these large-scale fields to a finer topography of 45 m resolution, using several known simplifying assumptions. The main advantage of the model is its ability to deliver routinely (every hour) an approximation of the relevant winds, which can be used for snowdrift computations. However, fine-mesh effects are often smoothed or under-evaluated.
We recognize the limitations of such a simplified approach, hence the model output is statistically corrected after running according to the topography used.
It is well known that topographic effects produce a turn in wind direction at small scales. Thus we have applied the formulation of wind deflection proposed by Reference RyanRyan (1977), and quoted and used by Reference Purves, Barton, Mackaness and SugdenPurves and others (1998) for inclinations <45°:
where Fd is the wind diversion, sd is the inclination (%), A is the slope aspect and θ is the wind direction.
The second set of corrections concerns the SAMVER wind velocity. The same approach as that of Reference Liston and SturmListon and Sturm (1998) is used but applying two ranges of scales, 600 m and 45 m. These corrections are based on the topographic variations at these two different scales, represented by the topographic slopes Ωs and curvature Ωc in the wind
direction, and are discretized as:
where W is an empirical weighting factor for the wind velocity, and γs and γc are constant to define at different spatial scales, respectively.
The SAMVER velocity correction at the 600 m scale is based on comparisons with the Meso-NHresults over the 20 previously studied situations, where numerical results from both models are available. The Meso-NH wind fields are considered the best possible estimation at this scale for a computational area of about 3 × 3 km2 and are henceforth used as reference fields to compute the appropriated constants, γs andγc, at this scale. An indication of the initial performance of both models can be given by their respective comparisons with the observed wind velocity in the laboratory, where Meso-NHexhibits a correlation factor, R, of 0.8 (based on the 20 runs). The corresponding initial value for SAMVER is only 0.65 before correction.
In a second pass, a new correctionwith a finer-mesh topography is performed. Here the parameters used, γs, γc, are derived from local field observations and lastly hand-tuned. The wind finally obtained is then used in the form of the shear velocity, as is done by Reference Li and PomeroyLi and Pomeroy (1997), while linking the wind transport to the measured wind. An illustration of the wind field issued from SAMVER is presented in Figure 3: the map is centred at the location of the instrumented site of Col du Lac Blanc (north is up). The contour lines are in steps of 100 m and show how the instrumented site is located within a natural channel, with the Dôme des Petites Rousses (2800ma.s.l.) at the west and the Chaîne des Grandes Rousses (>3000ma.s.l.) at the east side.

Fig. 3. Representation of the fine-mesh topography at the Col du Lac Blanc test site and the wind-field output from the SAMVER model. Axis units are gridcells, corresponding to a unit area of 45 × 45 m2 and a total area of 2700 × 2700 m2.
6. The SYTRON2 Model
6.1. Presentation
SYTRON2 exhibits many differences from SYTRON1. Unlike the latter with its two“fictive” locations, SYTRON2 is a two-dimensional model which runs at finer scale on a more realistic topography, using a digital elevation model (DEM) with a grid resolution of about 45 m.Within the 3 × 3km2 computational area, one can observe different aspects, slopes and elevations, which will lead to a complex interaction of the different phenomena of snow transport, erosion and accumulation.
Two new operators have been added to STYRON2 to describe the relations for the transport mechanism and the accumulation rate. The rest is common with SYTRON1 which is presently in operational use and is checked daily. This constant checking process allows a common upgrade and improvement of new operators through a distinct validation of the two models with the measurements at the instrumented site. SYTRON2 can be seen as a highly simplified version of models like those of Reference GauerGauer 1998a, Reference Gauerb, Reference Gauer2001), Reference Liston and SturmListon and Sturm (1998) or Reference Lehning, Doorschot and BarteltLehning and others 2000a, Reference Lehning, Doorschot, Fierz and Raderschall2002), but with the ability to simulate drifting-snow events at different locations inside the massifs, where the SCM chain operates, in near real time. The flow chart of these models is presented in Figure 2.
6.2. Operators
As previously mentioned, an extreme simplification has been chosen in the design of the model in order to be able to produce results, at nearly real time and with a moderate amount of computer time. The only variable considered is the averaged mass m (kg) of drifting snow in a mesh cell. This crude approach of one averaged layer does not allow a distinction to be made between the different transport modes, saltation, creep or suspension. The temporal mass evolution is treated by a classical mass-balance equation which guarantees the horizontal conservation of the drifted snow mass by the transport operators and also involves the other variation operators for erosion and accumulation:
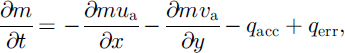
where ua (m s-1) and υa(m s-1) represent the horizontal particle advection components, in the x and y direction, and qacc (kg s-1) and qerr (kg s-1) are the accumulation and the erosion rates, respectively. The operator qerr is the same as used in SYTRON1 (for a complete description, see Reference Durand, Guyomarc’h and MérindolDurand and others, 2001) and feeds the moving mass m and the losses by sublimation at once. As the mesh size is about 45 m, the corresponding time-step in the Eulerian numerical scheme used is <2 s according to the Courant criteria. This formulation for the erosion does not take into account any interaction between the individual drifted crystals nor any turbulence effects, and only the horizontal advection is treated without vertical influence. The wind-advection scheme has to be representative of the particle velocities in the different transport modes at different heights according to the respective concentrations, even if the main transport occurs in saltation (see Fig. 1b). Here, the advection velocity can be considered almost constant (Reference Pomeroy and GrayPomeroy and Gray, 1995). The wind advection used here is a vertically averaged quantity linked to the ambient meteorological conditions. It is practically derived from the corrected-SAMVER velocity (u and v) field through the crude relationship:
with k = 0.35 derived from our field observations. A similar approach, but restricted vertically to the saltation layer, has been used by Reference GauerGauer (2001) with k = 0.58. A lower value of k is likely in our case, as we consider a larger vertical layer than Gauer. Higher wind speed results from including the suspension layer, yet most of the snow is transported within the saltation layer, so a lower value of k is a realistic assumption when considering the vertical distribution of snowdrift.
The accumulation operator qacc differs from those of SYTRON1. As no explicit particle-settlement velocity can be easily derived, it has been formulated in a probabilistic manner in assuming that, from equilibrium conditions, 95% of the drifted snow was redeposited after transport over a fetch distance, ![]() of about 1200 m with a mean horizontal wind-transport velocity
of about 1200 m with a mean horizontal wind-transport velocity ![]() of at least 15ms-1. These values are calculated following standard approaches in meteorology for the deposition of advected scalars. The probabilistic formulation is similar to that used in other studies of snowdrift, and the ratio
of at least 15ms-1. These values are calculated following standard approaches in meteorology for the deposition of advected scalars. The probabilistic formulation is similar to that used in other studies of snowdrift, and the ratio ![]() is in the range of values found in the literature (Reference TakeuchiTakeuchi, 1980; Reference Liston and SturmListon and Sturm, 1998; Reference Essery, Li and PomeroyEssery and others, 1999). The actual values used in this work are the best fit to previous, unpublished experimental studies using snow marked with colour tracers at the Col du Lac Blanc test site. For lower wind values the fetch distance is reduced proportionally. This fetch distance gives only a mean composite instantaneous evaluation of the deposition rate for a given wind value and is thus characteristic of the distance after which a crystal can no longer be mobilized by the wind due to the changes undergone in shape and density. This formulation partly compensates for the lack of vertical velocities in Equation (3). All the current numerical values are not finally fixed at the moment and still undergo a process of field validation. The presently used form is:
is in the range of values found in the literature (Reference TakeuchiTakeuchi, 1980; Reference Liston and SturmListon and Sturm, 1998; Reference Essery, Li and PomeroyEssery and others, 1999). The actual values used in this work are the best fit to previous, unpublished experimental studies using snow marked with colour tracers at the Col du Lac Blanc test site. For lower wind values the fetch distance is reduced proportionally. This fetch distance gives only a mean composite instantaneous evaluation of the deposition rate for a given wind value and is thus characteristic of the distance after which a crystal can no longer be mobilized by the wind due to the changes undergone in shape and density. This formulation partly compensates for the lack of vertical velocities in Equation (3). All the current numerical values are not finally fixed at the moment and still undergo a process of field validation. The presently used form is:
with
and
where ω is a large-scale vertical topographic forcing factor whose mean value along the fetch distance is assumed to be zero and δ is the topographic slope in the flux direction. A similar formulation of the deposition governed by the shape of the terrain can be found in Reference Föhn and MeisterFöhn and Meister (1983). α is estimated based on the previous redeposition hypothesis by integrating a limited form of Equation (3) over the fetch distance assuming a constant horizontal speed
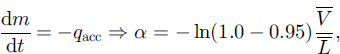
while the constant β has been estimated to be 1.0 (sm-1).
Contrary to the Eulerian scheme used for the mass-transport processes, a Lagrangian method is used to determine the new morphological characteristics of the accumulated snow for each gridpoint at every time-step. It is performed by identifying the starting point of the moving crystals, then integrating the different features over the appropriate fetch distance and finally modifying these averaged characteristics. The algorithm aims at making a new drifting crystal which is closer to a small rounded grain than its previous shape. This transformation is not obtained in one time-step and can take some time. As described in Dur-and and others (2001), the dendricity of the fresh snow decreases and the sphericity increases according to the wind velocity during the transport. When the crystal has undergone some metamorphism, it will decrease in size and increase in sphericity, always as a function of the wind velocity during the transport. These operators are based on observation of the drifted crystals, done at the instrumented site for many years, as well as on the densification mechanisms presented in Reference Durand, Guyomarc’h and MérindolDurand and others (2001).
At each gridpoint and time-step, the deposited snow is then added to the snow bed by aggregation to the first layer, or through a new layer if the amount is large enough. In case of snowfall, fresh snow is simply added to the snow mass in movement and treated as eroded snow. This allows a deposition of the fresh snow suited to the wind and topographic conditions.
All these formulations have an implicit self-limitation: the transported snow is less subject to a new drifting effect during the following hours because it underwent some crystal changes, which decrease the corresponding snow-drift-ability index and thus the transportability. Over an area of 60 × 60 gridpoints, 1 hour of numerical integration takes about 2 min of computer time in an HP J282 UNIX workstation using a constant hourly velocity field.
6.3. Initializations and downscaling procedures
The only meteorological and snow conditions routinely available are those provided by the SCM on an hourly basis and at the massif scale. As presented by Reference Bouvet-Naaim, Durand, Naaim, Guyomarc’h, Michaux and MérindolBouvet-Naaim and others (2001), this information is not sufficient because snow-transport phenomena cover a larger range of spatial scales, including smaller scales, with complex interactions. Hence, the described models, SAMVER and SYTRON2, have to be fed with appropriate small-scale information derived from larger scales by suitable downscaling procedures, which are mainly issued from statistical–dynamical methods and are always under evaluation.
SAMVER needs only an initial air temperature and wind field to start the run. The initial temperature values are derived by linear interpolation between the main SCM elevations and expositions at each gridpoint. Although this assumption is adequate for the air temperature, it is insufficient for the wind field. Presently, it is very difficult to obtain a realistic small-scale estimation of the wind field in mountainous conditions because it exceeds in many respects both the computer capacities and the state of the art, especially regarding the turbulence formulation. Therefore, the initial velocity field (two wind components) is obtained in two steps: first, a projection on the gridpoints according to their relative exposition from the SCM wind-transport velocity and direction (noted Wt in Reference Durand, Guyomarc’h and MérindolDurand and others, 2001) is derived, and secondly, a global minimization of the divergence over the whole domain is applied. The previously described final corrections with fine topography can be considered as downscaling operators.
SYTRON2 initially needs a complete description of the snow profile on each gridpoint in terms of stratigraphy, density and temperature, which implies defining some interpolation operators between the available SCM profiles. Snow professionals all know how difficult a rigorous comparison between two profiles is. The SCM profiles are firstly simplified by aggregating coherent daily snow layers according to the international classification (Reference ColbeckColbeck and others, 1990) in order to better identify the corresponding homogeneous layers between the different SCM profiles. In a second step, the different layers are interpolated at each gridpoint profile according to the exposition, aspect, elevation and a distance function of the grain types. This distance is the same one used by Reference Lehning, Fierz and LundyLehning and others (2001) for comparing different snow profiles. When the SCM profiles exhibit characteristics that are too different in terms of crystallography, several small layers, representative of these inhomogeneous features, are superposed in the gridpoint profile.
6.4. Limitations of the model
The new approach still has numerous limitations. Beside the simplicity of the scheme, we should mention the constant horizontal wind velocity during the 1 hour time-step and the neglect of the turbulent entrainment of snow, which has a stabilizing effect with subsequent damping of turbulence (Reference Wamser and LykossovWamser and Lykossov, 1995; Reference BintanjaBintanja, 1998; Reference Gallée, Guyomarc’h and BrunGallée and others, 2000).
At present, one of the main limitations is the impossibility of following drift events over the entire winter season. It is also impossible to feed back the new profile information available at the small-scale grid into the large-scale system referenced in terms of massif/elevation/slope/aspect. Thus, it is only possible to simulate a drift event without taking into account any information from the previous drift events and using only an initial state adapted from the larger scales. However, the main limitation remains the large simplification of the scheme. We are fully aware of the need to improve the mechanisms represented in parallel with a better initialization, since large discrepancies in the initial conditions could imply unacceptable gaps even in a more sophisticated model.
7. Example of Modelling Results: Morning of 31 January 2003
This date was characterized by a recent small snowfall (10 cm) under light winds, up to 6.5 ms-1, and mild temperatures. The transition line between snow and rain was at around 2600–2700ma.s.l. This meteorological situation illustrates well some of the previously presented operators and the ability of the model to discern snow driftability. The maps in Figure 4 cover the same area as in Figure 3, with the same 45 m mesh. Figure 4a shows the variation of snow depth due to the drift event (green colours represent the accumulations and brown the erosions with scales in the range from -5 to +5 cm). Figure 4b exhibits the final surface crystal characteristics in the Crocus formalism (Reference Brun, David, Sudul and BrunotBrun and others, 1992).

Fig. 4. Snow-depth field deduced from the SCM snow profile on 31 January 2002 at 06 UTC and subjected to the effects of the SAMVER plotted wind field (darts) for several hours. (a) Variation of the snow depth during the drift event; (b) the final crystal shape of the first layer of the snowpack after this event. The figure shows the ability of the model to discern snow type and its driftability. To the west of the image, on the lower section below 2700 m, precipitation was heavy snow or rain, and no drift occurs. Only lighter snow at higher altitude has been transported.
No drift occurs below 2700 m. This is due both to the initial conditions, corresponding to rounded grains (pink and red colour), and to the fact that below this altitude new precipitation occurred as rain. Some rounded grains are also visible at higher elevations on southern aspects due to radiative effects and light wind erosion. The variations in the shape of the fresh snow crystals (in green) are mainly due to the wind transport.
One can thus see how the snow cover has been modified according to the expositions through the action of the different snow-transport operators. Presumably, the south-south-west wind induces a transport from the southern windward aspects to the northern leeward ones through the action of the different fluxes involved, as described. One can recognize such patterns in Figure 4a at different locations at high elevation and also at the centre of the area, which exhibits a large dipole erosion/accumulation. One can also notice a certain variability of the snow-depth field in all aspects due to several small topographic features.
8. Field Validations
8.1. Comparisons with local observations
Different approaches are followed to test the performance of the model and its ability to simulate real events. Two automatic weather stations permanently record wind speed, wind direction and snow depth at the Col du Lac Blanc observation site (Fig. 1). A network of 18 snow poles is regularly monitored to assess the height variations of the snow-pack along a north–south transect with varying slopes and aspects. This task, already presented for one season in Dur-and and others (2001, Fig. 2), has been continued for five winter seasons (not presented here) and aims to provide information for the tuning of the operators common to SYTRON1and SYTRON2.
8.2. Photographic survey
A remote-sensing approach using oblique digital photography is employed to monitor the spatial variations of the snow cover throughout the winter season. Different works have been undertaken to diagnose snowdrift effects (accumulation and deposition areas) through the patterns of the picture. A simple example of the raw phenomena is illustrated in Figure 5 which represents the northern wind situation from 6 February 2003. Figure 5a shows a view of Col du Lac Blanc from the northwest (located at the centre of Figure 3 and 4, with the Dôme des Petites Rousses on the right), while Figure 5b represents the modelled snow-depth variation at the same date with the same colour code as in Figure 4 (but different depth scale). Both panels exhibit a large erosion area on this windward slope with a maximum modelled value of about 15 cm. The systematic survey and treatment of this information is in progress throughout the season.

Fig. 5. Comparison between photograph (a) and modelled snow-depth variations field (b), on morning of 7 February 2003 on the northern slope of Col du Lac Blanc. Both panels exhibit the same large-scale erosion area due to the effects of a previous northerly wind.
8.3. Albedo comparisons
Underlying theory and assumptions
Many snowdrift events result in variations of the snow layer of the order of a few cm d–1 according to one run of the model SYTRON2, when the total snow transport is averaged over the whole surface of the gridcell (about 2000 m2). Although precise laser altimetry would be suitable to detect this variation, its application to a large area is impractical. Differential interferometry has proven useful to detect centimetric variations in ice depth over glaciers, but given the cold, dry conditions and low densities of the fresh snow layer, evaluating the returned radar signal is likely to present problems, and besides the costs of high-temporal-resolution monitoring would be prohibitive. Therefore it is necessary to find a tool easy to deploy, of low cost and ready for use at the required date and time.
The relationship between snow-grain characteristics and albedo has been described by several authors (e.g.Reference Wiscombe and WarrenWiscombe and Warren, 1980; Reference Dozier, Schneider and McGinnisDozier and others, 1981; Reference Fily, Bourdelles, Dedieu and SergentFily and others, 1997; Reference Nolin and DozierNolin and Dozier, 2000). Wind transport of snow results in mechanical modifications of the snow grain, and snow grains are differentially transported according to their characteristics (Reference Guyomarc’h and MérindolGuyomarc’h and Mérindol, 1991, Reference Guyomarc’h and Mérindol1995; Reference Guyomarc’h, Durand, Mérindol and LecorpsGuyomarc’h and others, 2002). Hence, a modification of the reflectiveness of the snow layer can be expected during a snowdrift event, which could be detected using optical and near-infrared detectors. Research is ongoing, and the first results for the winter 2002/03 campaign are presented here; a more detailed study and the full theoretical background will be presented in a future paper.
Methodology
Oblique digital photographs of the study site were taken from different points and georeferenced to a DEM of the area. The georeferencing process is explained in detail in Reference CorripioCorripio (2002), and consists of applying a viewing transformation to the DEM according to the position, viewing direction and focal length of the photographic image. The result is projected into perspective and scaled according to the resolution of the digital image, resulting in a “virtual” photography of the DEM that can be compared to the actual photography of the area. Finally, a mapping function between the perspective position of the DEM gridcells and the photographic pixels establishes the exact location of every point in the image (Fig. 6).

Fig. 6. Georeferenced map of reflectance values from digital photographs taken from Pic du Lac Blanc (at the lower right of the image) in the direction of Col du Lac Blac (at the lower centre left of the image). This map was acquired after the correction for terrain parameters, atmospheric transmittances and the ratio of direct to diffuse radiation produced in Figure 7.
Once the photograph is georeferenced, the reflectance values are normalized according to the viewing geometry, the angle of incidence of sun rays on the slope, the ratio of direct to diffuse radiation, the atmospheric transmittance between the pixel location and the position of the camera, and the effect of radiation reflected on the surrounding slopes. The final result is a map of normalized reflectance values, or relative albedos, that can be compared to the albedo derived from the snow-grain types predicted by the model, which is calculated following the formulation used in the Crocus model (Reference Brun, David, Sudul and BrunotBrun and others, 1992). This photographic technique for albedo estimation has performed well in similar alpine environments according to previous experiments performed by one of the authors. It is also worth noticing that in terms of albedo at high-altitude mountain sites, Crocus is the best-performing model in a recent intercomparison study (Reference EtcheversEtchevers and others, 2004).
First results
Figure 7a and b show the results for the photographically derived and the model-estimated albedo, respectively, for 18 February 2003. Both images are for a grid resolution of 45 m. The comparison is qualitatively satisfactory, although there are problems resulting from sub-grid variability in reflectance values and snow-accumulation patterns that are inherent in the use of discrete mathematical representations of topography in the form of DEMs.
The large areas of lower and higher albedo are similar, both in the simulations and in the photographic estimation. Areas of maximum albedo in the photography tend to be near to non-visible areas (black shapes in Fig. 7). These regions correspond to zones where the incidence angle of the sun is almost tangential. This results in lower insolation and therefore slower snow metamorphism, maintaining a higher albedo. At low illumination angles, however, the photographically derived albedo should be modified according to appropriate bidirectional reflectance distribution functions, and the margins for error increase. These first results reveal that the technique has a good potential applicability for the validation of spatial models.

Fig. 7. Albedo estimated from photography (a) and according to snow-grain characteristics modelled by SYTRON2 (b) on 18 February 2003 at Col du Lac Blanc. Map (a) is derived from the image in Figure 6 after correction for terrain parameters, atmospheric transmittances and the ratio of direct to diffuse radiation. The colour code does not represent absolute values but a relative gradation from lower values (blue) to higher ones (red).
9. Future Work
Several improvements to the different models are in progress. The SAMVER model is being improved by the addition of new vertical layers which will lead to a more precise initial wind-velocity estimation and a possible use of vertical velocities in both the advection scheme and the erosion/accumulation operators. In SYTRON2, we will separate the different transport modes, saltation, creep and turbulent diffusion, with distinct advections and mass exchanges between them.
Future work for the validation includes the use of spectral filtering to take advantage of the variability of snow albedo in the near-infrared region of the spectrum and the application of digital image processing for image segmentation and pattern recognition (e.g. sastrugi) that can be related to areas of erosion deposition and different degrees of transport.
10. Conclusion
This work continues more than 10 years of experiments and archives from the instrumented site at Lac Blanc. We tried to model the observed wind-transport phenomena while keeping in mind the necessity to build a system able to run operationally and be coupled to the SCM chain.The differences in length scales due to the phenomena involved, the strong forcing of the topography, and the difficulty of obtaining a realistic wind field, make this approach difficult and challenging.
This objective has been attained for SYTRON1 and is in progress for SYTRON2. For the latter, we still have to develop new scientifically based improvements and to take better account of the energetical evolution of the snowpack. The first results are encouraging and show the ability of the models to capture some of the main observed snow features. Among these correct results are the localization of areas of snow erosion and deposition (Fig. 4a); the ability to distinguish between snow grains that are likely to be transported and those which are not, or what we call driftability (Fig. 4b); the adequate coupling with the snow surface layer modelled by Crocus; the general intensity and direction of winds at the surface (Fig. 3); and the ability to simulate snow-grain modification and its effects on the relative variation of snow albedo (Fig. 7). The validation process has opened a new field of remote investigations of the surface snowpack characteristics; it will be continued and developed for other applications.
This objective has been attained for SYTRON1 and is in progress for SYTRON2. For the latter, we still have to develop new scientifically based improvements and to take better account of the energetical evolution of the snowpack. The first results are encouraging and show the ability of the models to capture some of the main observed snow features. Among these correct results are the localization of areas of snow erosion and deposition (Fig. 4a); the ability to distinguish between snow grains that are likely to be transported and those which are not, or what we call driftability (Fig. 4b); the adequate coupling with the snow surface layer modelled by Crocus; the general intensity and direction of winds at the surface (Fig. 3); and the ability to simulate snow-grain modification and its effects on the relative variation of snow albedo (Fig. 7). The validation process has opened a new field of remote investigations of the surface snowpack characteristics; it will be continued and developed for other applications.
Acknowledgements
We are grateful to the management and people of the Safety Service of Alpes d’Huez, who help us maintain the observation site. Special thanks to P. Pugliése, who is in charge of the instrumentation of the site, to D. Ramalingdom, from Centre Universitaire des Sciences et Techniques (CUST), Clermont-Ferrand, France, who did the preliminary work during his stay at CEN, and to D. Charlieu and D. Lecorps for their help with photographic treatments and techniques. We thank the editors and the anonymous referees for their detailed and meticulous revision of the paper’s form and content, and for their helpful suggestions, which greatly improved the final version. We are also indebted to friends and colleagues for their comments and their suggestions.





