Introduction
Characterization of physical properties of snow, in addition to temperature and snow density, requires parameterization of the configuration of the ice matrix of snow―“snow structure”. The characteristics representing a rock (snow) structure are: (1) size, form and characteristics of surface of the particles constituting the matrix; (2) positioning of the particles relative to each other and their interdependence; (3) type of bonding between the particles. In addition, it had been found that in granular snow the arrangement of particles corresponds to fragmental units (10–102 grains per unit), with structural properties of these fragments departing quite far from the mean properties of the corresponding snow layer (Reference GolubevGolubev, 1987;Reference Takeuchi, Nohguchi, Kawashima and IzumiTakeuchi and others, 1998). Thus, the normally required information about averaged properties for the snow horizon (layer) is only possible when empirical analysis involves about 104 snow grains.
Detailed study of such a large system is possible (Reference SchneebeliSchneebeli, 2002), but is complicated and cannot avoid certain generalizations about the ice-matrix arrangement (Reference Lundy, Edens and BrownLundy and others, 2002). Such generalization can be made in the form of a model that adequately represents necessary observable mean structural parameters. This then allows analytical estimation of the main properties of snow and their evolution as a result of snow metamorphism.
The model of regular grain packing of snow presented in this paper is based on the results of microphotographic and cold-room microscopic analysis of natural fine-, medium-and large-grained granular snow. The data obtained support the possibility that the model can approximate the ice-matrix configuration as a regular lattice of near-spherical ice grains connected by rigid ice bonds (necks). Characterization of certain ice-matrix parameters, such as the specific surface area of snow, would require other ways of generalizing the ice matrix (Reference Grenfell and WarrenGrenfell and Warren, 1999). However, the possibility of using the present model to estimate a number of other physical–mechanical characteristics of snow has been checked and reported previously (Reference Golubev and FrolovGolubev and Frolov, 1998, Reference Golubev and Frolov2000).
Model of the Snow Structure
The model of regular grain packing assumes that grains with mean diameter Dm are uniformly distributed in space and are connected by bonds with length l and diameter d. The distance between centers of the contacting grains is L = Dm + l, and the coordination number (the mean quantity of bonds per a grain) is j (Fig. 1).

Fig. 1. Grain-packing schemes with j = 3 (a), j = 4 (b) and j = 6 (c).
For such a construction, the density of snow, ρsn (kgm–3), can be represented as:

where ρi is the ice density (kgm–3), Vg and Vb are the volumes of an average grain and of an average bond respectively (m3) and Ng is the number of grains per unit of volume (m–3).
Number of grains per unit of volume
For a known snow density the number of grains per unit of volume can be related to the grains’ sizes and form. Approximating the snow grains as equal ice spheres ofmean diameter D = Dm, and assuming the bonds to be of cylindrical form with diameter d, where the grain and bond volumes are given by Vg = πD3/6 and Vb = πd2l/4 respectively, the number of grains per unit of volume becomes:
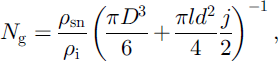
or, introducing the dimensionless parameters of rigidity (b = d/D) and of looseness (k = L/D) of the snow structure:

where the term in square brackets characterizes the relative volume of the bonds.
Mean grain-size and the size of an average grain
Since the actual form of the snow grains is not spherical, the diameters of grains estimated in different directions may vary up to 2.5–3 times. Statistical analysis of the results of the authors’measurements shows that for natural granular snow for most grains the ratio of maximal diameter (Dmax) to minimal (Dmin) is not more than 2 and has an average value of 1.5 (Fig. 2). Mean grain-size for the ith grain (Di) was determined from Di = (Dmax + Dmin)/2 and in most cases could be approximated by Di = 1.25Dmin. When other methods of estimation are used, such as measuring the size of a grain along x/y axes in a randomly oriented rectangular system of coordinates, Di = Dx + Dy) /2 for a grain can differ by 15–25% from those based on Dmax and Dmin. However, the mean diameter for an assembly of grains was practically the same regardless of the method (Fig. 3).

Fig. 2. Relationship between Dmax and Dmin in granular snow.

Fig. 3. Relationship between the mean grain-sizes Di determined from Dmax and Dmin and from Dx and Dy.
The size of an average grain of the assembly can be determined by:

where Di is the mean diameter of an ith grain and n is the number of grains. In granular snow the values of Dm can be estimated with 3%confidence for n ≥150.
Form of grains
Comparison of the grain-sizes determined by measurements in a randomly oriented rectangular coordinate system with measurements of the areas and perimeters of the two-dimensional (2-D) projections of the grains confirms the similarity of the snow grains’ forms to spheres. Figure 4a shows the histogram of the values of the normalizing factor β1 for measured areas (Si) of the grains’ 2-D projections and Di in fine-, medium- and large-grained snow: Si = β1(Di/2)2, where Di was estimated as the average of Dmax and Dmin. The estimated values of β1 varied from 1.8 to 4, with an average of 3.05 (Fig. 4).

Fig. 4. Histograms of the experimentally determined values of β1 = Si/(Di/2)2 (a) and β2 = Pi/Di (b) in granular snow.
The normalizing factor (β2) for the relation between perimeters (Pi) of the 2-D projections of grains and Di (Pi = β2Di) varied between 2.8 and 3.8, with an average of 3.25 (Fig. 4b).
The deviation of β1 and β2 from π is related to faceting of the crystals in snow and to contingency in values of Dx and Dy. The estimated values (Fig. 5) are close to those of a rectilinear hexagonal polygon. Thus, the 2-D projections of the grains can also be interpreted as hexagons. However, since the statistical-mean deviation of β1 and β2 from π is relatively small, for a large assembly of grains the grains may legitimately be treated as spheres.

Fig. 5. Values of β1 and β2 for rectilinear polygons.
Distances between the grain centers
Loose packing of grains in snow may correspond to different relative positioning of the grains. The main factor determining the grain packing is the distance L (Lm) between the grains or the looseness parameter k(km = Lm/Dm). Bonds are present in snow when km>1. For km<1, the prolonged bonds have to be absent and the spherical grains must be deformed at their contacts.
According to our observations, bonds, as a formation having certain dimensions, do not have specific crystal lattice orientation different from both the connected grains. There is a real contact (point or area) between neighboring grains (Fig. 6). The phase-change processes, as well as volumetric and surface diffusion, result in a form characteristic of so-called necks. Thus, in estimating the distance between the snow grains, their non-spherical form must be taken into account, and use of l as a part of the distance between centers of neighboring grains L should be avoided.

Fig. 6. Grains-contact scheme.
The most problematic part of measurements and modeling is the position of the center of a grain. If an axis x is directed along a bond, while axis y lies in the area of a contact between grains, the measurements of the dimensions of the contacting grains (i and i + 1) in the direction of the bond ![]() and perpendicular to that
and perpendicular to that ![]() would provide
would provide ![]() and km = Lm/Dm = 2/(1 + α), where
and km = Lm/Dm = 2/(1 + α), where ![]() The observed values for α in snow lie between 0.7 and 1.4, with the average value equal to 1.1. This corresponds to km = 0.95.
The observed values for α in snow lie between 0.7 and 1.4, with the average value equal to 1.1. This corresponds to km = 0.95.
Since the snow grains are not exact spheres, the departure of km from 1 is related not to deformation of spherical grains or to large external forces (the latter are very rare in nature), but to different types of contacts between polyhedral (faceted) grains: plane–plane, plane–vertex, plane– edge, etc. The looseness parameter k for hexagonal prisms and rhombododecahedrons varies, depending upon packing, from 0.85–0.90 for dense packing to 1.12 for equally possible point, line and area contacts, and up to 1.3 for allowed vertex–vertex or vertex–edge contacts only (Fig. 7). This is the same range of values as observed in snow.

Fig. 7. Relationship between the looseness (k) and the rigidity of structure (b) for spheres (I), rhombododecahedrons (II), rectilinear hexagonal prisms (III) and cubes (IV).
The geometry of the contacting faceted figures allows a value of L in the range from the contact type vertex–vertex to the contact type plane–plane (from k > 1 to k < 1) corresponding to a particular area (S) and diameter (d) of a contact. Laboratory observation has proved that it was possible to estimate Lm based on either dm or ![]() and
and ![]()
Cordination number
The observation of the coordination number in natural snow is not only difficult because of uncertainties in the accuracy of transforming 2-D images into a three-dimensional (3-D) structure, but is also complicated by high structural variability among the fragment units constructing the snow. Thus, a more reasonable way of estimating the coordination number of snow involves the modeling of grain packing based on the snow density, Lm and Ng. This approach was previously used in the form of relationships between the coordination number and either snow density or the void fraction (Reference Arons and ColbeckArons and Colbeck, 1998). In the model of regular packing of grains, each coordination number corresponds to a certain type of relative grain positioning in the space and type of packing, thus allowing incorporation of the dependence of the coordination number on grain dimensions.
For the close packing of equal spheres (j = 12), the distances between the neighboring rows of spheres in a 3-D coordinate system (a, b, c) are equal to: a = L, ![]()
![]() The number of spheres in the unit of volume is:
The number of spheres in the unit of volume is: ![]() For the non-dense cubic packing (j = 6): a = b = c = L, Ng = L-3. For tetrahedral packing (j = 4):
For the non-dense cubic packing (j = 6): a = b = c = L, Ng = L-3. For tetrahedral packing (j = 4): ![]()
![]() The minimal possible coordination number for a symmetric 3-D construction from grains connected by rigid bonds is j = 3. For such packing:
The minimal possible coordination number for a symmetric 3-D construction from grains connected by rigid bonds is j = 3. For such packing: ![]() Ng = L3(8/15)3.
Ng = L3(8/15)3.
The general form of the relationship between Ng and L can be expressed as:
where the parameter A depends on the type of packing. Figure 8 presents the relationship between the parameter A and the coordination number j. The fastest increase of A with increasing j corresponds to 3 < j < 5, and in this range the increase in the number of spheres per unit of volume is maximal, with a relatively small increase in the coordination number. If equal spheres are assumed for the snow grains, the mass of a sphere is m = ρiπD3/6, and the snow density, depending upon the grain packing, can be determined as:

Fig. 8. Relationship between the packing parameter A and the coordination number j.

Since the parameter A is a function of the coordination number, data on snow density and on looseness parameter k allow unique characterization of the coordination number j. Figure 9 shows the densities formed by spherical ice grains with different values of k and different types of regular packing. For k = 1 (contacting spheres) the maximal possible snow density is expected to be 680 kgm–3 (j = 12). However, when the bonds are accounted for, the same density can be reached with a much lower coordination number (Fig. 9). This result is in much better agreement with the coordination numbers observed in natural snow by the authors (Fig. 10). For the most common case of natural snow (3 < j < 4) the snow density is not more than 310– 320 kgm-3. The density of ice can only be reached under large deformation of the spheres.

Fig. 9. Density of the modeled packing of spherical ice grains for various looseness factors k and coordination numbers j. Solid lines: not counting parameter b (based on Equation (7) and approximation of Fig. 8); dashed lines: by combination of Equations (3) and (5), with relationship between k and b taken for spheres (Fig. 7).

Fig. 10. The experimentally observed coordination number in granular snow with different snow density.
Conclusions
Snow structure can be rather accurately represented by the following parameters: (1) the mean grain-size and the histogram of the grain sizes; (2) the mean bond size and the histogram of the bond sizes; (3) coordination number and the histogram of the quantity of bonds per grain; (4) number of grains per unit of volume; (5) the dominant crystal form and the histogram of the crystal forms; (6) stereograms of the snow-crystal optical-axes orientation.
The presented model allows a structural parameter of snow that is one of the most complex to determine, the coordination number (j), to be related relatively easily to measured characteristics such as snow density (ρsn), mean grain diameter (Dm) and the sizes of contacting grains in the direction of bonds (Dx) and perpendicular to that Dy). The relationship is shown schematically in Figure 9. The logic of the estimation can also be as follows:
(a) the snow density and the mean grain diameter allow the number of grains per unit volume to be estimated (Equation (6));
(b) the mean value of the looseness parameter can be calculated as ![]() i.e from the mean grain-sizes perpendicular and parallel to bonds;
i.e from the mean grain-sizes perpendicular and parallel to bonds;
(c) the packing parameter A can be found from Equation (7);
(d) the coordination number is then determined from A as suggested by Figure 8:
The snow-structure studies are mainly directed to the estimation of the quantitative relations between the snow structure and the physical–mechanical properties of snow and their change as a result of metamorphism. Physical– mechanical properties of snow can be characterized by fewer parameters of the snow structure.
The bonds are the weakest components of the ice matrix in snow. That is why there must be a correlation between the mechanical properties of snow and the areas of the contacts between the grains in the unit of surface, i.e. the relative contact area s (Reference GolubevGolubev, 1982; Reference Golubev and FrolovGolubev and Frolov, 1998, Reference Golubev and Frolov2000):
That is why the rigidity of snow structure b = dm/Dm, based on the mean diameter of contact and the mean diameter of grains, is linked to the mechanical properties and also can serve for controlling the values of looseness parameter k, as shown in Figure 7. For contacting hexagonal prisms or rhombododecahedrons:
Acknowledgements
The authors thank R. L. Brown and M. Edens for the numerous corrections and suggestions made in their reviews, which have been incorporated into the paper.



