Introduction
The structure of snow is formed by ice grains connected with rather rigid bonds. Snow of identical density and phase composition can be characterized by different spatial arrangements and by different numbers and shapes of the grains and connecting elements — bonds. This is the reason for significant diversity in the physical properties of snow. Snow densification and diagenesis follows a considerable re-organization of the media structure-formation of a new spatial packing of grains and more and more rigid bonds between them. These processes lead to corresponding changes in the physical properties. For instance, the moduli of elasticity and strength increase at 4–5 orders from new snow to massive ice, whereas the density, thermal conductivity, permittivity and other properties increase by ten limes only. This suggests a very high sensitivity of the mechanical properties to structural changes in snow. Therefore, any structural models of snow should include the possibility of being compared with experimental data on the mechanical properties of snow. The purpose of the present work is to si udy the dry-coherent snow structural parameters changes, which determine mechanical and other physical properties of snow.
Background
The principal characteristic of snow microstructure includes the following parameters:
-
(1) Diameter of an average grain D.
-
(2) Diameterofanavcragcintcrgranularcontact (bond) d
-
(3) Coordination number of structure i.
-
(4) Number of grains per unit of volume N.
All these parameters are changing in the snow-densification process and the dominant mechanism of such transformations should be different for the medium transient stages Irom one grain-packing order to another, or the more perfect order. These transient stages should be bordered by the medium stages (densities) in which the formation of certain structure is already over and a transition to the next stage begins with another prevailing mechanism of densification. It is possible to have several such borderline structural stages in which changes of mechanical properties of snow should be Sufficiently sharp.
The critical densities 550 and 820 kgm −3 are the borderlines between snow, firn and porous ice, and arc well-known (Reference Anderson., Benson. and KinRery.Anderson and Benson, 1963). The marked changes in experimentally obtained relationships between snow density and mechanical properties of snow correspond to these borderline stages.
Reference Frolov, Fedyukin. and Yamslichikov.Frolov and Fedyukin (1996, Reference Frolov and Fedyukin.1998) observed these and some additional borderlines, corresponding to densities ~ 150, ~330 and ~700 kgm −3 when they analyzed data on acoustic and clastic properties of snow. The last one is practically coincident with the 730 kgm −3 density, which was noted by Reference Maeno.Maeno (1978). However, the structural stages of the medium corresponding to these values of density remain unclear.
Stercological and statistical methods are usually used for the study of snow structure by thin-section analysis or loose grains for estimating average sizes of the grains and the inter-grain bonds. Determination of the amount of grains per unit of snow volume is usually based on the assumption of the spherical shape of snow grains. However, one of the basic parameters, namely the coordination number of structure i (i.e. the average number of nearest neighbours, rigidly connected with a central grain) cannot be determined reliably from two-dimensional observation. This circumstance forced the models of snow structure to develop, which it was possible to subdivide into two main groups: (1) statistical models, supposing a random packing of grains, the sizes of which are identical to or correspond to some types of distributions; (2) models of regular packing, supposing a geometrically regular space arrangement of the grains.
In the first group of models, the coordination number of structure is estimated statistically and this is based on certain stereological assumptions (Reference KryKry, 1975; Gubler, 1978). The second group of models assumes existence of a prevailing type of regular grain packing with a defined coordination number and allows variations in the sizes and types of contacts and intergranular distances (Reference GolubevGolubev, 1982). The last group is more preferable for analysis of the principal regularities of snow structure and mechanical property changes.
Model of Granular-Snow Structure
The present model of granular-snow structure assumes a distinct relationship between principal structural parameters, which allow us to predict a probable change of structure and snow property in densification and metamorphism. According to this model, the grains of average diameter D are joined in a framework by rigid bonds with diameter d. The average number of the bonds-per-grain is equal to i. and the centre-to-centre distance of the contacting grains, L. At the same time, D = f(Dx, Dy) (Fig. 1).

Fig. 1. Schematic presentation of contacting grains.
Density of the ice matrix of snow ρs can be described by the following expression:

where: ρi is density of pure ice, 917 kgm−3; i is the coordination number of structure; Ng is the number of grains per unit volume of snow; l = L − D is the length of an average bond; Fg and Fb are the form factors of grains and bonds, respectively.
More detailed description of the parameters of the model is as follows:
Number of grains pet unit volume of snow
In the case of the spherical shape of grains and cylindrical shape of bonds, the form factor of grains Fg = π/6 and the form factor of bonds F= π/4. Introducing two-dimension-less parameters b = d/D, describing rigidity and k = L/D, describing friability of structure; the following expression will determine the number of grains per unit of snow volume:

where the part in square brackets with a multiplier i/2 characterizes relative volume of bonds, which may change from 1 to 6%. Usually, it will be a value of about 2%.
Centre-to-centre distance between the contacting grains
Usually there are direct contacts (point, line or area) of two grains and the cylindrical shape of inter-grain bonds is a result of the contact-zone transformation by evaporation-condensation, plastic flow, bulk or superficial diffusion.
Sometimes, a body of bond is formed by rather small grains, directly contacting with the neighbouring larger grains but it does not mean that the inter-grain bond is an ice substance with certain differences to those of the contacting-grains crystal lattice (Reference GolubevGolubev, 1982).
According to ice crystallography, the most probable grain shape for snow has to be the hexagonal prism or rhombic dodecahedron. That is why the parameter k difference from unity can be related not with deformation of the spherical grains under influence of significant external stresses (usually not observed in natural conditions) but with variations of the grains-polyhedrons contact. In this case, the centre-to-centre distances of the neighbouring contacting grains are determined by existence of area, line-or-point contact of a face-to-face, face-to-edge, edge-to-edge, face-to-vertex, edge-to-verlex and vertex-to-vertex types. Following our estimations, the factor of friability k varies from 0.85 to 0.90 at dense packing of perfect geometrical polyhedrons, up to 1.12 at a hexagonal prism or rhombic dodecahedron with equal probability of area, line or point contacts and up to 1.3 in the case of point contacts only. It is necessary io note that the mentioned range of k values coincide with experimental data for medium-grained snow (Reference Golubev, Voitkovskiy and Boltneva.Golubev and others, 1982).
Diameter of bonds d
The consideration of a polyhedron contact is related with the fact that each value of L in the whole range of the contact types (with k > 1 and k < 1) corresponds to the certain area of contact S and average diameter of contact d. Figure 2 shows the relationships between L/D and d/D obtained for contacting of faced figures of cubic shape (I), isometric hex-agonal prisms h/a = 1 (II), rhombic dodecahedrons (III) and deformed spheres (IV).

Fig. 2. Relationships between rigidity factor b = d/D and friability factor k = L/D in contacting oj geometrical figures: I — cubes, II — isometric hexagonal prisms, III — rhombic dodecahedrons, IV — deformed spheres.
The coordination number of structure i
It is supposed in the model of regular packing that the grains are regularly allocated in space according to a certain law, i.e. each grain contacts with strictly limited number ol neighbours i. The coordination number reaches the maximum value i = 2 under the most dense packing of the grains of equal size, under friable cubic packing i = 6, under tetrahedral packing i = 4.
Under the most-dense packing (i = 12), the structure parameters (i.e. the distances between neighboring grains in three main directions) are: a = L,
![]() ,
, ![]() and the number of spheres per unit volume is N= l/abc =
and the number of spheres per unit volume is N= l/abc = ![]()
In the case of not dense cubic packing (i = 6), the structure parameters a = b = c = L, and the number of spheres per unit volume is N = L −3.
Under tetrahedral packing (i =4) the structure parameters and the number of spheres per unit volume are: ![]() ,
, ![]() ,
, ![]() and
and 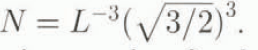
The minimal value of the coordination number for the symmetric volumetric structure of grains connected by rigid bonds is 3. Such structure can be obtained by packing of the simple figures (“snowflakes”), each consisting of from four spheres situated in one plane. Three of these spheres arc disposed in the main directions of trigonal symmetry and contact only with the central one. Snowflakes situated in one plane are not contacting with each other. An ice matrix is formed after superimposition of the next plane of such snowflakes over the present one on the distance ![]() and rotated by angle 60°. The structural para-meters of such packing of snow flakes are
and rotated by angle 60°. The structural para-meters of such packing of snow flakes are ![]() ,
, ![]() ,
, ![]() , and the number of spheres per unit volume is N = L−3(8/15)2.
, and the number of spheres per unit volume is N = L−3(8/15)2.
In the general case, the number of spheres N per unit if volume as a function of distance L can be presented as:
where: A is a parameter depending on the character of spheres packing discussed above. Figure 3 shows the relationship between A and the coordination number i The maximal increment of parameter A is observed with small values of i = 3 – 5, and, in this range, there is the fast increment of the number of spheres per unit of volume with an increase of the coordination number. Deriving Equations (2) and (3), we obtain the following equation for the snow density


Fig. 3. Coefficient A vs coordination number i.
As far as the parameter A is the function of i, the information on density of snow and parameters k and b allow us to evaluate unequivocally a coordination number of structure i (Fig. 4).

Fig. 4. Diagram oj coordination number i in dependence on snow-ice formation density p and structural parameters k and b. Points are experimental data.
Results and Discussion
For comparison of the model results with the experimental data, it is necessary to obtain the equations for some mechanical properties of the snow ice medium. Iu the model of the snow structure of any regular packing it is possible to separate chains of specific orientation formed by structural elements consisting of a grain and a bond (Reference GolubevGolubev, 1982). The chains are connected between each other cither by bonds or by the structural elements (grains 1 and 2 in Figure 5). The direction of a chain can be assigned the orientations of all its structural elements and be the same as the general chain’s direction or differ from it by some angle α. The directions of chains are: [0001] under packing with i = 3; [1100] under tetrahedral packing i = 1; [100] under cubic packing i = 6; [0001] under hexagonal packing i = 8, 10: [1100] under dense packing f = 12. With such orientation of chains, the connecting elements between them are oriented either perpendicular or close to a perpendicular direction. The number of the elements in a chain is:
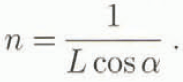
The number of chains of known orientation per unit volume is:

where ζ is the coefficient taking into account the elements connecting the neighbouring chains, ζ≥1.

Fig. 5. Scheme of chains in snow structure, Grains 1 and 2 are connecting elements between adjacent chains.
If a stress σs, less than the threshold value of proportionality in Hooke’s law is applied to the snow surface, the chains will clastically deform by the force P = σs/R. Whole, the deformation of a chain ΔH will be equal to the sum of the elastic deformations of the chain elements Δh:

The elastic deformations of the grains ΔD and the bonds Δl are:


where Ei is the modulus of the ice elasticity.
The average areas of a grain and of a bond are:

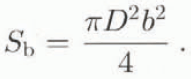
In the case of the angle α the difference between the direction of the chain and the orientation of the elements, each element and chain in general are under influence of the elastic-shearing strain caused by the tangent part of the applied force. The whole of the deformation of an element under influence of P will be:

where vI is the Poisson’s ratio.
It is assumed in the last equation that the shear modulus is determined as:
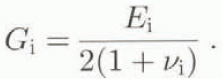
Relative elastic deformation of snow e, expressed by the elastic deformation of the elements, is:

Solving this equation allows us to obtain the relationship between the elasticity modulus of snow Es and its structural parameters:

Elastic deformation of the grains in the perpendicular direction is ΔDs = ΔDvi or ε = ViΔD/D and the relationship between the Poisson’s ratio and structure parameters is:

where c = (i − 2)/4 under i > 6 and c=1 under i ≥ 6.
The critical value of the mechanical stress following the destruction of the ice matrix of snow is dependent on the relative area of contact, i.e. quantity and dimensions of the contact bonds intersected by the possible plane of friable destruction. Assuming the strength of the bond is equal to the strength of polycrystalline ice, the Ibllowing relationships can be written:

where σi* is the strength of massive ice for a given type of strain.
Equations (15)—(17) contain the same structural parameters of snow and there are no difficulties in obtaining the relationship between these mechanical parameters. For instance, those between the snow strength and Young’s modulus can be expressed as:

The following is a brief discussion of some numerical simulation results, obtained from the present model.
As a first step, it was necessary to estimate (he most probable magnitudes of the principal structural parameters at various densities of the medium.
Figure 6 is obtained from the data in Figure 4 and shows probable intervals of the k and b values as a function of the porosity factor Kp = Vp/Vi, where Vp and Vi are the volume of pore space and volume of the ice matrix, respectively. The intervals arc established from analysis of the possible eon-tact variants of spheres, cubes, hexagonal prisms and rhombic dodecahedrons. Use of the porosity factor was found to be better for examination of the physical properties and the structural peculiarities of snow.

Fig. 6. Principal structural parameters (i, k,b) ofSttOW ire formations vs porosity factor Kp and corresponding density.
The curves presented allocate several snow-density subranges within which the laws of structural parameter changes are modified. They are displayed from analysis of the first and second derivatives. The laws of coordination number increasing during snow densification are modified for densities ≈130, ≈330, ≈550 and ≈830 km−3 and for the parameter of rigidity b for densities ≈100 and ≈730 kgm−3. Decrease in the friability parameter k becomes less intense when the density is about 550 kgm−3. Table 1 represents the probable correspondence between the magnitudes of the structural parameters and the density of snow.
Table 1. Probable correspondence between snow density and structural parameters

This correspondence was confirmed by special studies on natural snow (Reference Golubev, Voitkovskiy and Boltneva.Golubev and others, 1982: Reference Golubev.Golubev, 1987). Indicated density values (Table 1) characterize a certain dominant packing in the snow medium and appeared to be in a good agreement with the abovemenlioned critical densities determined from acoustic and clastic characteristics (Reference Frolov, Fedyukin. and Yamslichikov.Frolov and Fedyukin, 1996,Reference Frolov and Fedyukin.1998).
The terms containing the structural parameters in Equations (15) - (17) increase by 10 20 times when the density increase is 4 times (from 100 to 400 kgm−3). The final change in the modulus of elasticity and strength can be up to two orders.
In the next step, we estimated theoretically the ranges of the Poisson’s ratio v, Young’s modulus E and tensile-strength σ values. Figures 7 and 8 show the possible ranges of Ei. Vi and σs dependent on density ρsand the coefficient of porosity Kp, calculated using Equation (15), (16) and (17) with most possible values of Ei, vi and k. In Figure 7 the average values of Ei and vi from the experimental data (Reference MellorMellor, 1977; Reference Frolov and Fedyukin.Frolov and Fedyukin, 1998) are shown for comparison within the ranges of their possible values. Figure 8 shows the range of values for the tensile strength of snow obtained from centrifuging (Reference MellorMellor, 1977: Reference Golubev, Voitkovskiy and Boltneva.Golubev and others, 1982). As may be inferred, there is quite satisfactory agreement between them.

Fig. 7. Comparison of numerical calculations with averaged experimental data for snow ( solid lines) on: Young’s modulus and Poisson’s ratio (lower curve).

Fig. 8. Estimated possible ranges ( between solid lines) of tensile strength and the zone of experimental data (shown by hatching).
Concluding Remarks
The good correlation between experimental and analytical estimates of Es, vs and σs allows us to consider the proposed model of regular grain packing as sufficiently adequate for natural dry snow and useful for estimating its mechanical and other properties. The allocated critical densities, which limit the transitive stage intervals in snow densification should be taken into account in the analysis and description of densification mechanisms and changes in snow properties. The concepts and approximations presented in this paper are quite applicable for forecasting estimates of the acoustic characteristics, elastic modulus and tensile strength of dry coherent snow. The approach described here could also be used for similar estimates of thermal and other properties of snow with different structure and densities.











