Introduction
The thermal conductivity, k, is generally defined for solid materials in terms of Fourier’s law, q = −kA∇T, where q is the heat transfer rate, A is area and Τ is temperature. Heat transfer in a moist granular or porous material such as snow, however, does not take place by pure conduction as in a solid. The material under study is composed of ice, air and water vapor, each of which contributes to the overall flux. Heat may be transferred by conduction through the ice network, conduction in the interstitial pore space and water-vapor flux across the pore. In addition to these mechanisms, convection and radiation may occur, but these are not considered significant in the development presented.
In the case of composite systems such as this, an “effective” thermal conductivity is frequently used to account for all of the mechanisms of heat transfer, in lieu of the true conductivity. Empirical values of the effective thermal conductivity which have been obtained for snow most often consider only the dependence on snow density, although the influence of temperature has been considered; see for example Reference MellorMellor (1977) and Reference YenYen (1981). To the authors’ knowledge, intergranular bonding and microstructure in general have not been explicitly included in expressions for the effective thermal conductivity.
The influence of microstructure on heat and mass transfer has been addressed analytically by Reference Christon, Burns, Thompson, Sommerfeld, Jones and Orville–ThomasChriston and others (1987, Reference Christon, Burns and Sommerfeld1990), in which they consider the influence of irregular, complex grain structure on the overall process of temperature-gradient metamorphism. The effective thermal conductivity which they employ does not include the influence of intergranular bonding, however, it is compatible with the approach discussed here and could be incorporated within the framework. A development which assumes uniformly packed ice spheres is presented here to address the influence of microstructure, principally intergranular bonding, on the effective thermal conductivity of snow.
Idealized Snow Cover
The snow cover is modeled as a collection of cells, where each cell is defined in terms of a single sphere, its neighboring pore space and the ice bonds (necks) where the sphere contacts other spheres. When regular uniform packing is assumed, every sphere will, theoretically, contact Ν other spheres. In the case of the idealized snow considered here, the coordination number, N, will depend on the type of packing and the ice-volume fraction, ϕ i, i.e. the volume occupied by the ice for a given volume of snow. In the case of a dry snow cover this may be represented by ϕ i = ρs/ρi, where ρs and ρi are the density of snow and ice respectively. An estimate of the coordination number used in this paper is
The number of cells, nc (which is the same as the number of spheres) in a sample volume is simply calculated by

The number of cells in the length of a sample cube, ncl , is the cube root of nc and the average number of cells in the cross sectional area of the sample cube, ncA , is the square of n cl. Dimensions of this cube should be much greater than the dimensions of the individual cell.
Heat Transfer in Snow
For composite systems it is useful to consider, by analogy to Newton’s law for cooling, an overall heat-transfer coefficient U, defined by
A discrete form of Fourier’s law for two temperatures separated by a distance l may be written as
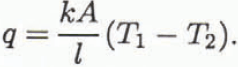
Thermal resistance is defined as

so that

(e.g. Incropera and de Witt, Reference Incropera and deWitt1981).
In this analysis the series and parallel paths for heat flow are envisioned as in Figure 1. A configuration such as this would in fact be two-dimensional, but for the development presented a one-dimensional assumption is felt to be satisfactory.
In the case of snow the components of the total thermal resistance, R t, in the direction of one-dimensional heat flow is considered to be due to the necks, R n; to the ice grain and pore in series, R ip; and to the pore, R p. Then


Fig. 1. The effective thermal conductivity is examined by considering a partitioned cube. All of the heat flow is assumed to be one dimensional. Ap, Ac and Aip represent, respectively, the projected areas of the pore, contacts and icelpore in series in the direction normal to the temperature gradient. Lengths of the ice, li, and pore, lp, in series are calculated based on their respective cenlroidal distances from the axis of the sphere in the direction of heat flow; therefore, although not apparent from the figure, in general their sum will be greater than l.
Heat flow through the ice network is usually considered to predominate, due to the higher thermal conductivity of ice, k i, relative to the moist air. Consequently, thermal resistance due to the necks is developed first. In the case of constant heat flux, the thermal resistance of a circular contact area of radius, rc , on a semi-infinite sphere is given (Reference Carslaw and JaegerCarslaw and Jaeger, 1980) by
In regular uniform packing there are N/3 contacts for each sphere in each of three orthogonal axis directions; therefore there are N/6 contacts for each of the two opposite directions along an axis in the direction of the temperature gradient. For example, in simple cubic packing each sphere contacts six other spheres with one contact on the top and one on the bottom of the sphere. Reference KaganerKaganer (1966) shows the heat flux of one sphere by conduction through the contacts to be

where R sphere is the thermal resistance of a sphere with two contact areas aligned in the direction of heat flow. To an accuracy considered sufficient for this development, Kaganer demonstrates that Sphere R sphere ≈ 2R ∞. Using this in conjunction with Equations (7) and (8) for the ice spheres yields

Next, the ice and pore taken in series is addressed. Using Equation (4) the contribution of the series may be written as

The lengths of the ice, li , and pore, 1ps , in series are calculated based on their respective centroid lengths measured relative to the axis of the sphere in the direction of heat flow; therefore, in general their sum will be greater than l. This causes some confusion in the visualization rendered in Figure 1, but it is not an analytic difficulty. A ip is the projected interface area between the ice and pore in series in the direction of the temperature gradient. k ap is the apparent conductivity in the void between the ice grains. Apparent conductivity is due to the conductivity of the pore and the conductivity due to vapor flux,
Conductivity due to the vapor flux is

L v is the latent heat of vaporization of water, R the gas constant of water, D is the diffusion coefficient of water vapor in air, Ρ total pressure and P wvs, the saturated water-vapor pressure (Reference LunardiniLunardini, 1981).
Finally, by Equation (4), the contribution due to conduction through the pore alone is simply given by

Combining Equations (9), (10), (13) and (6), an effective thermal conductivity for a sample based on a unit cube (eg. one meter) is written as

Results
Computation of the effective thermal conductivity for the idealized snow cover as developed above is examined for several cases. In Figures 2–6 the effective thermal conductivity (14) for the snow cover and the contributions of the various “paths” of heat transfer as calculated in each of the terms on the righthand side of Equation (14) are presented.

Fig. 2. The temperature dependence of the effective thermal conductivity of snow at a density of 300 kg m−3 and a ratio of the contact radius to the grain radius, rc/rs, of 0.2 as calculated. The individual contribution of the conductivity due to the different paths of heat transfer are also represented.

Fig. 3. The temperature dependence of the effective thermal conductivity of snow at a density of 300 kg m−3 and rc/rs of 0.01 as calculated, as are the component contributions which combine to form the total.

Fig. 4. Density dependence of the effective thermal conductivity of snow at a temperature of −5°C and rc/ra of 0.2.

Fig. 5. Density dependence of the effective thermal conductivity of snow at a temperature of −5°C and rc/rs of 0.01.

Fig. 6. Dependence of the effective thermal conductivity of snow on rc/rs, at a temperature of −5°C and a snow density, ρB, of 300 kg m−3.
Figures 2 and 3 depict the conductivity as a function of temperature. Both figures represent a snow cover of 300 kg m−3 density, but in Figure 2 the ratio of contact (i.e. neck) radius to ice-grain sphere radius, r c/r s, is 0.2 and for Figure 3 it is 0.01. Notice that for the larger ratio the major contribution to the effective conductivity is due to the ice network which is interconnected through the contacts or bonds (9). When the area of the contact between ice-grain spheres is very small (Fig. 3) the contribution of the ice and pore in series (10), which accounts for the vapor flux (12), becomes the dominant component. At the warmer temperatures this in fact results in the effective conductivity increasing with increasing temperature. It should be noted however that effective conductivity is in general much greater for the well-bonded snow.
The influence of temperature on the effective thermal conductivity of snow has not been extensively investigated. However, Reference Voitkovskiy, Golubev, Lapteva, Troshkina, Ushakova and PavlovVoitovsky and others (1974) showed the thermal conductivity increasing with a concave upward slope for temperatures above 248K and Reference Pitman and ZuckermanPitman and Zuckerman (1967) indicated a general increase in conductivity based on measurements taken at three temperatures: −88°, −27° and −5°C.
Figures 4 and 5 address the influence of snow density for a fixed temperature of −5°C and r c/r s of 0.2 and 0.01, respectively, as in Figures 2 and 3. The sphere contact dimensions influence both the components and the overall effective conductivity in a similar pattern to the temperature-dependence case above. In addition, for the case of the extremely small contact-to-grain ratio the conduction through the ice network in the lower-density snow is actually calculated to be of less significance than the pure conduction in the pore.
The ratio of the contact radius to the radius of the ice-grain sphere, r c/r s, is of obvious importance in this analysis. Its influence on the conductivity is examined at a constant density and temperature in Figure 6. Effective conductivity monotonically increases as the ratio increases and is essentially paralleled by the increase of conductivity of the ice network which is at zero when the contact area is zero. Except for at very small contact areas, this is the dominant mechanism which determines the effective conductivity, and it varies significantly as the ratio changes. All of the results presented were calculated based on a 1 mm ice sphere, but it should be pointed out that the grain-size itself has little effect on the outcome. The importance of the interconnection of the ice network was verified in an experimental study by Reference Adams and BrownAdams and Brown (1982), where it was noted that the magnitude of the temperature gradient through weaker layers was relatively larger than through strongly bonded layers. This process may well be self-enhancing in the sense that snow of low conductivity will result in large temperature gradients which produce poorly bonded depth hoar of lower conductivity, resulting in larger temperature gradients, etc. Depth hoar consists of faceted, usually weakly bonded, ice crystals. It develops while on the ground as the result of temperature-gradient induced mass flux (Reference AkitayaAkitaya, 1974).
A great many investigators have examined the influence of snow density on its effective thermal conductivity (see Reference MellorMellor, 1977). There is considerable scatter apparent in the results, which is probably due in large part to the highly variable nature of snow. An empirical equation developed by Reference YenYen (1981) which is applicable over a wide density range has the form
where ρ s has units of Mg m−3.
Yen’s equation (15) is compared to the analysis described in this paper for values of r c/r s of 0.01, 0.1, 0.2 and 0.3 at a temperature of −5°C (Fig. 7). The agreement of the analytic model with the empirically based equation taken as a function of density, particularly at the 0.2 ratio, is encouraging and lends credence to the approach. The strong variability of the effective thermal conductivity with respect to the relative bond size, however, emphasizes the importance of microstructure.

Fig. 7. Density dependence of the effective thermal conductivity of snow at a temperature of −5°C comparing the ratio of the contact radius to the grain radius, rc/rs at values of 0.01,0.1, 0.2 and 0.3 to the empirical fit for Yen (Reference Yen1981) for the effective thermal conductivity of snow as a function of snow density.
Conclusions
Results of the calculated effective thermal conductivity of the idealized snow do indeed show a strong dependence on snow density. However, the ratio of the neck radius to grain radius also plays a very significant role, and a variation with temperature is noted. A ratio of the neck radius to ice-sphere radius of 0.2, at a temperature of −5°C, yields a variation in which the effective thermal conductivity increases with density in a manner very similar to the empirical fit of Reference YenYen (1981).
The effective thermal conductivity of the snow decreases as r c/r s decreases. Conduction through the ice-bond network is the predominate mechanism of heat transfer, except at very low neck-to-sphere ratios. The relative contribution of the heat flow through the ice and pore in series increases slightly as this ratio decreases but increases with increasing snow density. The contribution of pure conduction through the pore is not shown to be important.
Based on the results from this analysis, as well as intuition and inference from other studies, it seems likely that microstructure plays a vital role in determining the thermal conductivity of a snow cover. Further research using physical models in which simplified snow micro-structure could be controlled and examined would be valuable for verifying and extending the work presented.
Acknowledgements
The authors would like to thank the Japanese Science and Technology Agency, National Research Institute for Earth Science and Disaster Prevention, Shinjo Branch of Snow and Ice Studies, for its support of this work in particular and, more generally, for the encouragement which it has demonstrated toward the advancement of international scientific cooperation.











