Introduction
Precise knowledge of the mass balance of ice sheets is essential for estimating their contribution to current and future sea-level rise. The numerous assumptions necessary to assess the global mass balance of Antarctica lead to significant discrepancies between the estimates (Reference Rignot, Velicogna, Van den Broeke, Monaghan and LenaertsRignot and others, 2011a; Reference Zwally and GiovinettoZwally and Giovinetto, 2011). The Ice Mass Blance Inter-comparison Exercise (IMBIE) consortium (Reference ShepherdShepherd and others, 2012) reconciled results from a range of different methods (input/output method (IOM), satellite altimetry and gravimetry) to determine that the average mass loss of the entire Antarctic ice sheet over the period 1992–2010 was 71 ± 53 Gt a−1. During this period, the East Antarctic ice sheet (EAIS) mass change may be positive (+14 ± 43 Gt a−1), while the West Antarctic ice sheet (WAIS) and Antarctic Peninsula ice sheet (APIS) lost mass (–65 ± 26 and –20 ± 14 Gt a−1, respectively). While the magnitude of change of the WAIS and APIS are therefore relatively well constrained, even the sign of the sea-level rise contribution from the EAIS remains uncertain.
A significant issue of mass change estimation is that none of the methods presently used are free from significant errors, and all rely on either models or approximations (Reference ShepherdShepherd and others, 2012). The IOM calculates the balance between the total surface mass balance (SMB) that feeds a given drain-age basin and the loss of ice through ice discharge at the basin outlet (e.g. Reference RignotRignot and others, 2008). Satellite gravimetry and altimetry (e.g. Reference GunterGunter and others, 2009) measure the absolute mass change but rely on a glacial isostatic adjustment (GIA) model, while altimetry also suffers uncertainty due to the densification process. As most of the drainage basins in the EAIS are close to equilibrium (Reference ShepherdShepherd and others, 2012), these methods struggle to provide good estimates, because a small error in the GIA model will introduce large relative errors in the results (Reference HannaHanna and others, 2013).
Nevertheless, a recent IOM study (Reference Zwally and GiovinettoZwally and Giovinetto, 2011) emphasizes that the IOM is equally prone to a large uncertainty. Indeed, the method is highly sensitive to the choice of the SMB as an input parameter. At present, several SMB datasets are available, either based on regional atmospheric modelling (Reference Van de Berg, Van den Broeke, Reijmer and Van MekjgaardVan de Berg and others, 2006; Reference Van WessemVan Wessem and others, 2014) or on data assimilation methods (Reference Arthern, Winebrenner and VaughanArthern and others, 2006). Reference Lenaerts, Van den Broeke, Van de Berg, Van Meijgaard and KuipersLenaerts and others (2012) compare several datasets and identify a discrepancy up to 15%, which is >300 Gt a−1 for the whole Antarctic ice sheet.
The IOM has another pitfall. When no thickness data are available, the flux gate is set seaward of the grounding line, with the ice thickness then derived from the ice surface elevation. This method assumes that the glacier reaches hydrostatic equilibrium a few kilometres beyond the grounding line and that ice thickness does not change significantly between the grounding line and the point where the ice shelf actually freely floats. However, these can be separated by several kilometres, so this assumption may not be correct. For instance, along the Princess Ragnhild Coast, East Antarctica, the grounding line and hydrostatic line are ~2 km apart (Reference BindschadlerBindschadler and others, 2011). Within this interval, under the Pine Island Ice Shelf, intense subglacial melting of up to several tens of metres per year can occur at the seaward side of the grounding line (Reference Payne, Holland, Shepherd, Rutt, Jenkins and JoughinPayne and others, 2007; Reference DutrieuxDutrieux and others, 2013) and may represent an important sink of mass which will affect the mass-balance estimation. This is one order of magnitude higher than the local SMB and will introduce a significant error into the mass-balance calculations. Moreover, any error in ice-shelf surface elevation is multiplied by a factor of ten when translated into ice thickness. An alternative to this approach is to calculate the outflow slightly upstream of the grounding line. Unfortunately, this can lead to two potential problems: (1) if radar measurements are not available, there is no remote-sensing method to estimate the thickness of the grounded ice and (2) ice dynamics must now be considered, since the independence of flow speed with depth (plug flow) is no longer valid.
Within the eastern Dronning Maud Land (DML) sector of the EAIS, only a limited number of glaciological studies have been carried out. Reference Van Autenboer and DecleirVan Autenboer and Decleir (1978) estimated the mass balance of the glaciers in the Sør Rondane Mountains (SRM), but their study was limited to the smaller glaciers within the mountain range, and does not include the primary ice flow outlets that flow through and are diverted around the major coastal mountain systems. On a continental scale, a number of studies have established the mass balance of DML drainage basins. The most recent such studies are those of Reference RignotRignot and others (2008) and Reference ShepherdShepherd and others (2012). Along the Princess Ragnhild Coast, Reference RignotRignot and others (2008) base their analysis on the flux through the ice shelf, where ice thickness is determined from hydrostatic equilibrium. Reference ShepherdShepherd and others (2012) assume the ice sheet in this area to be in equilibrium, since thickness data at the grounding line are lacking. In the meantime, GRACE (Gravity Recovery and Climate Experiment; gravimetry) and ICESat (Ice, Cloud and land Elevation Satellite; altimetry) reconstruction of the mass budget do not agree in eastern DML (Reference GunterGunter and others, 2009).
In this paper, we present the first estimate of the mass balance of the entire SRM glacial system using IOM. To avoid bias associated with the assumption of hydrostatic equilibrium, we base our calculations on data from an airborne radar survey which determined the ice thickness of the outlet gates slightly upstream of the grounding line. We then compare different datasets of SMB to investigate the impact of SMB uncertainties on the overall result.
Geographical Setting
The SRM glacial system consists of four large outlet glaciers which flow from the Dome Fuji ice divide toward the Princess Ragnhild Coast, DML (Fig. 1). West of the SRM are Tussebreen (TB) and HE Hansenbreen (HB; both between the Wohlthat Massif and the SRM). To the east, there are West Ragnhild Glacier (WRG; Reference Pattyn, de Brabander and HuyghePattyn and others, 2005; Reference Callens, Matsuoka, Steinhage, Smith, Witrant and PattynCallens and others, 2014) between SRM and the Belgica Mountains, and East Ragnhild Glacier (ERG) between the Belgica and Yamato Mountains. The position of these glaciers, and the surface flow speed (Reference Rignot, Mouginot and ScheuchlRignot and others, 2011b) are shown in Figure 1.

Fig. 1. Map of the Sør Rondane Mountains glacial system, Antarctica. Background colour shows the surface flow speed (Reference Rignot, Velicogna, Van den Broeke, Monaghan and LenaertsRignot and others, 2011a). Contours show surface elevations (Reference Bamber, Gomez-Dans and GriggsBamber and others, 2009). The four drainage basins are in purple. Their downstream section (grey curve) is the output gate used to determine the basin extension and the outflux. These are the gates surveyed by the radar and presented in Figure 2. Rock outcrops are shown in brown (SCAR, 2012). White curve is the grounding line (Reference BindschadlerBindschadler and others, 2011). SRM: Sør Rondane Mountains; WM: Wohlthat Massif; BM: Belgica Mountains; YM: Yamato Mountains; F: Dome Fuji. The glacier acronyms are TB: Tussebreen; HB: HE Hansenbreen; WRG: West Ragnhild Glacier; ERG: East Ragnhild Glacier. With exception of HE Hansenbreen, none of these glacier names are official, but a number of them have been frequently used in the literature (e.g. Reference Pattyn, de Brabander and HuyghePattyn and others, 2005).
Methods
Ice thickness measurements
To map the ice thickness at the grounding line, an airborne radio-echo sounding survey was carried out in the area during the 2010/11 austral summer (Reference Callens, Matsuoka, Steinhage, Smith, Witrant and PattynCallens and others, 2014). The survey consisted of a series of cross-flow profiles, of which one was taken close to the grounding line of each of the glaciers (Fig. 1), as well as a longitudinal profile along the flowline. The radar system employed a 150 MHz centre frequency (Reference NixdorfNixdorf and others, 1999; Reference Steinhage, Nixdorf, Meyer and MillerSteinhage and others, 2001). The system recorded at a rate of 20 Hz. For further signal-to-noise improvement, the data were stacked tenfold, resulting in a horizontal resolution of 80 ± 20 m.
Ice thickness was derived using a constant radio-wave propagation speed of 168 m μs−1. The uncertainty in the thickness estimation is approximately ±30 m (Reference Steinhage, Nixdorf, Meyer and MillerSteinhage and others, 1999). Surface elevation was obtained by laser altimetry from the aircraft, and bed elevation was subsequently derived by subtracting the ice thickness from the surface elevation. We applied the geoid height of 20 m above the EGM96 ellipsoid (Reference RappRapp, 1997) to derive the surface and bed elevations relative to sea level (these data are available on Pangaea, doi: 10/1594/PANGAEA.836299).
The cross-profile geometry and the ice flow speeds are displayed in Figure 2.
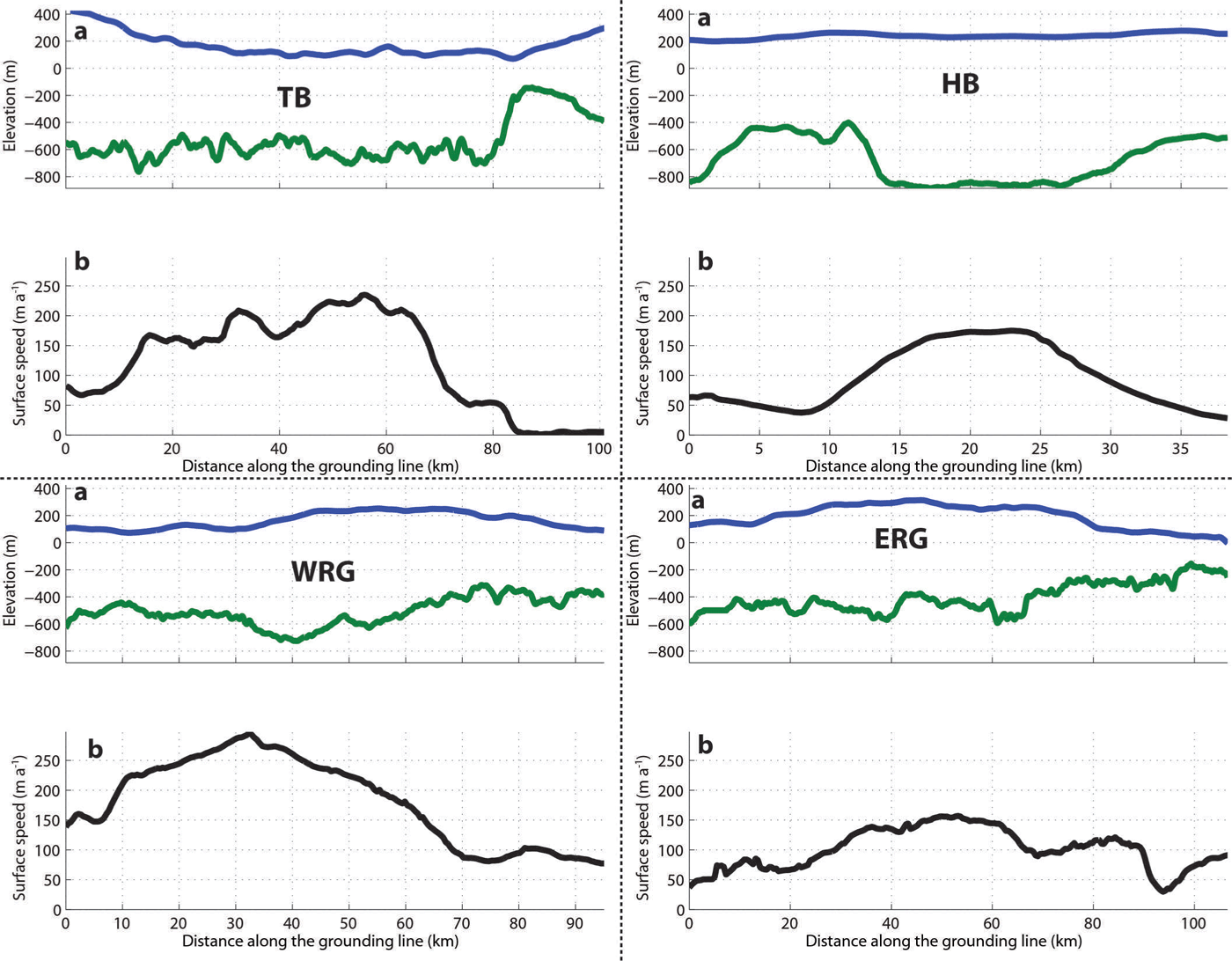
Fig. 2. (a) Geometry and (b) velocity profiles along the flux gate of each glacier, oriented west to east. The flux gates are chosen along the closest flight track to the grounding line. In (a) the blue curve is the surface elevation and the green curve is the bed elevation. In (b) the black curve is the surface speed (Reference Rignot, Velicogna, Van den Broeke, Monaghan and LenaertsRignot and others, 2011a). TB: Tussebreen; HB: HE Hansenbreen; WRG: West Ragnhild Glacier; ERG: East Ragnhild Glacier.
Surface mass balance
We determine the outlines of each drainage basin by backtracking flowlines from the outflux gate boundaries near the grounding line in the upstream direction. (The determination of the flux gates is given in the next subsection.) Starting from the grounding line, we trace flowlines on a surface digital elevation model (Reference Bamber, Gomez-Dans and GriggsBamber and others, 2009), until their convergence at the ice divide. We assumed that ice follows the steepest surface slope. A second step consists of integrating the SMB over each of the drainage basins. The SMB datasets used are those of Reference Van de Berg, Van den Broeke, Reijmer and Van MekjgaardVan de Berg and others (2006), Reference Arthern, Winebrenner and VaughanArthern and others (2006) and Reference Van WessemVan Wessem and others (2014); they are hereafter referred to as B06, A06 and W14 respectively. A06 is a dataset based on interpolation of ground-based observations (spanning 1950–2000), with a satellite-derived distribution. B06 is derived from the Regional Atmospheric Climate Model version 2 (RACMO2) at ~55 km spatial resolution, driven by the European Centre for Medium-Range Weather Forecasts’ ERA-40 reanalysis (1980–2004), and calibrated using ground-based measurements. W14 is also derived from RACMO2, on ~27 km spatial resolution, driven by ERA-Interim reanalysis (1979–2013), without any a posteriori output calibration. We assume that the mean SMB values over these periods represent these SMB models, and use them for the IOM calculations.
Outflow
The flux gates are defined along flight tracks of the airborne radar survey. The aim is to cover a maximum of the flux within the limitations of the radar survey (Fig. 2). However, as long as the basin is determined by the flux gate, all the ice flowing through the flux gate is supposed to have accumulated in the associated basin. Since we prescribe the gate width, no errors are associated with this quantity.
To estimate ice flux, we use the surface velocities of Reference Rignot, Mouginot and ScheuchlRignot and others (2011b), taken upstream of the grounding line and coinciding with the airborne radar profiles. The velocities are projected perpendicular to these flight lines, to account for the fact that the flowline is not exactly perpendicular to them: the norm of the velocity vector is multiplied by the cosine of the angle between the normal of the gate and the velocity vector.
When the flux gate is set seaward of the grounding line, it is common to assume that ice flow speed is independent of depth (plug flow) (Reference RignotRignot and others, 2008):
where Φ is the ice flux, U ⊥s(y) denotes the surface speed perpendicular to the flux gate (Reference Rignot, Mouginot and ScheuchlRignot and others, 2011b), H is the thickness, y the cross-flow direction and w and e denote the western and eastern boundaries of the gate. However, in this study, we set the flux gate on the grounded ice, where the ice flow speed can vary with depth, depending on the deformational characteristics. To assess mass-balance uncertainty associated with the flow regime, we consider different possible types of flow. First, we assume a plug-flow regime, Eqn (1), where the mean ice flow speed equals the surface flow speed. Second, we introduce a combined plug/simple-shear flow regime, in which the ice flow speed depends both on internal deformation and basal motion. For this purpose, we use the simplest way to describe ice flow according to simple shear, i.e. based on the shallow-ice approximation:
where Ū ⊥d is the depth-averaged deformational speed and τd(y) = –ρgH(y)|▽z s| is the driving stress. Other parameters in Eqn (2) are Ā and n, the depth-integrated temperature-dependent flow parameter and the exponent in Glen’s flow law, respectively. ε is the enhancement factor, ρ is the ice density, g is the gravitational acceleration and z s is the surface elevation. Following Reference Cuffey and PatersonCuffey and Paterson (2010), ε = 3, n = 3 and Ā = 3.5 × 10−25 Pa−3 s−1, so that Ā corresponds to a mean englacial temperature of – 10°C. Finally, the surface gradient, ∇zs, is derived from laser altimetry at the flowline, and we assume that it is constant along the grounding line cross section, so that ice thickness, H, is the only spatially varying parameter in Eqn (2). In order to reduce flow-coupling effects on short spatial scales, the surface gradients are calculated over approximately ten times the ice thickness (Reference Kamb and EchelmeyerKamb and Echelmeyer, 1986).
Once Ū ⊥d is determined, basal sliding, U ⊥ b, is taken as the difference between it and the observed surface velocity. For the shallow-ice approximation, this becomes (Reference Cuffey and PatersonCuffey and Paterson, 2010)
The total mass outflux at the grounding line is thus a combination of the flux driven by basal motion and the flux driven by internal deformation. This type of flow is hereafter called hybrid flow:
Error calculation
For the SMB datasets W14 and B06, the uncertainty in modelled SMB is derived from a comparison with 153 available SMB observations over the whole of northeastern DML (70–77° S, 0–65° E; Reference Van de Berg, Van den Broeke, Reijmer and Van MekjgaardVan de Berg and others, 2006). For each of the SMB observations, a comparison with modelled SMB is performed, and the total SMB uncertainty at each location is assumed to be the absolute difference between the two values. This uncertainty can be ascribed to both an uncertainty in observation and in the model. Uncertainties on observed SMB are assumed to be linearly proportional to the SMB itself (e.g. Reference RignotRignot and others, 2008). The remaining uncertainty, that which is ascribed to the model, is calculated as the square root of the difference between the quadratic total uncertainty and the quadratic observational uncertainty. The resulting 153 model mismatches are then averaged.
Since A06 is based on an interpolation of ground-based SMB measurements, this dataset is not independent of these measurements; in this case, we cannot assume that the A06 error constitutes an independent observational and model error. Therefore we assume a spatially homogeneous error of 10% over the entire basin (Reference Arthern, Winebrenner and VaughanArthern and others, 2006).
In order to calculate error on mass outflux, we only consider the error on the measured quantities: ice thickness, EH = ±30 m, and surface flow speed, E U s (Reference Rignot, Mouginot and ScheuchlRignot and others, 2011b). The error on the flux estimation under the assumption of plug flow is given by
For hybrid ice flow, error propagation leads to
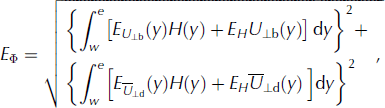
where
and
The error on mass balance is the quadratic mean of the error on input and output.
Results
Surface mass balance
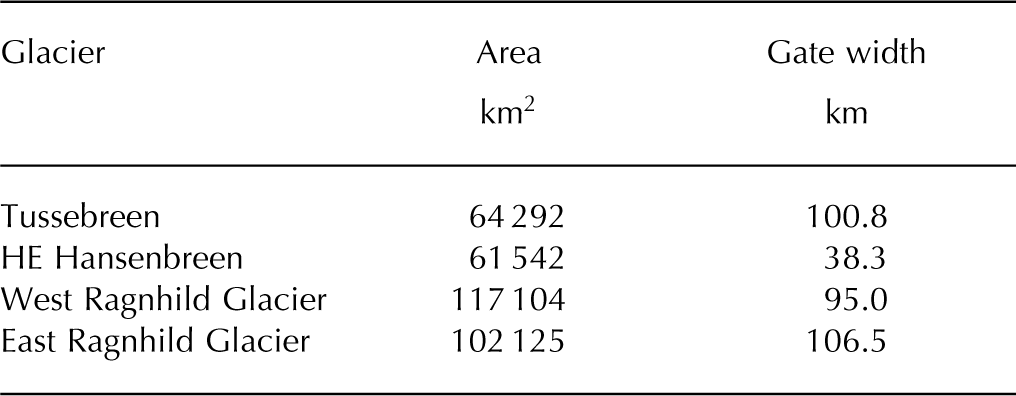
The backtracking of the flowline produces four large drainage basins, which extend from the grounding lines toward Dome Fuji ice divide (Fig. 1). Table 1 lists the characteristic sizes of each of the drainage basins.
Table 1. Basin extent and flux gate width for the adjacent drainage basins
The three mass input estimates are mutually consistent: they are bounded between 30.2 and 32.1 Gt a−1. Their spread is ~6% of the total SMB. Table 2 presents the errors in the estimation. These were calculated following the method described in the previous section and are based on the comparison between results of the model and 153 point measurements in DML. The specific surface mass balance is used in this calculation and is expressed in terms of SMB per area (mm w.e.m−2 a−1). For W14, the error in modelled SMB is 19.2 mm w.e. m−2 a−1, which corresponds to 26% of the mean of the observations (73.7 mm w.e. m−2 a−1). We assigned this relative error to the error on the area-integrated SMB. Therefore, the relative SMB uncertainty is ~26%, which we apply to the entire SRM glacial system and to the individual basins. The agreement of B06 with observations is similar. The error is 21.0 mm w.e. m−2 a−1, yielding a relative SMB uncertainty of 28%. Figure 3 shows RACMO2-based SMB datasets (B06 and W14) compared with observations. B06 tends to underestimate SMB at the locations of in situ measurements. The median of the difference between models and observations is – 14 mm w.e. m−2 a−1, whereas W14 does not mis-estimate, since its median is equal to – 2 mm w.e. m−2 a−1.
Table 2. Results of the mass budget (Gt a−1) using three different SMBs and two flow regimes. A06, B06 and W14 refer to data of Reference Arthern, Winebrenner and VaughanArthern and others (2006), Reference Van de Berg, Van den Broeke, Reijmer and Van MekjgaardVan de Berg and others (2006) and Reference Van WessemVan Wessem and others (2014), respectively
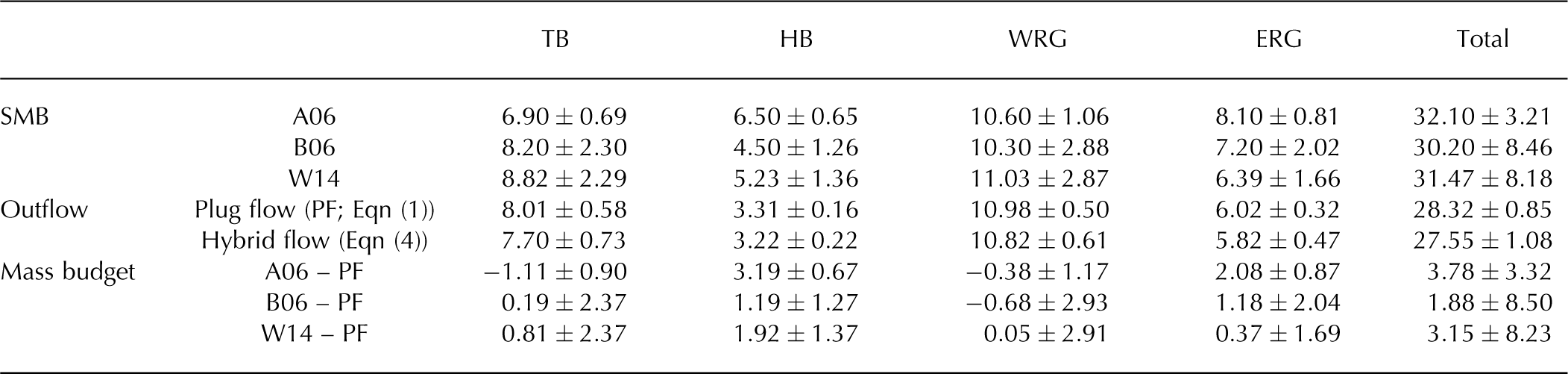
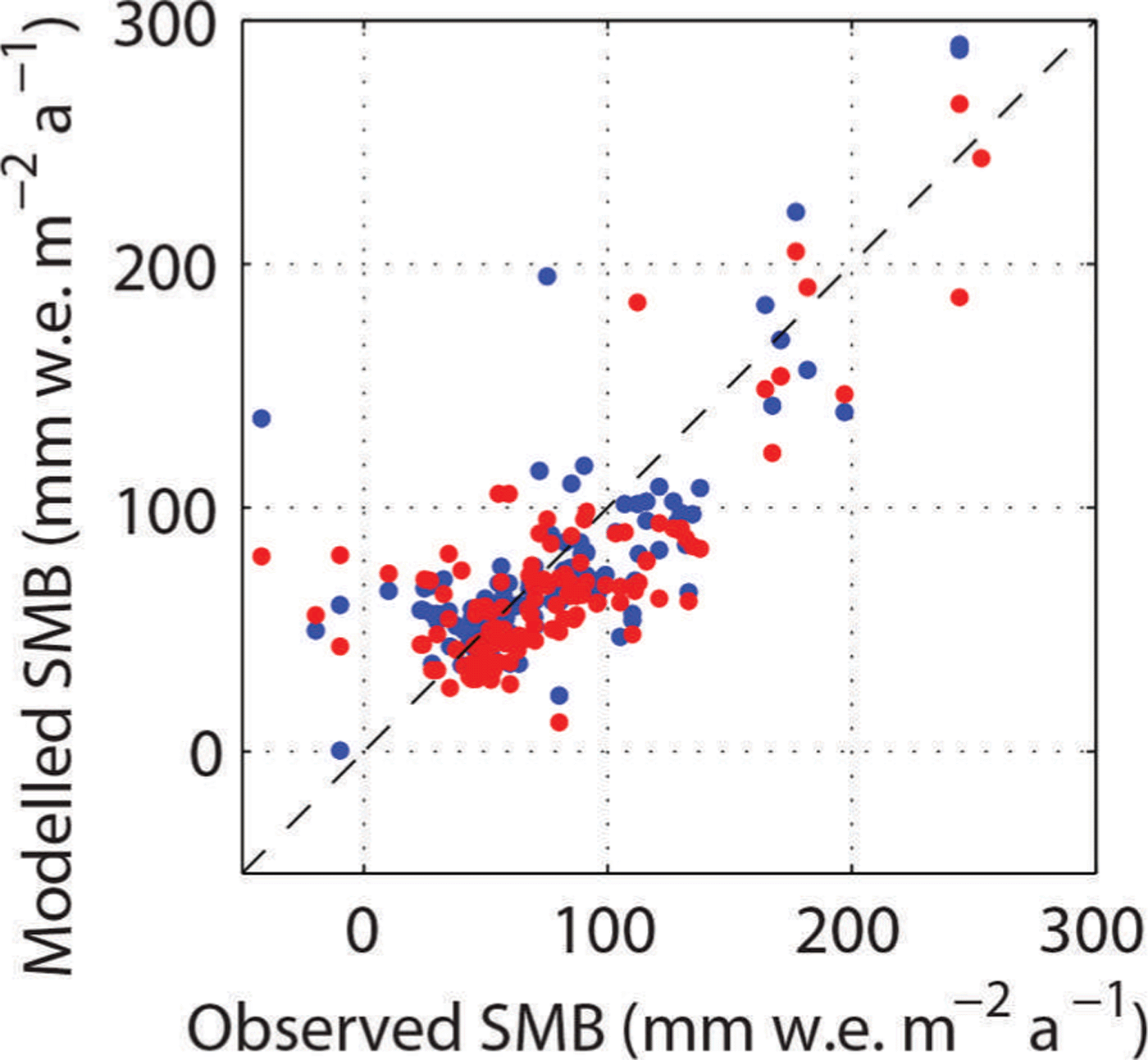
Fig. 3. Comparison of the in situ modelled SMB with observations, with W14 shown in blue and B06 in red. The dashed line is the identity line.
Errors are significantly higher for B06 and W14 than for A06, due to the different methodologies used to calculate the error. For B06 and W14, we compare the model to point measurements and evaluate the discrepancy. The uncertainty on A06 is set to 10%, as stated by Reference Arthern, Winebrenner and VaughanArthern and others (2006). However, their continent-wide error estimate does not necessarily reflect the local errors.
Outflow
Depending on the assumption made about ice dynamics (plug flow/simple shear), the total outflux varies from 27.55 to 28.32 Gt a−1. The errors were calculated using the method described in Eqns (5–8). They are significantly lower than uncertainties in SMB. At basin level, the mass outflux is a function of the width, the thickness and the flow speed (Eqns (1) and (4)). As revealed by the size of HB, the gate width is a first-order parameter in the calculation of the outflow. However, TB, WRG and ERG have the same width, but the outflow from the latter is 55% of the amount drained by WRG. This large discrepancy is due to the much higher ice flow speed across the grounding line of WRG (and, to a lesser extent, of TB). Ice flow speeds of WRG and TB are up to 298 and 245 m a−1, respectively, while the flow speed of ERG is <152 m a−1.
Concerning the comparison between plug and hybrid flow, the differences remain very small and, in all cases, less than the uncertainties. Therefore, in the mass-balance calculation we will neglect the hybrid flow part and continue by considering only plug flow, because plug flow is the most likely flow type near grounding lines. The low value of ∇z s (ranging from 11:3 × 10−3 to 18:4 × 10−3) and the relatively small thicknesses lead to low flux due to internal deformation. Indeed, flux due to ice deformation (second term of Eqn (4)) is always one order of magnitude smaller than flux due to basal motion (first term of Eqn (4)). For instance, the former is equal to 0.65 Gt a−1 while the latter is 10.17 Gt a−1 in the case of WRG.
Mass balance
From the difference between the mass gain through the integrated SMB and the mass loss through the gates, we find that the glacial system is gaining mass slightly, i.e. 1.88–3.78 Gt a−1, depending on the SMB dataset used.
Discussion
The IOM shows consistently large errors for the three SMB datasets used. All datasets give a consistent signal in terms of mass. In general, A06 gives a higher total SMB compared with the datasets based on modelling, but overall results are comparable. B06 and W14 have the same orders of uncertainty, while A06 has a significantly lower error. This is due to the methodology used to ascribe errors to the SMB estimate. We cannot compare A06 with data, since it is an interpolation of them, so we have to rely on the error estimate provided by Reference Arthern, Winebrenner and VaughanArthern and others (2006): maximum 10%. Nevertheless, the errors on SMB represent the majority of the uncertainty for each scenario.
Smallest errors are found on the outflow, as expected: the size of each basin consistently depends on the size of the outflow gate, which has been well defined from the airborne radar data along the grounding line. For the mass outflow, the assumption of plug flow compared with the hybrid approach seems acceptable. The difference between plug flow and hybrid flow is never larger than the calculated uncertainty (Table 2). As shown by Reference Callens, Matsuoka, Steinhage, Smith, Witrant and PattynCallens and others (2014), ice flow in the downstream section of WRG is primarily governed by basal sliding, so that plug flow is an adequate approximation, which is also true upstream of the grounding line. This statement seems acceptable for the other glaciers, since basal motion dominates the flux. Although the shallow-ice approximation is not intrinsically valid for ice streams, it gives an endmember estimate of how far the results can be from the plug-flow assumption. The comparison supports the use of the assumption. The difference between plug and hybrid flow is never >5%, which is of the order of the magnitude of the error. Indeed, the relatively low surface gradient, ▽z s, implies a small driving stress, even if the ice is thick, hence it does not influence deformational ice flow. Therefore, the plug-flow assumption can be safely applied here.
Reference ShepherdShepherd and others (2012) show that the increasing mass balance observed in this area with GRACE between 2009 and 2011 is driven by a positive accumulation anomaly. However, their study assumed that the basins around SRM are in equilibrium, because of the lack of data to the contrary. Here we estimate mass balance for the mean SMB over the past 34 years (Reference Arthern, Winebrenner and VaughanArthern and others, 2006; Reference Van de Berg, Van den Broeke, Reijmer and Van MekjgaardVan de Berg and others, 2006; Reference Van WessemVan Wessem and others, 2014) and outflow based on surface velocities between 2007 and 2009 (Reference Rignot, Mouginot and ScheuchlRignot and others, 2011b) and a radar survey made in 2011. Based on these data, the SRM glacial system is slightly gaining mass. Given the mass budget of the EAIS estimated by Reference ShepherdShepherd and others (2012) (+14 Gt a−1) and the fact that they assumed equilibrium for the SRM glacial system, our new estimate of its mass budget, ranging from +1.88 to 3.78 Gt a−1, increases the continental mass budget by 13–27%, depending on the SMB dataset used. Unfortunately, the large errors due to the SMB uncertainties mean we cannot irrevocably conclude that SRM glacial system mass balance is positive.
Conclusions
Based on an airborne radar survey along and across the major outlet glaciers of the SRM glacial system, groundingline ice thickness has been accurately mapped for the major outlet glaciers. We calculated the mass output of the four drainage basins constituted by these glaciers. The outflow was then compared with the mass input from three different SMB datasets, in order to assess their mass balance.
This study gives new insights into the mass balance in DML by contradicting the assumption of equilibrium previously made. According to the latest model and thickness measurements near the grounding line, this part of Antarctica gains 3.15 Gt ice a–1. However, given the relatively large uncertainties and discrepancies in the SMB, this value needs to be treated with caution.
Acknowledgements
D.C. is funded through a FNRS–FRIA fellowship (Fonds de la Recherche Scientifique) and received an Yggdrasil mobility grant (Research Council of Norway). The radar survey was conducted by the Alfred Wegener Institute, Germany, with further logistical support from the Princess Elisabeth station (Belgian Antarctic Research Expedition, BELARE), and was funded by the European Facilities for Airborne Research (EUFAR). We used the Quantarctica GIS package from the Norwegian Polar Institute (http://www.quantarctica.org/). We are indebted to M. Depoorter for help in improving the quality of this paper.







