Introduction
The problems of monitoring and predicting iceberg drift have long been of concern to maritime interests in the Arctic Ocean and adjacent areas, where their occurrence presents considerable hazards to drilling operations and shipping (Reference Bigg, Wadley and Stevens DPand JohnsonBigg and others, 1997). Recently, icebergs in the Southern Ocean have also begun to attract attention because of their sensitive responses to global warming (Reference Vaughan and DoakeVaughan and Doake, 1996) and possible usage as a source of fresh water for arid parts of the world. Hence, many models have been produced to provide detailed information on and forecasts of iceberg activities in the seas concerned (Reference Gladstone, Bigg and NichollsGladstone and others, 2001). Iceberg size distribution is one of the most important factors to be considered, because it not only presents the probability of encountering icebergs of different sizes in the area and but can also be closely associated with the calving process of the iceberg in its life cycle (Reference CrockerCrocker, 1993).
Marine radar is a powerful tool for detecting icebergs and even sea ice within a local area, and has been used widely in the polar regions and other ice-infested seas such as the Bohai Sea, China (Reference Xiao, Shao and ZhangXiao and others, 2006). Sea-ice observations using marine radar have some limitations in chaos instability induced by ship sway and wave undulation; however, nonlinear chaos theory established in the 1990s greatly improved sea-ice detection by marine radar (Reference LeungLeung, 1995). Moreover, current marine radar can detect bergy bits and growlers 1 m above the water and receive 3 dB signals (Reference O’ConnellO’Connell, 2008), so there is no problem with larger icebergs. Compared with observation by eye, the all-weather ability of radar can avoid the effects of night and bad weather.
In this study, icebergs in the Southern Ocean observed by ship-based marine radar during the 19th Chinese National Antarctic Research Expedition (CHINARE) are described. Iceberg sizes are extracted from these observations, and the characteristics of iceberg distribution in the three main sub-seas (the Weddell Sea, the Ross Sea and Prydz Bay) are discussed.
Field Observations
During the 19th CHINARE, the R/V Xuelong sailed around Antarctica from 64.38 S, 174.2°E to 69.28 S, 76.3° E from 17 December 2002 to 20 January 2003 (Fig. 1). Along the cruise track, most icebergs were observed in the north Ross Sea, north Weddell Sea and Prydz Bay.

Fig. 1. The cruise track of the 19th CHINARE in the Southern Ocean from 17 December 2002 to 20 January 2003, along with the iceberg drift vectors on the route. Circles denote the position of icebergs, and lines denote the velocity of iceberg drift.
The marine radar on the R/V Xuelong is Sperry Marine with a wavelength of 10 cm. The antenna fixed on the top of the cab is 30m above the water and can detect icebergs within a range of 45 km, particularly icebergs >2 km in length. Sea ice and ocean waves can also be detected by the marine radar, but very few ice floes were encountered during this summer cruise except for some first-year sea ice in Prydz Bay. Moreover, their effective height above sea level is significantly lower than the icebergs, so radar reflections from them are much weaker than from icebergs. Only floes and waves very close to the ship (4–8 km) can be detected by the marine radar. Compared with the large detection area of icebergs, such noise information within the small region can be ignored and easily excluded from further processing.
Marine radar images can be collected using a digital camera at certain time intervals. A typical radar image is shown in Figure 2. To obtain the size of an iceberg, certain coordinates need to be confirmed on the radar image: (1) the center of the radar image, namely point O, also the location of our ship, which is used for position checking between different images; (2) two points of intersection between equidistant cirques and the scanning beam on the radar image, namely R1 and R2, aiming to confirm pixel quantity of known distance on the radar image; (3) two vertexes on the long axis of an iceberg, namely B1 and B2. The actual size of an iceberg can then be calculated based on the known actual distance of R1R2. It is worth noting that iceberg length is always defined as the iceberg’s maximum dimension at the waterline, but the iceberg size calculated here (B1B2) is a little different from that definition and more like a measure of the maximum length of the iceberg perpendicular to the radar beam. Nevertheless, B1B2 is still an effective measure of the horizontal dimension of icebergs and a possible alternative to iceberg length from the point of view of statistics because the icebergs seem to distribute randomly around the ship (e.g. Fig. 2), although the orientation of icebergs is unknown.

Fig. 2. Iceberg observations by marine radar. O denotes the location of the ship, R1 and R2 are two intersections between equidistant cirques and the scanning beam, and B1 and B2 are two ends of an observed iceberg.
Iceberg Size
Iceberg size in different regions
Observed icebergs were concentrated mainly in the Ross Sea, Weddell Sea and Prydz Bay and were possibly calved from adjacent glaciers and then transported by the Antarctic Circumpolar Current. A total of 1085 icebergs was recorded with a minimum length of 68 m and a maximum length of 8169 m. Small icebergs <50m in length could not be detected because of the environmental noise received by the marine radar. The occurrence frequency of different iceberg lengths in each region is shown in Figure 3. A modal value of iceberg length in the range 800–1200 m is found from Figure 3. Super-large icebergs are rarely encountered in our observation because of the relatively low latitude of 60° S, so lengths of such icebergs distribute discretely in Figure 3. In addition, it is worth noting that a secondary peak appears in Figure 3b at ∼50m, which is thought to be a separate population created by calving from larger icebergs.

Fig. 3. Iceberg length histograms: (a) Ross Sea, (b) Weddell Sea, (c) Prydz Bay.
The statistics of all observed icebergs are summarized in Table 1, in which distance refers to the average distance between the icebergs and their most likely source in each region, namely the Ross Ice Shelf, the Larsen Ice Shelf and the Amery Ice Shelf for icebergs in the Ross Sea, Weddell Sea and Prydz Bay, respectively. It is interesting that both the shortest and longest icebergs are encountered in the Weddell Sea; moreover, this region contains >70% of all the observed icebergs. The emergence of numerous icebergs with distinct sizes in the Weddell Sea is strongly associated with the dramatic collapse of a large portion of the Larsen B ice shelf in March 2002, a short time before our investigation and which has thrown about 8 × 1011 m3 of ice into the Weddell Sea (Reference Shepherd, Wingham, Payne and SkvarcaShepherd and others, 2003; Reference DomackDomack and others, 2005).
Table 1. Statistical data of iceberg lengths

Curve fitting of iceberg size distribution
There are numerous observations for a fractal distribution of ice fragment sizes at very different scales (Reference TurcotteTurcotte, 1986; Reference Palmer and SandersonPalmer and Sanderson, 1991; Reference WeissWeiss, 2001; Reference Lu, Li, Zhang and DongLu and others, 2005), which actually implies the scale invariance of fracture and fragmentation patterns in ice. Fractal distribution is also used in analysis of iceberg size distribution and can be expressed in a form of power-law function as:
where N is the number of icebergs with size >L, N 0 is the total number of icebergs in the sampling area, D is the fractal dimension and C 0 is a non-dimensional parameter.
However, a deviation from the fractal distribution is also frequently reported in scaling analysis, especially for cumulative distributions of ice pieces in summer (Reference Lensu and MäättänenLensu, 1990; Reference Savage, Crocker, Sayed and CarrieresSavage and others, 2000). Generally, a finite size effect depending on the ratio of particle size to sampling area (Reference Rothrock and ThorndikeRothrock and Thorndike, 1984) and the thermodynamic effect on the ice-forming process are considered to be the two most important reasons for such deviation (Reference Lu, Li, Zhang and DongLu and others, 2008). In this case, the Weibull distribution is found to be a good alternative and can be expressed as
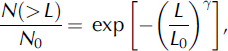
where 7(>0) is a shape coefficient and L0(>0) is a scale coefficient.
In addition to the aforementioned relationships, the Rayleigh distribution and inverse exponential distribution were also used in similar analyses (Reference NeshybaNeshyba, 1980; Reference CrockerCrocker, 1993), but both are specializations of the Weibull distribution and thus need no additional discussion.
Cumulative size-frequency of iceberg size data is fitted to the fractal distribution and Weibull distribution, respectively (Fig. 4). The results are summarized in Table 2, in which R1 is the correlation coefficient of Eqn (1) and R2 is the correlation coefficient of Eqn (2).

Fig. 4. Curve fits of iceberg length distribution to different functions: (a) Ross Sea, (b) Weddell Sea, (c) Prydz Bay. The solid line is for Weibull fits and the dashed line is for fractal fits.
Table 2. Results of curve fits (corresponding to Fig. 4)

From Figure 4 it is apparent that the fractal distribution gives a lower fit to the middle range of the data, but overestimates the measured data for both the smallest and largest sizes. In contrast, the Weibull distribution appears to give a better fit, with all the correlation coefficients exceeding 0.9 (Table 2). However, it is still worth noting from Figure 4 that with increasing iceberg length the Weibull distribution in the form of Eqn (2) also begins to underestimate the measured data, and plots of large iceberg lengths in the log-log coordinates seem to be much closer to a fractal distribution instead.
To validate this suspicion, a threshold value Lt is introduced into the curve fitting. Firstly, according to the relative errors of the Weibull distribution to the observed data, we define Lt as the iceberg length inducing a relative error of 20% for each region. Lt is then deduced to be 1250, 2200 and 2650m for the Ross Sea, the Weddell Sea and Prydz Bay, respectively. Subsequently, the Weibull distribution is still used for iceberg lengths <Lt and the fractal distribution is used for data >Lt. The results are shown in Figure 5 and summarized in Table 3.

Fig. 5. Curve fits of iceberg length when a threshold value Lt is considered: (a) Ross Sea, (b) Weddell Sea, (c) Prydz Bay. The solid line is for Weibull fits and the dashed line is for fractal fits.
Table 3. Results of curve fits using a threshold value L t (corresponding to Fig. 5)

An improved fit over the full range of the data is clearly seen in Figure 5 compared with Figure 4. Moreover, comparing Table 3 with the original fit in Table 2, we can see that the correlation coefficients are improved overall when the threshold value of iceberg size is considered, especially for the fractal distribution. However, the parameters of the Weibull distribution do not change as much because of the slight influence from the few discrete super-large icebergs. However, the parameters of the fractal distribution are obviously different from those in Table 2: in particular, C 0 in the new fit is many orders of magnitude greater than in the original fit, because the fractal distribution is now only fitted to super-large icebergs.
The existence of the threshold value indicates that the good correlation between the Weibull distribution and measured iceberg lengths is bounded towards the large scale by super-large icebergs. That is to say, the Weibull function is only suitable for the distribution of relatively small icebergs and the distribution of super-large icebergs is closer to the fractal function instead.
Given the different distribution model, the finite area effect depending on the ratio of particle size to sampling area as mentioned above is not important here because of our large investigation area (Reference Rothrock and ThorndikeRothrock and Thorndike, 1984), so such disagreement is thought to be due to the different thermodynamic effect on the forming processes of large and small icebergs (Reference Lu, Li, Zhang and DongLu and others, 2008). Most large icebergs are recently calved from an ice shelf and still in the primary stage of the life cycle, during which influences of thermodynamic actions (e.g. melting) are not so obvious for iceberg modification because of their large extents, so dynamic action by environmental forces is the primary factor controlling the calving process and subsequent modification. In contrast, small icebergs are mostly calved from a mother iceberg in the late stage of the life cycle, during which not only will the thermodynamic melting be sufficient to affect the calving process and modify iceberg shape, but also mechanical erosion (e.g. wave erosion at the waterline) will be enhanced in combination with melting to speed up the development of cracks (Reference CrockerCrocker, 1993), especially in the summer Southern Ocean near 608 S. As a result, the size distribution of large icebergs receiving fewer thermodynamic effects agrees well with the fractal distribution; conversely, the size distribution of small icebergs receiving more thermodynamic effects agrees well with the Weibull distribution.
Iceberg size in front of the Amery Ice Shelf
The Amery Ice Shelf is the source of icebergs in Prydz Bay, in which the R/V Xuelong sailed from 65.48 S to 68.2°S along the same longitudes 688 E during 13–15 January 2003. Within this area, icebergs mainly drift northward with a velocity of 0.30–1.87 ms−1 (Reference Lu, Cui, Liu, Bao and LuoLu, 2006). From analysis of iceberg size along the cruise track, variations of iceberg size in front of the ice shelf are presented in Figure 6. It is clear from Figure 6 that, as the ice shelf is approached, iceberg size first increases and then decreases, which is associated with the calving process of icebergs.
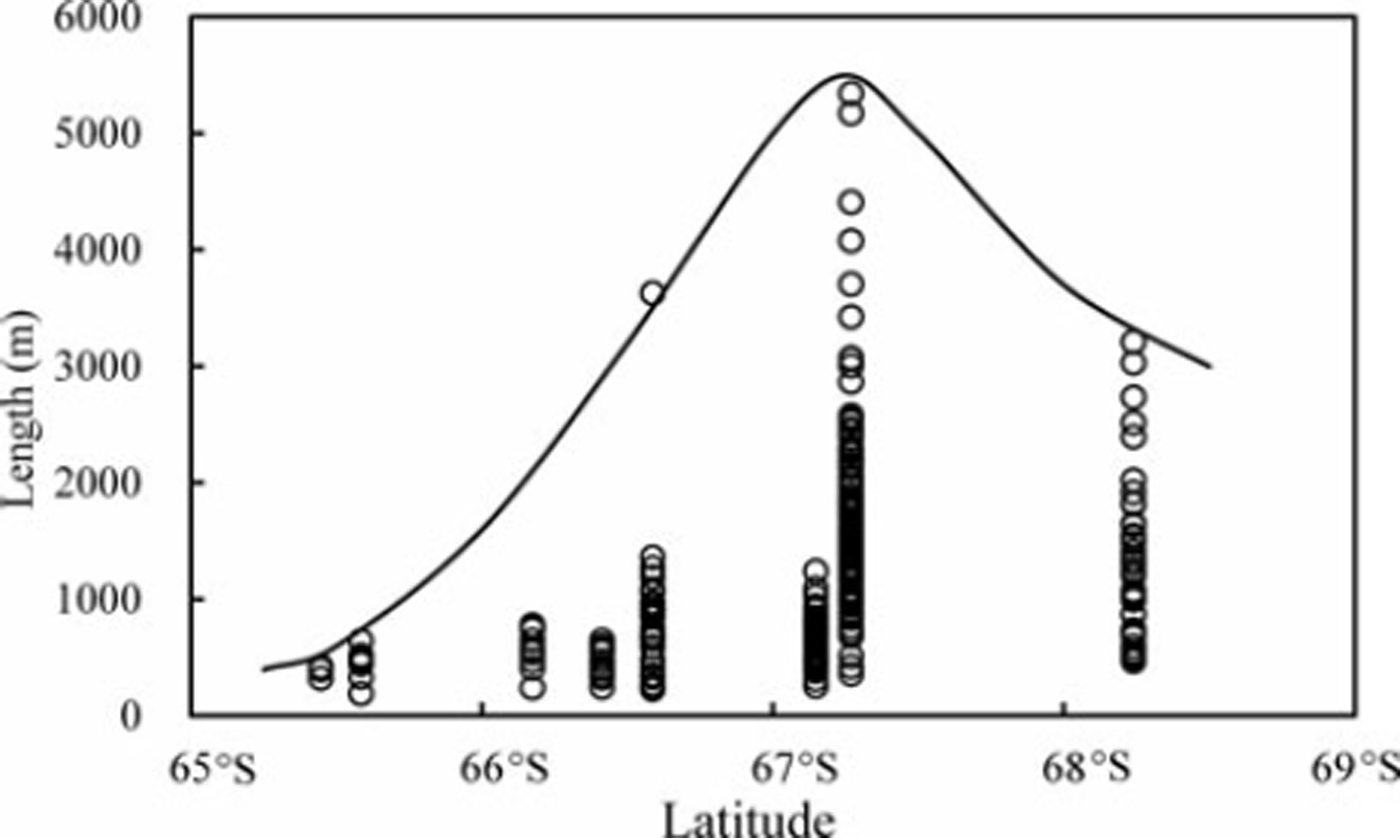
Fig. 6. Distribution of iceberg length over latitude on the route in Prydz Bay.
In the course of iceberg formation following ice-shelf collapse, isolated icebergs are not only produced along fractures of glaciers, but bergy bits and growlers calve from critical parts on icebergs because of static or dynamic loadings caused by sudden glacier calving. Hence there are always bergy bits and growlers around larger icebergs, while with the decreasing distance to the ice-shelf edge, iceberg size increases then decreases, as shown in Figure 6. These observations are in accord with the general mechanical rule of object collapse. However, with the exception of the peak at 67.38 S, icebergs near the ice shelf (68.38 S) are still larger overall than those far from the ice shelf (65.58 S), because icebergs close to the open ocean are more likely to disappear due to the increased influences from environmental dynamics and the melting process.
Conclusions
A total of 1085 icebergs in the Southern Ocean near 608S was observed by the marine radar on the R/V Xuelong during the 19th CHINARE from December 2002 to January 2003. The icebergs had a modal length of ∼1000m and 70% of them emerged in the Weddell Sea, possibly due to the dramatic collapse of a large portion of the Larsen B ice shelf in March 2002. Both the fractal distribution and Weibull distribution are applied to fits of cumulative probability of the iceberg lengths. It is found that the fractal distribution underestimates the measured data in the middle of the data, but overestimates them for both the smallest and largest sizes. The Weibull distribution shows a better correlation but also underestimates the measured data for large icebergs. Therefore a threshold value Lt is introduced into curve fitting and a better correlation is then obtained if the Weibull distribution is used only for iceberg length <Lt but the fractal distribution is used for data >Lt. This reveals that an upper limit exists in the good correlation between the Weibull distribution and the measured data, which is possibly due to different thermodynamic effects on the calving process and subsequent modification of large and small icebergs. The size of icebergs in Prydz Bay first increased and then decreased when approaching the Amery Ice Shelf, which is mainly attributed to the calving processes that occur after the icebergs separate from the ice shelf.
Although the definition of the threshold value L t is somewhat arbitrary in this study, the different distribution pattern of large and small icebergs is still obvious. Further studies will focus on determining the threshold value and the physical mechanism affecting the distribution patterns.
Acknowledgements
This research was supported by the National Natural Science Foundation of China (41276191 and 40930848). Z.L. carried out the field data collection from Chinese Polar Expeditions organized by the Chinese Arctic and Antarctic Administration. We thank all the crew on the R/V Xuelong for their help in using the marine radar on the ship.











