Introduction
An ultimate target of ice-sheet modelling is to incorporate and assimilate sufficient data to define the present state of the current ice sheets, in order to provide optimal forecasts (Reference Arthern and HindmarshArthern and Hindmarsh, 2003). Ideally, such a model would be able to represent all the appropriate non-linear dynamical features believed to be of importance: grounding-line motion, thermomechanical coupling and basal hydrology. Even this is ambitious, but more pertinent is the fact that, at the moment, the goal of linking together these processes with all the available data in one assimilation model is well beyond computational tractability. One response to this is to devise different models appropriate to different datasets. The example considered here is internal layers sounded by ice-penetrating radar. These are reflections induced by ionic variations in the ice, which arise from differences in the chemistry of the snow, and which are consequently interpreted as isochronal layers. It is the isochronal property that has allowed these layers to be increasingly incorporated as observations constraining ice-flow models (Reference Nereson, Raymond, Jacobel and WaddingtonNereson and others, 2000; Reference Nereson and RaymondNereson and Raymond, 2001; Reference Nereson and WaddingtonNereson and Waddington, 2002; Reference Siegert, Hindmarsh and HamiltonSiegert and others, 2003, Reference Siegert2004; Reference Martín, Hindmarsh and NavarroMartín and others, 2006; Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others, 2007). Simultaneously, associated theoretical advances in understanding how radar layer architecture is constructed are being made (Reference Hindmarsh, Leysinger Vieli, Raymond and GudmundssonHindmarsh and others, 2006; Reference Parrenin, Hindmarsh and RémyParrenin and others, 2006; Reference Leysinger Vieli, Hindmarsh and SiegertLeysinger Vieli and others, 2007; Reference Parrenin and HindmarshParrenin and Hindmarsh, 2007; Reference Martín, Hindmarsh and NavarroMartín and others, 2009), as well as consideration of the numerical techniques needed (Reference Rybak and HuybrechtsRybak and Huybrechts, 2003).
An example of the problem, taken from a study of Dyer Plateau, Antarctica (Reference WeertmanWeertman, 1993; Reference Raymond, Weertman, Thompson, Mosley-Thompson, Peel and MulvaneyRaymond and others, 1996) is shown in Figure 1. The basal topography is rugose; the layers are not seen throughout the depth of the ice, and the survey lines are of variable length and spacing, reflecting the difficulties in obtaining data. The aim is to construct a flow model which can predict the layer geometry on the assumption that the layers are isochrones, representing former surfaces of the ice sheet.

Fig. 1. Illustrating a typical problem. The example is Dyer Plateau (data digitized from Reference WeertmanWeertman, 1993). Surface topography is in light grey, basal topography in dark elevation-coded grey. The 20 survey lines are marked on the bed by thick dotted lines and on the ice surface by circles. For two of these survey lines the picked isochronic layers are shown; on these the ends are indicated with bars.
This paper outlines a finite-difference model which can be used to model the radar layers on the large scale. The method is not a fully coupled ice-sheet model, but includes steady-state models and time-dependent configurations where the change in thickness is prescribed, and where the thickness data are ideally obtained from other data or from different models. In practice, this is all that is necessary since: (1) areas from where the ice has retreated most probably did not provide source areas for present ice, and in consequence have not, in general, influenced the currently observable layer geometry and (2) in any case the thickness constraints obtained directly from data would most likely have been used to constrain any large-scale model incorporating grounding-line motion. Thus, the simplification is to assume a steady-state ice-sheet profile based on current data, or its time variation predicted by other models.
A difference between this method and a full mechanical solution is that the velocity shape functions (i.e. how the horizontal and vertical velocity vary with elevation, generally normalized by either the maximum value or the mean value) are specified. Frequently, the shape functions are chosen to be those which arise from using the shallow-ice approximation (SIA), perhaps accounting for thermal effects, but the choice is quite free, subject to the restriction that the vertical velocity shape function is computed from the horizontal velocity shape function using incompressibility and continuity, or vice versa.
The model is easily extendable to include temperature solutions, which are subject to the same set of caveats: the thickness field is prescribed through space and through time. Such an approach cannot be expected to provide realistic predictions of ice-stream evolution, but in the extensive regions where dissipative heating is small, thickness and accumulation-rate changes drive the basal temperature field, and the model can provide useful predictions which might be compared with radar data from the bed of ice sheets.
This paper outlines the finite-difference model, with emphasis on special formulae used to compute age near the base of the ice; and compares age and temperature fields against standard and extended analytical solutions. Finally, a problem that occurs when comparing models with generally undated isochrone data is to determine the age contour which best fits the layer. We present a formulation which is expressed in the language of control theory and can be used with the balance velocity model to invert for the controlling parameters (e.g. Mart´ín and others, 2006). The procedure is outlined and demonstrated.
Method
The method consists of
1. Computing the balance velocities. This includes the case where we can define how the ice thickness changes with time.
2. Choosing shape functions to describe the velocity. This might include plug flow, or Poiseuille flow with quadratics or higher-order polynomials, which arise from lubrication theory (SIA).
3. Applying these in a transformed set of advection– diffusion equations, finite-difference approximations to these equations are generated and solved. The governing equations can describe the motion of tracers, age contours or heat.
4. Where temperatures are solved and used to compute the shape function, we step back to (2) and iterate until a consistent set of shape functions is obtained.
5. The age solution is computed.
6. Computed age contours are compared with data.
The method requires upper-surface and basal topography, accumulation rate, prescribed rate of change of thickness, shape functions and either a prescribed geothermal heat flux (if temperature calculations are performed) or a prescribed basal melt rate.
Governing equations
Consider a Cartesian coordinate system, Oxyz(r, z), where r is a position vector of a point (x, y) with z pointing upwards. The mass-balance equation is given by where H is the thickness of ice, Q = (Qx ,Qy ) is the horizontal flux, a is the accumulation rate and m is the basal melt rate and all of these are functions of r and time, t , only. This equation requires a boundary condition for Q at inlets, but in most cases, since we consider a whole ice sheet, all boundaries are outlets. Throughout this paper, ice thickness, accumulation and melt rate are prescribed functions (often constant) of time. Under the assumption that flow is parallel to the surface slope vector, Equation (1) is used to compute the flux; when thickness is constant this quantity is the balance flux. Reference Budd and WarnerBudd and Warner (1996), Reference HindmarshHindmarsh (1997) and Reference Le Brocq, Payne and SiegertLe Brocq and others (2006) discuss the solution of this equation.
It is convenient to work in normalized coordinates, (r, ζ, t ) (where ζ is the ‘sigma’ coordinate), i.e.
where b(r, t ) is the height of the bed. Following Reference HindmarshHindmarsh (1999, Reference Hindmarsh, Straughan, Greve, Ehrentraut and Wang2001), the mapped tracer or ageing equation is
where X(r, ζ, t ) is the age of the ice, Q(r,t) is the flux of ice in the region 0 ≤ ζ ≤ 1, and the partial flux, q(r,ζ,t), is the flux of ice in the region 0 ≤ ζλ ≤ ζ. Note that by definition, Q(r,t) ≡ q(r,1,t). The operator, ∇H , represents the gradient in (x, y) along surfaces of constant ζ. The partial flux q(r, ζ, t) = α ζ 0 u ~r, ζ~ , t) dζ~. Under the assumptions listed above,
where ¯u(r,t) is the vertically averaged velocity. Examples of the shape function, υ, for the horizontal velocity are
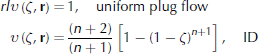
for plug flow and for isothermal internal deformation (ID) under the shallow-ice approximation. Under the same assumptions, the partial flux, ω, can be written in terms of the surface flux in the separable form, q = Qω(ζ,r), where ∂ω(ζ,r)/∂ζ = υ(ζ, r). For uniform plug flow (horizontal velocity independent of depth) and for uniform flow by internal deformation (ID) under the shallow-ice approximation, the flux shape function can be written as
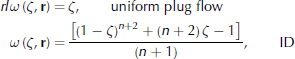
(Reference LliboutryLliboutry, 1979; Reference RaymondRaymond, 1983; Reference HindmarshHindmarsh, 1999). Here n is the index in the viscous relationship between the strain rate, e, and the deviator stress, τ :
More complicated forms arise when the rate factor, A, is a function of the height above the bed. Plug flow (which incorporates the case of sliding) and internal-deformation flow with a uniform rate factor are generally regarded as endmembers of the range of possibilities, at least where the bed is flat. Generally, non-isothermal flows lie between these two end-members.
To summarize, Equation (1) is used to compute the flux. The velocity distribution, in a form suitable for the age equation, can be deduced from the flux using Equations (4) and (5). These steps have eliminated the need to know the rate factor in the viscous relationship or sliding relationship. Given a geometry, the accumulation rate and a prescription of ω, all the information needed to solve the ageing equation (3) is present. This is also true for the temperature equation (7) below, which we now discuss.
Thermal effects can change the melt rate, m, and also the shape factors, υ, ω. With the balance velocities we can compute the temperature within the ice. Following Reference HindmarshHindmarsh (1999, Reference Hindmarsh, Straughan, Greve, Ehrentraut and Wang2001), the mapped temperature equation is
where k is the thermal conductivity of ice, c s is the specific heat capacity of ice, θ s is the prescribed surface temperature, G is the geothermal heat flux, ρ is the density and Tt is the basal tangential traction. This formulation positions all the frictional heating in a basal boundary layer, a procedure justified by Reference FowlerFowler (1992).
In words, the solution procedure is to start off with a zero melt rate and a velocity distribution corresponding to isothermal internal deformation. On the basal boundary the flux is set equal to the geothermal heat flux plus the dissipative heat flux. By including the dissipative heat flux here rather than distributing it through the column, we are appealing to the plug-flow asymptotics of Reference FowlerFowler (1992). This gives rise to a temperature field, and in the first iteration some points will be above melting point. Where this occurs, the basal boundary condition is reset to a prescribed temperature (pressure-melting point) and the temperature field is recomputed. Where the temperature field is thus prescribed, the melting rate is computed and the effect of this on the vertical velocity field accounted for, and the temperature field recomputed. This iteration proceeds until the temperature field stops changing.
Provided ω increases monotonically from the base, a further possibility is to solve the steady versions of the transport equations (3) and (7) in ω coordinates (Reference Hindmarsh, Leysinger Vieli, Raymond and GudmundssonHindmarsh and others, 2006; Reference Parrenin, Hindmarsh and RémyParrenin and others, 2006). This may be the best option in cases where one is focusing on the effects of horizontal variations in the shape factors, υ and ω. The age equation is

where subscript ω indicates that the vertical coordinate is ω rather than ζ; the divergence operator is taken along lines of constant ω. In cases where there is no slip at the bed, ωζ is zero and ∂Xω/∂ω becomes unbounded even for non-zero melting (physically, it is only Xω that is unbounded when the melting, m, is zero). This problem can be circumvented by using special finite-difference formulae, which are described in the next section.
The Finite-Difference Model
Finite-difference discretization
Here we outline the finite-difference model. As has been pointed out many times (two of the numerous examples in glaciology are Reference Hindmarsh and HutterHindmarsh and Hutter, 1988; Reference Greve, Wang and MüggeGreve and others, 2002), the advection equation presents special problems; in particular, one faces a trade-off between accuracy and physically realistic smoothness.
Equations (7) and (3) are discretized as follows, and are very similar to the formulae used by Reference Hindmarsh and HutterHindmarsh and Hutter (1988). The vertical diffusion operator is given by
with the same basal boundary formula as used by Reference Hindmarsh and HutterHindmarsh and Hutter (1988). Here ϕ can represent any field variable, while the notation Δ ζ represents the grid size in ζ, or more generally in the subscripted variable. The discretization of the vertical advection operator depends upon whether the temperature or advection equation is being solved. In the former case,
while in the latter case two-point upstreaming is used,
Two-point upstreaming can be used for horizontal advection,
while the first-order accurate one-point formula is less computer-intensive,
their accuracy relative to the two-point formula is compared in the next section. Similar formulae apply for y-direction gradients. The fluxes, Q, q and the derived quantity, ψ, are evaluated between gridpoints, so that their divergence is evaluated on the horizontal gridpoints. The equations are also solved at the gridpoints.
The age equation has high gradients near the bed and is singular for zero melting; we now derive special finite-difference formulae for the basal point. Firstly, for comparison, we note that in ζ coordinates, the regular finite-difference solution for the basal point (when melting is present) is
In ω coordinates, from Equations (10), the steady one-dimensional equation is
whence
where μ = m/ (a − m) . For isothermal flow by internal deformation, ω = [(1 − ζ)n +2 + (n + 2)ζ − 1/(n + 1), dω/dζ = 1− (1 − ζ)n +1 , so for small ζ
and we may write
Using this in Equation (12) we find that, near the bed,
so
and since for the lowest grid
we find
For plug flow, ω ≡ ζ, so dX = −dζ/(ζ+μ) , and our expression for the basal age is
The issue is now of the relative accuracy: how small does Δ
ζ
have to be before the formulae (13) and (14) are no longer better than the simple expression (11)? The ratios of the differences between X(0) and X (Δ
ζ
) computed from (13, ID special formula) and (14, plug-flow special formula) to the same quantity computed from (11, standard formula) are ![]() arctan
arctan ![]() and
and ![]() In
In ![]() , respectively.
, respectively.
These, of course, tend to 1 as ![]() tends to zero. Graphs of these functions are shown in Figure 2, showing that for the standard finite-difference formulae to be accurate, as indicated by a unit ratio, the discretization interval, Δ
ζ
, has to be somewhat less than μ (plug flow) or μ
1
/
2 (internal deformation). Given that μ is often ≤0.01, it is clear that the use of the special analytical difference formulae (13 and 14) is highly advantageous. Note also that the special formulae particularly increase accuracy for plug flow.
tends to zero. Graphs of these functions are shown in Figure 2, showing that for the standard finite-difference formulae to be accurate, as indicated by a unit ratio, the discretization interval, Δ
ζ
, has to be somewhat less than μ (plug flow) or μ
1
/
2 (internal deformation). Given that μ is often ≤0.01, it is clear that the use of the special analytical difference formulae (13 and 14) is highly advantageous. Note also that the special formulae particularly increase accuracy for plug flow.

Fig. 2. Illustrating the relative performance of special basal-point finite-difference formulae and standard finite-difference formula for the age equation. Vertical axis is the ratio of the differences in age between base point and point immediately above it of the special and standard formulae. Note that standard finite-difference formula overestimates the age considerably. Δ ζ is the grid size; μ is ratio of melting, m, to total mass balance, a − m. For plug flow the special formula is exact.
For ease of programming, one can write an effective shape function for the basal point given by
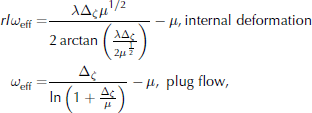
plug flow, which yields the analytical solution for the basal temperature when substituted for ω in the usual finite-difference formula (11).
If we are solving in ω coordinates, the equivalent expression (for the case of internal deformation) is
so we replace the expression ![]() using
using
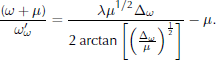
Obviously for plug flow the appropriate expression is Equation (15) since ω = ζ.
The main differences between the approach used here and that of Reference Hindmarsh and HutterHindmarsh and Hutter (1988) are (1) the rewriting of the advection operators in terms of horizontal partial flux gradients; (2) the optional use of horizontal first-order advection operators; (3) the special finite-difference formulae for the lowermost point; and (4) the optional use of the ω coordinate.
Solution of the linear equations
The finite-difference operators are assembled into a set of linear equations. We may conveniently write the solution in the form
where X is the age, AV and AH represent the discretized vertical and horizontal transport operators, and b is the righthand side resulting from the source term, δ, and the application of the boundary conditions.
This equation can be conveniently solved using Gaussian elimination for small problems, but for large-scale problems, such as solving for the age field in the Antarctic ice sheet, such direct methods are too demanding of computer memory, and iterative methods are used. One convenient method is to use preconditioned conjugate gradients, similar to that described by Reference Hindmarsh and HutterHindmarsh and Hutter (1988). The same ‘nested factorization’ preconditioner (Reference Appleyard and CheshireAppleyard and others, 1983) is used (see Appendix), but the bi-conjugate gradient solution method (Reference BarrettBarrett and others, 1994) is used rather than the Orthomin procedure.
An apparently attractive option is to solve the one-dimensional vertical transport equations (i.e. without the horizontal advection term) to obtain the temperature, which is not computer-intensive, compute the horizontal gradient of temperature and then to resolve the vertical transport equations with the horizontal advection as a source term. This iteration sequence may be written
A related possibility is to note that the linear equation (16) may be rewritten
where I is the identity matrix, which suggests an iteration sequence
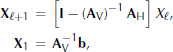
but it is easy to see that these two are equivalent in terms of stability, as both can be assessed by computing the eigenvalues of −(AV) − 1 AH . Practical experience and the computation of some numerical examples of the eigenvalue problem, with Fourier-space representations

where k is the wavenumber, j is ![]() and
and ![]() is the corresponding Fourier coefficient, suggest that this iteration is unstable for the age equation and the heat equation, though it is not clear that this is unconditional instability.
is the corresponding Fourier coefficient, suggest that this iteration is unstable for the age equation and the heat equation, though it is not clear that this is unconditional instability.
Analytical Solutions
Several analytical solutions for temperature and age are available, mostly related to one-dimensional vertical flow. These are extremely useful for assessing the accuracy of numerical solutions. Here we describe an extension to the well-known analytical solution for temperature due to Reference RobinRobin (1955), and briefly outline some two-dimensional solutions due to Reference Parrenin, Hindmarsh and RémyParrenin and others (2006) and Reference Parrenin and HindmarshParrenin and Hindmarsh (2007). A recent development which promises to be of great use in ice-sheet modelling is the thermomechanically coupled solution due to Reference Bueler, Brown and LingleBueler and others (2007); unfortunately this solution becomes singular in cases where the activation energy for ice creep is zero (i.e. the uncoupled case) and the balance velocity model used here could not be compared.
Extension of the Robin solution for one-dimensional temperature to include melting
The solutions here arise from the vertical-flow approximation. The steady-state diffusion advection equation for an ice sheet near its centre, where horizontal advection and dissipation can be neglected, is given by
where β = κ/H (a − m) , κ = k/ρc s, μ = m/(a−m), and for plug flow,
This relationship has a first integral
where superscript ‘b’ stands for evaluation at the base. We can thus write the formal solution In the thermally uncoupled case, W is simply a function of ζ and the computation of this solution is therefore just a quadrature, i.e. a numerical integration involving ζ only and not θ. The upper surface boundary condition can be inserted by evaluating the quadrature at the upper surface, ζ = 1, and eliminating θ b.
For plug flow we can readily obtain the solutions,
which is the extended Robin solution for μ l= 0 (see also Reference ZotikovZotikov, 1986, p. 89).
Figure 3 shows examples of analytical solutions compared with the finite-difference solutions for central areas of ice sheets, where horizontal advection is small. Clearly, close agreement is obtained for the temperature solution, while the age solution is quite good, apart from near the very bottom. Accuracy in this area is substantially improved by using the special finite-difference formulae.

Fig. 3. Comparison of finite-difference solutions (marked ‘FD’) with analytical solutions (marked ‘Ana’) for (a) temperature and (b) age. (b) also includes basal age computed using special finite-difference formulae (marked ‘FD*’). Special formulae can be seen to improve accuracy by at least an order of magnitude.
Solutions for the age equation due to Parrenin and co-workers
To test our age-equation solver when horizontal advection is significant, we compare it against analytical and semi-analytical results due to Reference Parrenin, Hindmarsh and RémyParrenin and others (2006) and Reference Parrenin and HindmarshParrenin and Hindmarsh (2007). Details of the solutions are given in these papers. They are obtained by transforming from physical space to a coordinate system of (logQ, log ω), in which the streamlines are straight lines. These are characteristics, and the age-equation solution is integrated along these.
Figures 4–6 show comparisons of the finite-difference solution with the solutions obtained by Parrenin and coworkers. The reader is referred to the papers given in the previous paragraph for details. Bedrock steps and lateral variations in the shape function (Raymond effect) are considered. Figure 4 shows a set of examples with horizontal advection represented by a first-order formula, while Figure 5 shows the same set of examples, with horizontal advection represented by a second-order formula. Both use the ζ-coordinate solution. The sharp bedrock steps result in breaks in slope of the isochrones, which are clearly captured by the characteristic solutions. The finite-difference solutions smooth these out, which, unsurprisingly, is particularly evident for the lower-order formula. Figure 6 considers a very sharp transition in flow mode from internal deformation (first and third sectors) to plug flow (middle sector), and also shows how use of the ω coordinate improves the solutions. In general, with the ζ coordinate, increased accuracy is obtained using the higher-order formula, but the use of higher-order methods can lead to deleterious features in the solution, particularly non-monotonicity. The ω-coordinate solution, with its superior ability to represent strong horizontal gradients in the streamlines, performs particularly well, so much so that there is no advantage gained in using the higher-order horizontal advection formula.

Fig. 4. Comparison of finite-difference solutions for age (colour-coded filled contours) with solutions obtained using the method of characteristics (white lines). Finite-difference solutions generated using first-order representation of the horizontal advection operator.

Fig. 5. Comparison of finite-difference solutions for age (colour-coded filled contours) with solutions obtained using the method of characteristics (white curves). Finite-difference solutions generated using second-order representation of the horizontal advection operator.

Fig. 6. Comparison of finite-difference solutions for age (colour-coded filled contours) with solutions obtained using the method of characteristics (white curves), for case with step jump in velocity shape function. The middle sector has plug flow, the outer sectors internal deformation. Finite-difference solutions generated using indicated order-of-accuracy representation of the horizontal advection operator, and use of ζ and ω coordinates are also indicated.
The Optimal Layer Fitting
Since radar layers are in general undated, we do not have any prior information about which particular isochrone should fit a given layer. Thus, there is an additional step in modelling radar layers, which consists of finding the modelled isochrone that best fits the observed isochrone. In essence, this is perfectly straightforward, but here we present a least-squares formulation, which can easily be extended to include optimal estimates of model parameters. This extended method was used by Reference Martín, Hindmarsh and NavarroMartín and others (2006), where the objective function for the flow model was given, but discussion of the method of finding the best isochrone was omitted.
Note that in this section m and n are different from the quantities used in previous sections. The ageing/tracer equation generates age solutions and, for example, streamline solutions Θ j , where j ∈ (1, f ) is an index counting the different observables, and Θ(r, ζ) represents a concatenation of all the observable fields. We deal with a discretized field of Θ, which is defined at a number of points in the horizontal as nh = nxny , and in the vertical nz , where nx and ny are the number of points in the x and y directions, respectively. For simplicity, we represent the picking and gridpoints as being coincident, but in general, and always in three dimensions, fitting is done by horizontal interpolation of the computed fields onto the picking points. The total number of points where the isochrones are fitted is nj = nhlj , where lj is the number of physical observables (e.g. layers or trajectories) and where f is the number of fields being solved for. It is straightforward to account for missing data points. The total number of solution points is m = fnhnz , and we let n represent the concatenation of the nj .
For each field we wish to find optimal fits to lj
elevation observations of radar data at a number of points with coordinates ![]()
with best-choice function for the modelled isocontours
Here there are lj
vector functions, ![]() represents the best model iso-estimate of the observable which fits the data and Θ
j
is the modelled field.
represents the best model iso-estimate of the observable which fits the data and Θ
j
is the modelled field.
Now we define Ô; Z(r) is a vector representing the concatenation of the vectors of all ![]() , Z(r) is a vector representing the comprising the concatenation of the vectors of
, Z(r) is a vector representing the comprising the concatenation of the vectors of ![]() with ζ comprising the concatenation of
with ζ comprising the concatenation of ![]() and lj
is the concatenation of all lj
. We seek to minimize
and lj
is the concatenation of all lj
. We seek to minimize
by varying Ô, which is the age or streamline of a given observed layer or trajectory. The covariance matrix, C Z- 1, indicates the errors associated with our estimate of Z(r). This idea is useful if some survey lines are better defined than others; it is also important in more-complex applications where model parameters are being estimated and require a covariance estimate for the prior information.
The objective function reads,
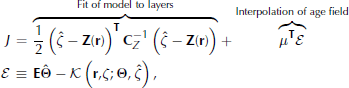
where
The vector μ is the Lagrange multiplier which enforces interpolation of the model field onto the layer. The function K(r, ζ;Θ, ζ) interpolates Θ at a given horizontal location onto the layer elevations, ζ, to yield while E is the corresponding constraint function and we have constructed E according to
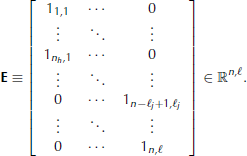
The gradient of the objective function is given by
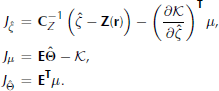
Here subscripts on J indicate partial differentiation with respect to the subscript, and
A turning point is found when all components of all these gradient vectors are zero. The Hessian of the objective function (which is also the Jacobian of the gradient system when applying Newton–Raphson iteration used to solve the system of equations) is given by
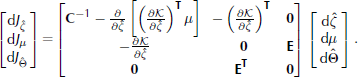
We shall construct K to be a linear operator on Θ, and we can then compute matrices K 0,K 1,K 2 such that
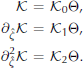
This is a fairly complicated way of stating a simple least-squares fit, but it has the advantage of being usable with more-complex control theoretic formulations which seek best estimates of flow parameters using radar layer information.
Where the flow model is perfect, fitting a best line is reasonably straightforward. More commonly, the flow model is wrong, and it can be wrong over different characteristic length scales, for example a length scale corresponding to unmodelled horizontal stress-gradient effects from rugose basal topography, or perhaps long-wavelength variations arising from a regional trend in the accumulation rate.
Both of these effects have particular consequences in three dimensions. The response of the isochrones to the topography depends upon the shorter of the two wavelengths (Reference Hindmarsh, Leysinger Vieli, Raymond and GudmundssonHindmarsh and others, 2006), which may be the one perpendicular to the radargram. When large-scale mismatches exist, viewing only one radargram which comprises a correlated cluster will appear to have a systematic error. Figure 7 shows some comparisons between observed and computed isochrones from Dyer Plateau data obtained by Reference WeertmanWeertman (1993), using the two survey lines shown in Figure 1. Layer geometry is computed on the assumption of plug flow, uniform accumulation and negligible melting. Figure 7a shows some short-range mismatches. An assumption of plug flow in a model typically predicts isochrones to drape over the basal topography, but horizontal stress gradients induced by short-wavelength basal topography cause overriding of layers (Reference Hindmarsh, Leysinger Vieli, Raymond and GudmundssonHindmarsh and others, 2006). This is clearly shown in the trough between 3 and 5 km. Otherwise, the method has produced a promising overall fit, presumably because along this line accumulation is uniform. Figure 7b shows data for the other survey line from Figure 1. It is clear that in some of the layers in individual lines the layer mean misfit is non-zero, but it should be remembered that the optimal-fitting method ensures that the mean misfit for each layer is zero over all the survey lines.

Fig. 7. Illustrations of the optimal-fitting procedure for the two survey lines shown in Figure 1, which can be identified from the basal topography. Thick solid curves are bed and surface, thin solid curves are picked layers, dotted curves are model predictions. Vertical lines indicate intersection points of the two survey lines.
Conclusions
The aim of this paper has been to detail the design of a radar layer simulation tool, and to give some idea of how well the convenient, but not always accurate, finite-difference method performs, by comparing it with analytical solutions.
In the vertical, it is important to be able to represent the steep gradients in age near the bed of the glacier. This has led us to use second-order upwinded methods, together with specially developed semi-analytical formulae for the bed points. The possibilitF2ies of adopting a streamline-based coordinate system have been pointed out.
For horizontal advection, higher-order methods are generally more accurate, but can lead to highly undesirable non-monotone behaviour. The first-order method tends to give a smoothed picture. Under certain conditions, the streamline-based ω coordinate can be very much more accurate than regular coordinate systems.
Finally, we have discussed an optimization technique for comparing modelled and observed radar layers.
Appendix: Preconditioning Algorithm
The notation in this appendix is different from that in the main section. The matrix equation requiring solution is
where A is a square matrix and x and b are vectors; we seek a preconditioner matrix, M, such that M is a good approximation to A. One useful approximation is
which may be written as
Here, L and U are lower and upper triangular matrices, respectively, while D is a band matrix, such that products of D − 1 and a vector can be efficiently computed, and I is the identity matrix. A standard procedure is to write the sequence
and the conjugate gradient procedure also requires solution of the equation A T x = b, or
which gives the sequence

Since L and U are triangular matrices, these sequences permit solution by backward or forward substitution.
>The nested factorization considers each dimension separately, so that the horizontal transport can be written
and
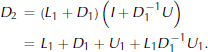
The matrix D 1 is a band matrix with sufficiently small bandwidth that the product of D− 1 1 with a vector can be computed easily by Gaussian elimination. In practice, it is the vertical transport operator plus elements from the horizontal advection operator that are located close to the diagonal. Used with the bi-conjugate gradient method, the linear equations can be solved to sufficient accuracy in five to ten iterations.



