Introduction
Around the coast of Antarctica and along the coasts of Arctic land masses, sea water freezes during the winter months into a continuous, visually featureless, floating ice sheet known as shore-fast ice. Ocean waves and swell that propagate towards the edge of the fast ice are partially reflected by the presence of the ice sheet. The transmitted energy causes bending which can lead to break-up of the ice sheet. In winter months the sheet may subsequently refreeze during calm periods, while in spring the ice eventually breaks up completely with currents carrying the ice floes away from the coast where they melt, leaving the coast free for the cycle to begin again the following winter.
Our focus here is on methods that have been used to calculate the reflection and transmission of ocean waves obliquely incident on the edge of fast ice. We make the usual assumption that the ice edge is straight over a distance that is long compared to the wavelength so that the approximation of an infinite straight ice edge holds. A mathematical model for treating the ice as a floating thin elastic plate is well known, and several studies have used this model to find reflection and transmission coefficients. Until recently only approximate or complex numerical methods for computing these values have been available. We review those methods as well as detailing methods of solution based on the Wiener-Hopf method, which, while following a complicated analysis, have recently been found to lead to very simple methods for computation.
The earliest method including the elastic response of the ice was given by Reference Hendrikson and WebbHendrikson and Webb (1963), and subsequently Reference Wadhams and UntersteinerWadhams (1986) who corrected minor errors in the earlier work. These authors used an incomplete set of modes and hence gave approximate solutions. Their method was to match travelling and damped travelling waves by satisfying continuity and boundary conditions on the surface at the edge of the ice cover. Subsequent comparison with exact solutions (Reference Fox and SquireFox and Squire, 1990) showed that these solutions correctly predicted the general trend for complete reflection at very short periods through to complete transmission at very long periods. However, these solutions contain erroneous features in the region of partial reflection and also do not conserve energy, the latter problem being extreme at short periods.
Reference Fox and SquireFox and Squire (1990) computed the reflection and transmission coefficients by solving the mathematical model exactly. They used the complete set of modes to express solutions with the coefficients found by matching through the water column beneath the edge of the ice sheet. The matching was performed numerically and led to a large system of equations that became unwieldy at short periods or large depths. Later this solution was extended to obliquely incident waves (Reference Fox and SquireFox and Squire, 1994) using the same basic method.
More than 30 years ago, Reference Evans and DaviesEvans and Davies (1968) formally solved the mathematical model using the Wiener-Hopf method. That method solves for the Fourier transform of the solution in each half-plane, i.e. over the region of open water and the ice-covered region. Until recently the solution given by Evans and Davies was thought to be unsuited for actual computation because the required inverse Fourier transform was too difficult. Indeed Evans and Davies stated this opinion in their report. That belief, coupled with the deceptively complicated calculations in the Wiener-Hopf analysis, caused this solution to be overlooked for many years. Two routes for taking that analysis through to stable computation have recently been found. In 1999 Reference Balmforth and CrasterBalmforth and Graster (1999) showed how the Wiener-Hopf analysis for a range of ice-sheet models could be made more straightforward by a formal application of the method with inverse transforms calculated by stable quadrature. We will outline a second route developed by the present authors in which the factorizations required in the Wiener-Hopf solution are written explicitly in terms of the wavenumbers of modes, and solutions are calculated as stable sums over these modes. Our advance over Evans and Davies is largely through a few modifications to the formulas and being able to find the roots of the dispersion equations. Furthermore, this method has a simple extension to the deep-water case by using the asymptotic behaviour of the coefficients to evaluate the expansion over the evanescent modes via an integration over the imaginary axis. The final formula for the solution consists of polynomials of the five roots of a fifth-order polynomial, with the calculation of reflection and transmission being very simple.
The deep-water problem has also been studied by Reference Gol’dshtein and MarchenkoGol’dshtein and Marchenko (1989), also using a Wiener-Hopf technique. They analyzed the asymptotic case when the rigidity of the ice tends to zero, concluding that the reflection becomes zero in that limit. Extension of the same method was used by Reference MarchenkoMarchenko (1997) to solve for wave propagation near a transition between different thicknesses of ice covers. Again, no explicit formula for the solution was given.
Mathematical Formulation
The elastic response of sea ice is modeled by treating it as a semi-infinite elastic thin plate. The effective rigidity of the ice sheet, l, is related to local mechanical properties by l = eh3/12(1 - v2), where e, h, and v are Young’s modulus, thickness of ice sheet and Poisson ratio, respectively. Consider an ocean wave of radian frequency ![]() arriving at angle ^at the edge of a semi-infinite ice sheet of thickness h floating on water of depth
arriving at angle ^at the edge of a semi-infinite ice sheet of thickness h floating on water of depth ![]() . This situation is depicted in Figure 1.
. This situation is depicted in Figure 1.
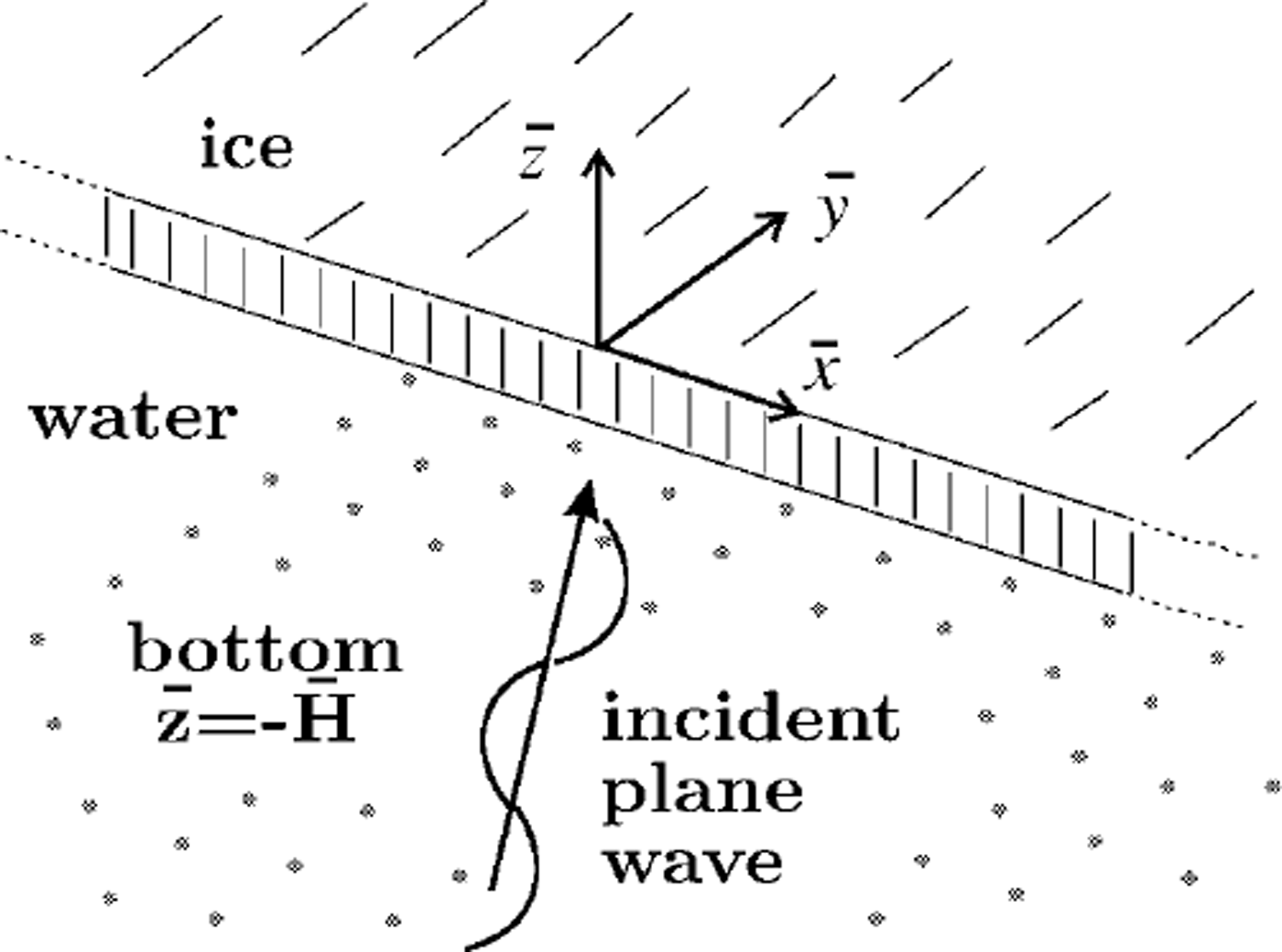
Fig. 1. Schematic drawing of plane ocean wave obliquely incident on a sea-ice sheet of thickness, h. the coordinate system used in the model is located on the edge of the ice sheet, and the sea floor is on ![]() .
.
The physical system is then formulated as a system of partial differential equations. We non-dimensionalize space and time variables by scaling with respect to the characteristic length i and the characteristic time ![]() respectively. Hence we define non-dimensional variables
respectively. Hence we define non-dimensional variables ![]() and
and ![]() given the physical values indicated by an overbar. Other quantities such as the velocity potential
given the physical values indicated by an overbar. Other quantities such as the velocity potential ![]() , vertical displacement of the ice sheet
, vertical displacement of the ice sheet ![]() , force acting on the ice
, force acting on the ice ![]() , radian frequency
, radian frequency ![]() , and mass of ice sheet per unit area
, and mass of ice sheet per unit area ![]() , are non-dimensionalized as follows:
, are non-dimensionalized as follows:

where pi and p are density of ice and water.
Since the incident wave has a single frequency, the time dependence and × dependence of the system can be assumed to be exp i(ωt + kx). Hence, the velocity potential is expressed as φ(x, y, z, t) = φ(y, z) exp i (ωt + kx). For the wave periods of interest, sea water can be taken to be incompressible, and hence the velocity potential φ(x, y, z, t) in the water satisfies Laplace’s equation. Equivalently, φ(y,z) satisfies Helmholtz’s equation
At the sea floor, the vertical component of velocity must be zero, hence φz = 0 at z = −h. Using Bernoulli’s thin plate theory (Reference Shames and DymShames and Dym, 1991), we find that the velocity potential at the ice cover satisfies

while the velocity potential on the free surface satisfies
The natural boundary conditions at the edge of the ice sheet, corresponding to there being no constraints at the edge of the ice, can be found by the variational form (Reference Shames and DymShames and Dym, 1991) of Equation (3). The resulting two boundary conditions are
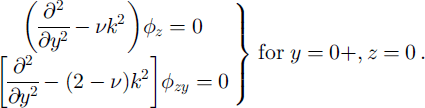
From these equations, the algebraic dispersion equations relating wavelength and frequency can be obtained. In the case of the free surface we have
Equation (6) has two real roots, ±λT, and an infinite number of imaginary roots, ![]() The dispersion equation for the ice-covered region follows from the plate equation (3), and is
The dispersion equation for the ice-covered region follows from the plate equation (3), and is
This dispersion equation for ice-coupled gravity waves has two real roots, ±μT, four complex roots, ![]() , and an infinite number of imaginary roots,
, and an infinite number of imaginary roots, ![]()
Methods of Solution
Any physical wave field, and in particular the solution we seek, can be expressed as a sum over the natural modes, or eigenfunctions, of the system. Since the eigenfunctions of Laplace’s equation with the boundary conditions given here have the form exp(iαy)cosh γ(z+ h), where γ 2 - α2 - k2 = 0, any bounded solution of the boundary value problem can be expressed as (Reference Fox and SquireFox and Squire, 1990)
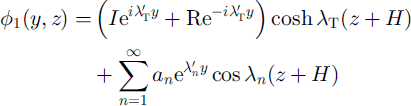
for y < 0, and

for y > 0. Here t, i, r, an, bn, b+
and b_ denote complex coefficients of various modes. Note that wavenumbers along the y axis are denoted by ![]() and
and ![]()
Simply put, solutions of the mathematical model are found by finding the coefficients in Equations (8) and (9), i, r, an, t, b± and bn. The different methods of solution correspond to different strategies for finding these coefficients.
Mode matching by Fox and Squire
Reference Fox and SquireFox and Squire (1990) obtained the coefficients for normally incident waves by minimizing the error function,

where α,β and δ are the positive Lagrange multipliers. Notice that on the righthand side of the equation the first and second terms enforce the continuity of the solution while the third term penalizes misfit in the natural boundary conditions. The minimum of the error function (which is zero) occurs for coefficients which give the solution, for any choice of the Lagrange multipliers. Fox and Squire performed the minimization by numerically solving the normal equations written in terms of the unknown coefficients. They often required many hundreds of modes to achieve the minimum with a reasonable precision. Reference Fox and SquireFox and Squire (1994) later extended this procedure to treat obliquely incident waves by treating the boundary conditions as "hard" constraints so the error function represented the misfit in continuity only. While this simplified the numerical procedure, it remains too unwieldy for general use.
Approximation by Wadhams
The method presented by Wadhams effectively assumed that the coefficients an, b± and bn, in the expansions (8) and (9), were zero, thereby omitting the evanescent modes in both water and ice sheet. As mentioned above, this method gives reflection and transmission coefficients that are correct in the simple regimes of extreme period and wavelength, but are in error for periods of geophysical significance (Reference Fox and SquireFox and Squire, 1990). In particular, this approximation does not predict characteristic features of the strain response near the edge of shore-fast sea ice. An example is the feature observed by Reference Squire, Rottier, Fox, Zhouwen, Tang, Preller and HuidingSquire and others (1994) during field measurements made in McMurdo Sound, Antarctica, which show that the surface strain of the ice is not a simple exponentially decaying function of distance from the edge of the ice sheet.
Unfortunately this solution continues to be referred to without recognition of its inaccuracies (Reference Wadhams, Parmiggiani, de Carolis, Tadross, Spezie and ManzellaWadhams and others, 1999), perhaps because of its mathematical simplicity.
Wiener-Hopf technique by Evans and Davies
The Wiener-Hopf technique (Reference NobleNoble, 1958) is applicable to a problem with a straight line boundary between semi-infinite domains. The method gives an algebraic expression for the Fourier transform of the solution in each half-plane, obtaining the transform function through splitting of an algebraic Wiener-Hopf-type equation of a complex variable.
The Wiener-Hopf solution given by Evans and Davies used the property that solutions, φ(y,z), of Equations (8) and (9) behave like

By subtracting the transmitted wave we define the function ϕ(y, z) by
Hence ϕ(y,z) has the property that ϕ(y,z) = O(1) as y → -∞ and is o(e-ky) as y → ∞. It follows that the Fourier transform of ψ(y, z) with respect to y,
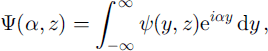
converges and is a regular function in the strip D = {-k < lma< 0}. Hence, ϕ(y, z) can be obtained by the inverse transform

for any τ, −k < r < 0 (cf Reference NobleNoble, 1958, ch. 2). It is convenient to actually solve for the corresponding vertical velocity ϕ z, and note that the same argument can be used to give an expression for ϕ z .
The Fourier transform of Equations (2–4) gives an algebraic equation relating the transforms of ψz, ![]() and
and ![]() in the respective half-planes,
in the respective half-planes,

For any ![]() , the relation is
, the relation is

where f1, f0 and c are analytic and non-zero in v.
The solution is called a "Wiener-Hopf technique" because at some stage a function k(α) is given that is regular and nonzero in the strip D of the complex a plane, and this function is decomposed into the form k(α) = k+(α)/k-(α), where each of k+ and K_ is regular and non-zero in D+ = {—k < Im α}, D_= {Im α < 0}, respectively. In this problem the ratio of the functions f1 and f0 in Equation (11) is decomposed into two functions K+ and K_ writing f1/f0 = K+/K-. Then, by simple algebraic manipulation, Equation (11) can be written as
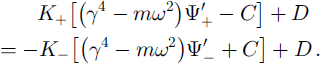
The lefthand side of Equation (12) is made regular in D+, and the righthand side of the equation is made regular in XL, by adding an appropriate function d to both sides. Since both sides are equal and regular in D, the Liouville’s theorem guarantees (Noble, Reference Noble1958) that both sides of Equation (12) equal a polynomial J (α), which in this case can be shown to be of first degree. Then solving Equation (12) gives *’± in terms of the polynomial j,

Hence the inverse transform of*’ gives the solution in terms of the two unknown constants defining J. The desired solution 4> can be calculated for arguments y > 0 by using the integral contour closed in the lower half a-plane and for y < 0 by using the contour taken in the upper half-plane. Note that φ and φz are continuous at y = 0 by construction.
The constants defining J (α) are computed by requiring that the solution for y > 0 satisfies the boundary conditions (Equation (5)) at y = 0. Since there are two conditions to be satisfied for this problem, this is consistent with the function J having two unknown constants, that is, J is polynomial of degree one.
In summary, the Wiener-Hopf technique for calculating the wave-ice interaction problem involves computation of the inverse of a 2 × 2 matrix, which has coefficients given by infinite summations of polynomials of the roots of the dispersion equations. We can easily incorporate more physical conditions of an ice sheet such as damping, thickness and compressive force as in Reference Balmforth and CrasterBalmforth and Craster (1999), as long as the ice-sheet equation remains a linear equation of φ. Additional terms slightly change the dispersion equations, and thus the positions of the roots, but have little effect on the basic structure of the solutions.
The deep-water case may be easily solved by noticing that the coefficients an and bn in Equations (8) and (9) are smooth functions of the wavenumbers λn and μn, giving evanescent modes, which become equally spaced as the water depth h tends to infinity. Therefore, the summations in Equations (8) and (9) become integrals of smooth functions over the imaginary axis. Furthermore, the integrands are simply combinations of the dispersion equations for the deep-water problem. Hence, they can be expressed by the residues and the poles of the integrands by the usual contour integration in the complex plane.
Summary
Note that the basic purpose of the two methods, the mode matching and the Wiener-Hopf technique, introduced in this section are the same in that they find the solution by enforcing continuity of the solution at the transition. The mode-matching method by Reference Fox and SquireFox and Squire (1990) uses direct numerical computation to obtain coefficients that give a continuous solution, while the Wiener-Hopf technique by Evans and Davies implements the same requirement by finding a Fourier transform function that is analytic at the transition in the complex domain, D, by solving the Wiener-Hopf Equation (11).
Computational Results
This section shows the results of computation of the reflection coefficient, R=|R|/|I|, and the transmission coefficient, t= |T|/|I|, using the modal expansion in Reference Evans and DaviesEvans and Davies (1968). The following results are given in non-dimensional form (or equivalently for ice with unit characteristic length) and for normalized water depths, 0.2^ and 2π. These depths correspond to shallow water and deep water, respectively. The results may be scaled for any ice thickness using the transformations in Equations (1).
Figures 2 and 3 show the reflection coefficient for various incident angles and frequencies in the cases of deep water (H = 2π) and shallow water (H = 0.2π), respectively. Note that for each incident-wave frequency, a critical angle exists, above which total reflection occurs. The reflection and transmission coefficients are computed using the formulas given in Reference Fox and SquireFox and Squire (1990). We found the formulas in Reference Evans and DaviesEvans and Davies (1968) were not suitable for numerical computation of the amplitude coefficients r, t and i, because the exponential functions caused numerical overflow. The dispersion equations (6) and (7) replace the exponential with the polynomials of the roots of the dispersion equations. Hence, all coefficients of the solution are a smooth function of the roots, particularly the summation over the evanescent modes, which enables us to compute the reflection coefficient and produce Figures 2 and 3 using the same formulas for any water depth.
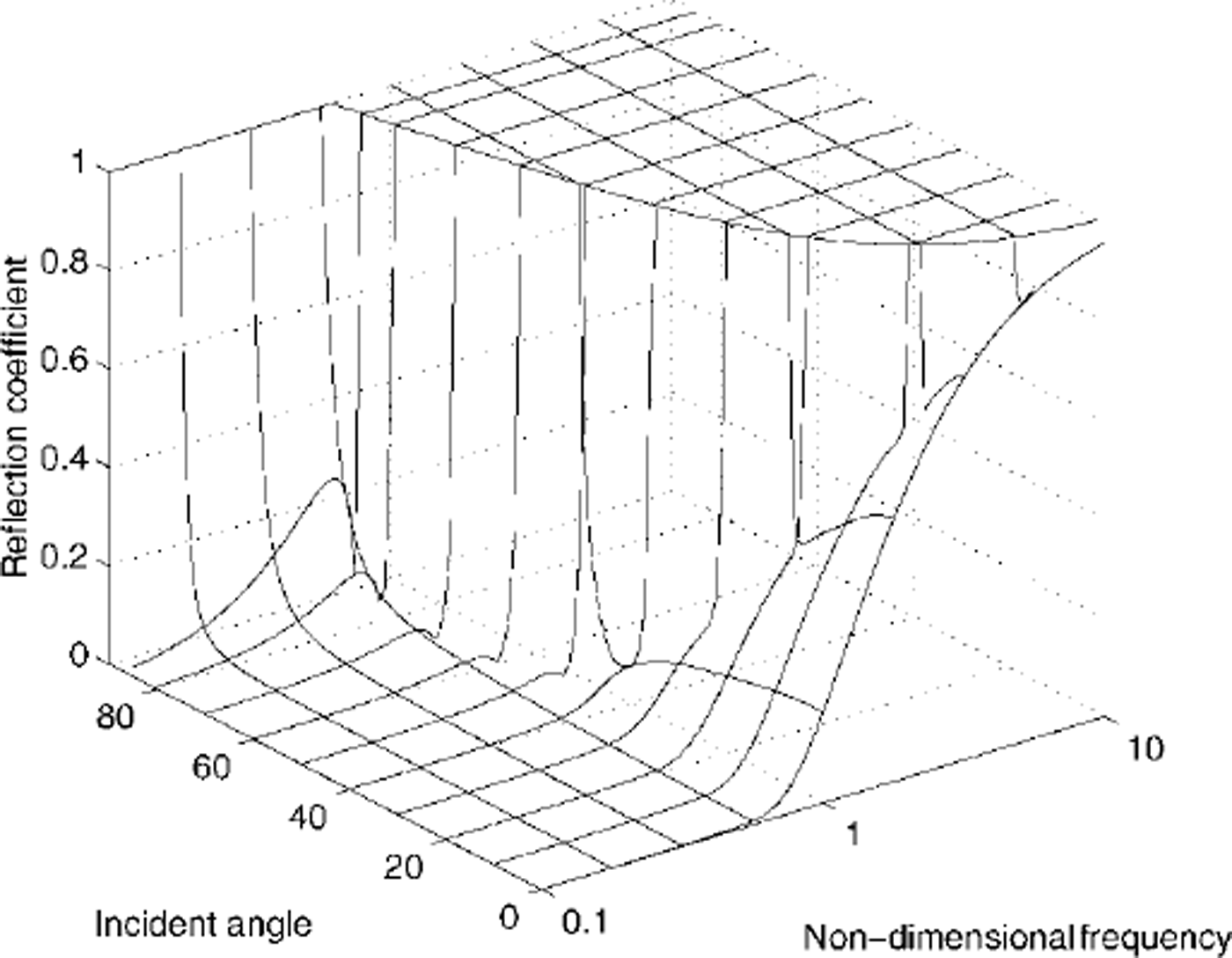
Fig. 2. Three-dimensional plot of reflection coefficient as a function of incident angle and radian frequency of the incoming wave. the ice sheet is floating on water depth of non-dimensional depth 2π (deep).
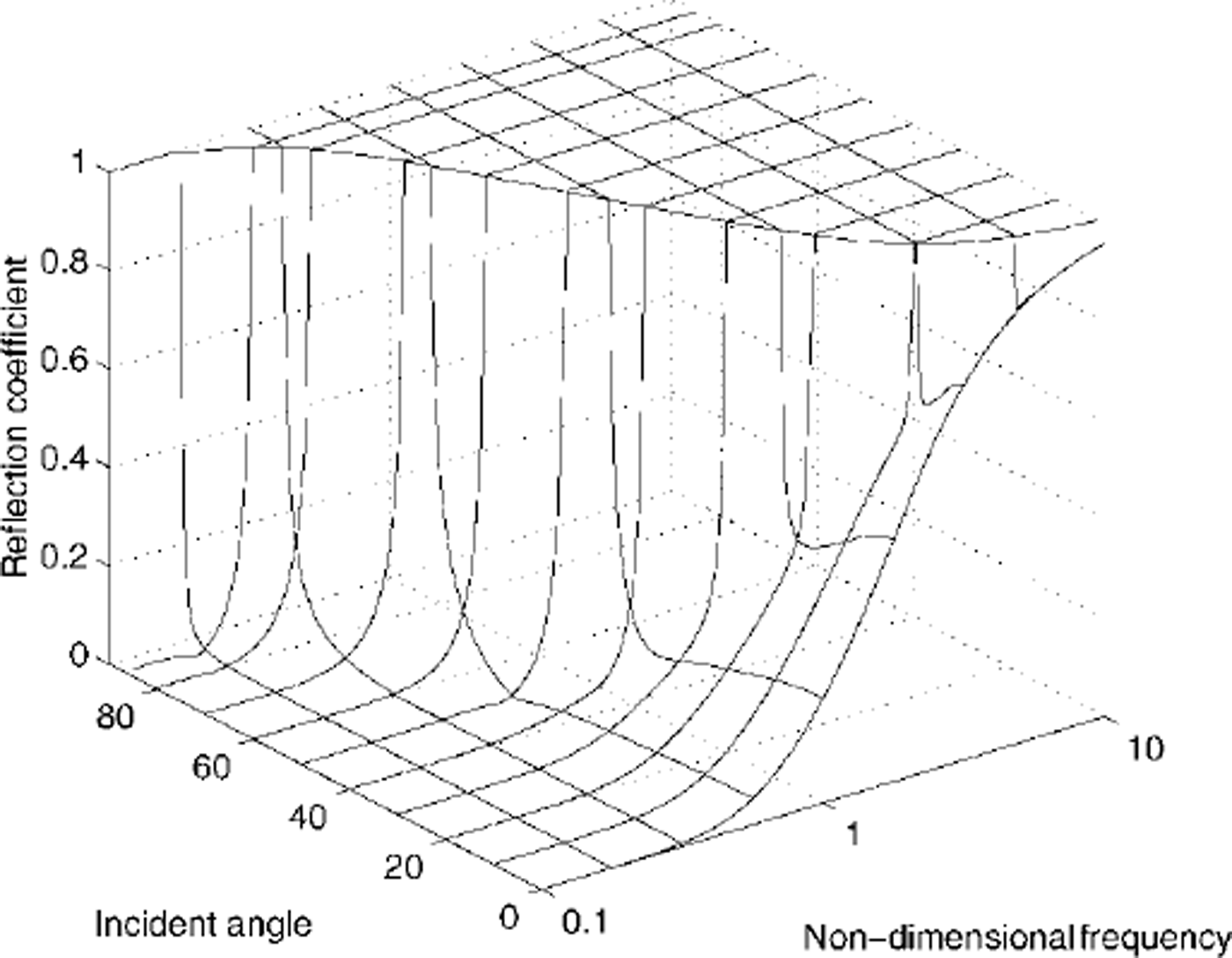
Fig. 3. Equivalent curves to figure 2 for non-dimensional water depth 0.2π (shallow).
Conclusions
Completion of the Wiener-Hopf technique developed by Reference Evans and DaviesEvans and Davies (1968) gives analytic expressions for the reflection and transmission of obliquely incident ocean waves. These expressions can be calculated simply and efficiently to give exact solutions. Although the mathematical procedure behind the Wiener-Hopf calculation is not as straightforward as it is for existing numerical methods, the fundamental philosophy of the technique is the same. The mode-matching method by Reference Fox and SquireFox and Squire (1990,Reference Fox and Squire1994) uses the fact that the velocity potential and its first derivatives are continuous; on the other hand, the Wiener-Hopf technique by Reference Evans and DaviesEvans and Davies (1968) uses the continuity of the solution in the Fourier space of complex variables. That both mode matching and the Wiener-Hopf technique express the solution by a sum over all natural modes with unknown coefficients has led to recent realization that the solutions given by Reference Evans and DaviesEvans and Davies (1968) can be numerically computed. The main advance is that we now know how to easily find the roots of the dispersion equations. We conclude that the computations actually required following the Wiener-Hopf analysis provide the simplest exact solution to the problem of ocean waves impinging on the edge of shore-fast sea ice.







