Introduction
Crevasses are usually thought to weaken an ice shelf. Many studies have investigated the different physical mechanisms by which crevasses originate, grow and penetrate the ice shelf (Reference Van der VeenVan der Veen, 1998a, Reference Van der Veenb), thereby causing calving (Reference Van der VeenVan der Veen, 2002) or large-scale collapse (Reference Scambos, Hulbe, Fahnestock and BohlanderScambos and others, 2000). This work has typically focused on the stress distribution in the vicinity of a single crevasse. Here we show that crevasses, collectively, can in fact be a source of mechanical resilience. Specifically, we analyze the normal-mode distribution and the small-amplitude, dynamical response of a model ice shelf containing a spatially periodic array of crevasses (Fig. 1). Numerical results show that the crevasse-ridden ice shelf has no normal modes from 0.2 to 0.38 Hz, a feature known as a ‘band gap’ in physics and mechanics literature. An ice shelf that has no crevasses (termed ‘intact’ hereafter) would have many elastic-flexural modes over the same frequency range. The modes that reside in the band-gap interval for an intact ice shelf are instead shifted to the edges of the band gap. The net effect is that the crevassed ice shelf has a large number of excess normal modes whose natural frequencies lie near the edges of the band gap. As a result, the response of a crevassed ice shelf has distinct peaks in the power spectrum, with peak locations corresponding to the edges of the band gap. When the ice shelf is driven at its seaward edge at a frequency that lies within the band gap, the ice-shelf motion is strongly attenuated as one moves away from the free edge. The behavior is reminiscent of an evanescent wave. Intriguingly, results from a recent study on the response of the Ross Ice Shelf, Antarctica, to ocean gravity wave forcing uncovered a peak near 0.5 Hz (Reference Bromirski and StephenBromirski and Stephen, 2012). Thus the band-gap feature studied here may be relevant for the mechanical response of real ice shelves (see also Reference McGrath, Steffen, Scambos, Rajaram, Casassa and Rodriguez LagosMcGrath and others, 2012).

Fig. 1. To assess how elastic-flexural waves propagate across a crevasse-ridden ice shelf (left), we analyze the normal modes of a model ice shelf (right).
There exists a variety of research on the propagation of classical waves through an infinite, periodic structure (Reference ShengSheng, 2006). The applications include crystallography, phononic crystals and electron transport in metals and semiconductors (Reference Ashcroft and MerminAshcroft and Mermin, 1976). Within the geophysical sciences, band gaps have been used to explain the formation of nearshore, underwater sandbars (Reference MeiMei, 1985) and gravity wave propagation through sea ice (Reference ChouChou, 1998).
In short, band gaps are possible whenever waves propagate through a periodic structure. To see why, consider how a transverse wave propagates along a one-dimensional string. This motion satisfies the linear wave equation and propagates at a uniform speed. However, when an imperfection is present (e.g. a bead fixed onto the string), the wave is partially reflected and partially transmitted upon encountering the bead. When a periodic arrangement of beads is placed along the string, the wave is reflected and transmitted partially every time it comes to a bead. Typically, when a large number of beads are present, the phases of the reflected portions of the wave are randomly distributed and do not add together. However, it is possible to arrange the wavelength of the transverse wave so that the phases of all the reflected waves arrive at the end of the string in phase with each other, thus adding constructively. In this special situation, the coherent backscattering channels almost all the energy of the incident wave into the reflected wave. In the limit of an infinite periodic array of beads along the string, the wave no longer propagates but instead becomes evanescent, i.e. decays exponentially with distance from the free edge.
The basic ingredients for this qualitative transition are simple: a periodic array of defects, a system whose lateral dimension is much larger than the spacing between the defects and, finally, the possibility of exciting a normal mode of the system whose wavelength is comparable with the spacing between the defects. The propagation of elastic-flexural waves along crevasse-ridden ice shelves satisfies all these criteria, and therefore supports band gaps (as we demonstrate below). In the same spirit, we also analyze the dispersal of energy associated with seiches in a fjord when ice melange is present (Reference MacAyeal, Freed-Brown, Zhang and AmundsonMacAyeal and others, 2012) and show that, if the melange can be idealized by a periodic array of solid ice blocks, then a band-gap structure also exists for the normal modes of the fjord. In a sense, these two cases can be viewed as different limits of the same underlying problem of how wave energy propagates through an ice-covered sea surface.
Previous work on wave/ice-shelf interactions has focused on the low-frequency, long-wavelength limit dominated by the inertia associated with water motion beneath the ice shelf. In these works, the ice shelf is idealized as intact and simply modifies the normal stress boundary condition on the water surface (e.g. Reference Balmforth and CrasterBalmforth and Craster, 1999).We take the opposite approach and focus on elastic-flexural waves, which are higher in frequency. When a thin ice shelf overlies a deep layer of water, the dispersion relation for shelf motion has the form
where f is the vibrational frequency, D = Eh 3 =12(1 − ѵ 2) is the flexural rigidity, E is the Young’s modulus, ѵ the Poisson ratio, k the wavenumber, ρ w the density of water, ρ i the density of ice and h the shelf thickness (Reference Landau and LifshitzLandau and Lifshitz, 1986). For the propagation of short-wavelength, elastic-flexural waves (hk ≫ 1), the coupling between water motion and shelf motion becomes irrelevant and the dispersion relation simplifies to
This is the dispersion relation of a thin elastic plate vibrating freely under a balance of elastic stresses and inertia. Motivated by this limiting behavior, we opt to neglect the normal stress exerted by the water motion below the ice shelf in our model calculation. Instead, we simply model the wave/ice-shelf interaction as an oscillatory displacement at the seaward edge of the ice shelf.
Problem Set-Up
Figure 1 illustrates the model ice shelf we analyze. The two-dimensional (2-D) shelf is 50 km in length, 300m thick and has basal crevasses spaced 500m apart. (For clarity of display, we omit most of the crevasses in the schematic.) These are length scales typical for an ice shelf. The left edge corresponds to the grounding line while the right edge intrudes into the ocean. For simplicity, we assume that the displacement vanishes along the left edge and that the elastic stresses vanish along the right edge. The crevasses are modeled as rectangular notches into the ice shelf, with each crevasse 150m in depth. The Young’s modulus of the ice shelf is 1GPa, the Poisson ratio is 0.3 and the density is 1000 kgm–3.
The elastic flexural modes satisfy the equation
where u(x, y, t) is the displacement of the ice shelf. The left-hand side of Eqn (3) corresponds to the inertia of the ice shelf, while the right-hand side describes elastic stresses. The first term on the right-hand side is primarily associated with transverse, or bending, modes, while the second term is associated with longitudinal modes. We use a coordinate system where x is the horizontal distance along the 2-D shelf and y is the vertical coordinate. To specify the normal modes completely requires boundary conditions. Since the purpose of this calculation is to assess the leading-order effect of crevasses on the mechanical response of an ice shelf, we opt to impose highly idealized boundary conditions. The left edge of the ice shelf is taken to be the grounding line and prescribed to have zero displacement. The right edge, as well as the top and bottom surfaces of the ice shelf, experiences zero tangential and normal stresses. (Preliminary work, not included here, shows that more realistic choices (e.g. introducing hydrostatic pressure) do not change the qualitative outcome.)
Results
We present two types of results, characterizing how the presence of a periodic array of crevasses changes the mechanical response of an ice shelf. We first assess the effect crevasses have on the normal-mode spectrum. In this approach, instead of analyzing how a specific wave disturbance propagates along a crevasse-ridden shelf, we use the fact that the wave disturbance can be thought of as a sum of normal modes. These correspond to standing waves, or elastic-flexural vibrations, of the ice shelf. Our key finding is that the dispersion curve of a crevasse-ridden ice shelf is qualitatively different from that of an intact ice shelf free of crevasses. The dispersion curve describing the wavenumber/ frequency relation is not continuous, reflecting an even distribution of normal modes as a function of f , but instead has frequency intervals where no eigenmodes exist, i.e. a band gap. Second, we demonstrate (via a direct simulation) that forcing the ice shelf at a frequency within the band gap elicits a qualitatively different response from the response when the gap is absent. All the numerical calculations were performed using COMSOL.
The impact on the normal-mode distribution, being more general, is the more powerful result. We describe the results in two steps. First we describe the results from a conceptual demonstration, where the ice shelf has only five crevasses. This will help build intuition for the results we obtain for the more realistic case. In our model, the presence of the crevasses only changes the geometry of the ice shelf. It does not directly change the stress along the ice-shelf boundary. However, the crevasses do indirectly affect the stress distribution, since a section of the ice shelf with a crevasse in it bends more readily. Intuitively, this means there exists a potential synergy between the crevasse locations and the antinodes of an elastic-flexural wave along the ice shelf. If every antinode of the wave coincides with a crevasse, then the elastic energy of the vibration can be lowered by leaving the long stretches of the ice shelf between the crevasses nearly straight at the price of bending the small region near the crevasses more strongly. This results in a waveform which is not sinusoidal, but instead has a ‘sawtooth’ shape. Figure 2 shows that, for a five-crevasse ice shelf, this occurs for the sixth normal mode. (The transverse modes are ordered by frequency, with the lower frequencies showing up first.) As contrast, we show also in Figure 2 the seventh normal mode. This mode is essentially unaffected by the crevasses, since they lie at nodes of the waveform, where the displacement is zero.
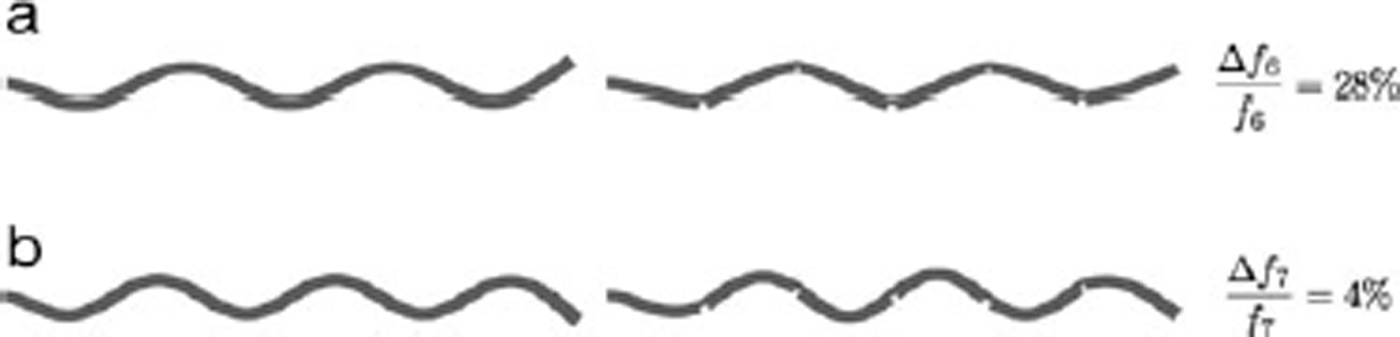
Fig. 2. Conceptual demonstration calculation, illustrating how the presence of crevasses in an ice shelf causes its normal-mode frequencies to become unevenly distributed. (a) The locations of the five crevasses coincide with the antinodes, the positions of maximal displacement, of the sixth normal mode. (b) In contrast, the crevasse locations coincide with the nodes, the positions of zero displacement, of the seventh normal mode. (In order to display the shape of the transverse modes clearly, we have vastly exaggerated the amplitudes of motion. All the calculations assume that the displacement amplitude is much smaller than the ice-shelf thickness. The distortions in the shape of crevasses are display artifacts and not included in our normal mode calculation.)
Since the presence of the crevasses essentially reduces the stiffness, or ‘spring constant’, for transverse vibrations of the ice shelf, one expects that the natural vibrational frequencies of all the normal modes will decrease when the crevasses are present. But what makes the effect nontrivial and interesting is that the frequency of adjacent eigenmodes is modified by rather different amounts. The synergy between the crevasse location and the antinode location causes the vibrational frequency of the sixth normal mode to decrease by 28%. In contrast, the vibrational frequency of the seventh normal mode decreases only by about 4%. As a result, the normal modes of an ice shelf with crevasses become unevenly distributed as a function of frequency.
The scenario described above suggests that the crevasses are expected to affect the normal-mode response most strongly when every crevasse location coincides with an antinode of the normal mode. Consider the fractional change in frequency given by ![]() , where Fn
is the frequency of the nth mode of an intact shelf and fn
is the frequency for a crevassed shelf. This quantity is largest when the normal mode’s wavelength is precisely double the spacing between the crevasses. In the five-crevasse problem, if we consider a normal mode with a shorter wavelength, say n = 20, then only a fraction of the antinodes would coincide with the crevasse locations. As a result, the waveform is less distorted from that for an intact ice shelf. The relative frequency shift is also smaller. The results of our simulation are consistent with this expectation.
, where Fn
is the frequency of the nth mode of an intact shelf and fn
is the frequency for a crevassed shelf. This quantity is largest when the normal mode’s wavelength is precisely double the spacing between the crevasses. In the five-crevasse problem, if we consider a normal mode with a shorter wavelength, say n = 20, then only a fraction of the antinodes would coincide with the crevasse locations. As a result, the waveform is less distorted from that for an intact ice shelf. The relative frequency shift is also smaller. The results of our simulation are consistent with this expectation.
Having examined the five-crevasse example, we now turn to results on the model ice shelf. In Figure 3 we display the dispersion curve, f (k), for an intact ice shelf with the same lateral extent and thickness as our model along with the dispersion curve for the model ice shelf. The two curves are qualitatively different. As for the five-crevasse problem, the presence of the crevasses causes the normal modes to be unevenly distributed. More importantly, we find that having a dense distribution of crevasses (having 100 crevasses over the ice shelf instead of merely 5) exaggerates the unevenness of the mode distribution. There is clearly a band gap from 0.2 to 0.38 Hz, corresponding to normal modes with wavelength of 1 km. These are the vibrational modes with nearly all the antinodes located near the crevasses and are therefore most strongly affected. The crevasse-filled ice shelf has no normal modes that vibrate with a frequency within that interval. In contrast, an intact ice shelf has many normal modes within this frequency range. Since the total number of modes does not change significantly when we change from an intact ice shelf to a crevasse-ridden ice shelf, the normal modes that span the band gap for an intact shelf are instead concentrated into the regions near the edge of the band gap. This is evident in the flattening of the dispersion curve, f (k), for the crevasse-ridden ice shelf, signifying that the edge regions support an unusually large number of normal modes with nearly identical natural vibration frequencies.

Fig. 3. Dispersion curves for an intact ice shelf (black) versus our model, crevasse-ridden ice shelf (blue). The flexural-wave normal modes of an intact ice shelf are distributed evenly in f , with the mode frequency increasing quadratically with the wavenumber, k. For a crevasse-ridden ice shelf, the dispersion curve has its first band gap from approximately 0.2 to 0.38 Hz. No eigenmodes of the system exist in this frequency range. In contrast, an intact ice shelf has many eigenmodes in this frequency range. Note also that the dispersion curve for the crevasse-ridden ice shelf flattens near the edges of the band gap. This feature means that the normal modes near the band-gap edge propagate significantly slower than their counterparts for an intact ice shelf.
In the limit of a shelf whose lateral extent is much larger than the spacing between the crevasses, the group velocities of these eigenmodes approach zero since f (k) is nearly horizontal near the edge. As a result, energy from the incident wave does not propagate into the ice shelf, but is instead reflected out into the ocean. This behavior is, mathematically, completely equivalent to the coherent backscattering scenario described for a propagating wave. The only difference is that in the normal-mode analysis it is natural to consider how crevasses interact with a standing wave, while the coherent backscattering scenario is the natural description for a propagating wave.
Finally, we assess how the band gap changes the response of an ice shelf to disturbances from ocean waves. We mimic the ocean-wave disturbance as a prescribed oscillatory displacement,
at the seaward edge of the ice shelf. Figure 4 contrasts the response for f = 0:1 Hz, a frequency outside the band gap and f = 0:3 Hz, a frequency inside. The times of the simulation snapshots are taken as (a) t = 303 s and (b) t = 297:7 s. These times are chosen so that the unperturbed waves in both simulations are given enough time to traverse the length of the ice shelf and return significantly. Slightly different times are taken so that the driving displacements have the same phase. When the disturbance frequency, f , lies outside the band gap (Fig. 4a), the response is qualitatively the same as that of an intact ice shelf. The edge disturbance excites elastic-flexural waves whose frequencies are close to the driving frequency. These waves initially travel from the seaward edge towards the grounding line, are reflected at the grounding line and travel back outwards towards the seaward edge. As a result, the whole ice shelf is set into oscillatory motion.
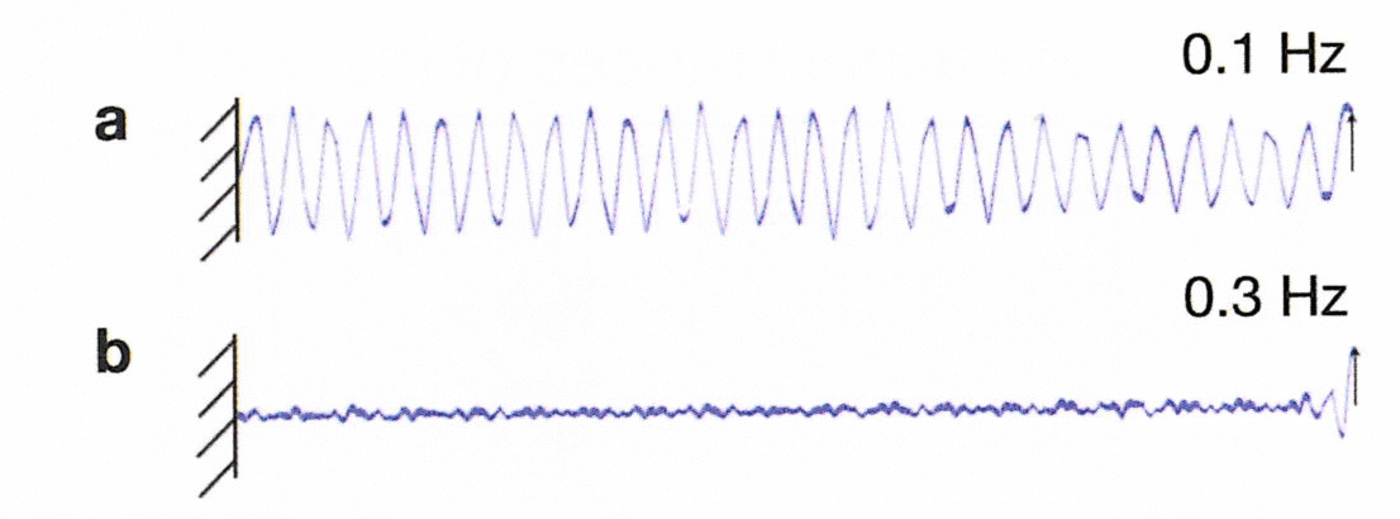
Fig. 4. Response of a crevasse-ridden ice shelf to prescribed oscillatory displacement of its seaward edge. We have exaggerated the amplitudes of the vertical displacement by the same scale factor in (a) and (b) in order to display the ice-shelf response clearly. (a) Response to driving frequency which lies outside the band gap: when the ice-shelf edge is oscillated at 0.1 Hz, which lies outside the band gap, the response resembles that of an intact ice shelf. The forcing excites several normal modes. The entire ice shelf vibrates with more or less the same amplitude. (b) Response to driving frequency which lies inside the band gap: when the ice-shelf edge is displaced at 0.3 Hz, which lies within the band gap, the forcing excites normal modes from the edges of the band gap. The amplitude of the ice-shelf motion attenuates strongly as we move away from the edge.
Inside the band gap (Fig. 4b), the response is very different. Since no elastic-flexural wave normal modes exist with natural frequencies near the driving frequencies, the response of the ice shelf is dominated by normal modes from the edges of the band gap. As a result, disturbances introduced at the ice-shelf edge propagate inwards very slowly. Over a longer timescale, the response of the ice shelf continues to be qualitatively different. The amplitude of the ice-shelf motion decays strongly as one moves away from the edge. Most of the ice-shelf interior is undisturbed. This striking attenuation, reminiscent of an evanescent wave, can be understood, at least qualitatively, as a consequence of the coherent backscattering effect described in the introduction. Each time an elastic-flexural wave hits a crevasse, it is partially transmitted and partially reflected. When the wavelength is mismatched with the spacing between the crevasses, the reflected waves from the different crevasses arrive at the seaward edge of the ice shelf with different phases, thereby interfering with each other destructively. When the wavelength of the normal mode is roughly twice the spacing between the crevasses, however, the reflected waves from the different crevasses can arrive at the seaward edge of the ice shelf in phase, thereby interfering with each other constructively. As a result, almost all the energy of the incident wave is reflected back into the ocean, instead of being dispersed through the ice shelf. In the limit that the ice-shelf extent becomes infinitely large relative to the spacing between the crevasses, the reflections from all the crevasses add constructively to create a true evanescent wave, one that decays exponentially with distance from the seaward edge. In reality, the number of crevasses on an ice shelf is large but finite, so the dynamical response only approximates an evanescent wave. Forcing the ice shelf at a frequency which lies within the band gap excites a response from the ice shelf, with the largest amplitudes from frequencies at the edges of the band gap.
If the ice shelf is exposed to a disturbance whose power is distributed evenly across a range of frequencies that span the band gap, then the response of the ice shelf will have distinctive peaks in the power spectrum, with each peak corresponding to one edge of the band gap.
Discussion
This work is a first attempt to quantitatively assess how the mechanical response of an ice shelf is altered by the presence of crevasses. To keep the analysis tractable, we chose to idealize the crevasses (which in reality are disordered, uneven in depth and variable in material properties) as spatially periodic and identical. We have checked that introducing a small amount of disorder, such as created by varying average spacing, does not change any of the main features reported here. We have also checked that (1) introducing a gentle taper in the ice-shelf thickness, (2) altering the shape of a crevasse from a rectangular notch to a wedge or (3) including the hydrostatic pressure term do not change our results. In short, the band gap is a robust feature and emerges whenever an ice shelf has a regular array of crevasses.
We see several future directions that naturally extend this work. First, we have included the wave/shelf interaction in the most simple manner possible, as an oscillatory displacement of the ice-shelf edge. It would be interesting to model the interaction more realistically by solving for the motion of the water under the ice shelf self-consistently with the ice-shelf motion. In this second scenario, the mechanical disturbance is not confined to the ice-shelf edge, but instead is distributed throughout the interior. This calculation may give us insight into how a crevasse-ridden ice shelf responds to tidal motion. Coupling the ocean and ice shelf will also give us a more precise indication of when the crossover occurs between a response dominated by water motion and one dominated by the inertia of the crevassed ice shelf.
Second, we emphasize that the emergence of the band gap in the dispersion curve depends fundamentally on a geometrical interplay between the wavelength of the elastic-flexural normal mode and the distribution of crevasses. Thus, disorder and variability, if sufficiently strong, will introduce qualitative changes. Works to characterize this second regime of dynamical response are underway.
Finally, the fact that the same ice shelf can respond in a dramatically different way, depending on whether it experiences an edge disturbance inside or outside the band gap may be relevant for ice-shelf collapse. To see why, let us suppose that the crevasse distribution on an ice shelf can evolve over a relatively long timescale so that, typically, the environmental disturbances perturb the ice shelf only within its band-gap range. If this assumed evolution exists, then a sudden thinning of the ice shelf may be catastrophic if the reduction in the ice-shelf thickness shifts the band gap appreciably, since the frequencies of the normal modes vary strongly with the ice-shelf thickness. Since forcing from the ocean waves is unchanged, a shift in the frequency interval for the band gap would switch the response of the ice shelf from the ‘within band gap’ response, in which most of the ice-shelf interior is shielded from wave disturbances, to the ‘out of band gap’ response, where the entire ice shelf experiences the effect of the waves. Testing this idea requires fieldwork that more fully characterizes the elastic-flexural wave response of ice shelves, as well as an understanding of whether, and how, crevasses evolve on an ice shelf.
Conclusion
The propagation of elastic-flexural waves through an ice shelf can be strongly modified by the presence of crevasses. We demonstrate this feature by calculating the normal modes of an ice shelf under the assumption that only inertia of the ice shelf and elastic stresses are significant. Unlike the case for an intact ice shelf, the normal modes for a crevasse-ridden ice shelf are unevenly distributed as a function of frequency. For a model ice shelf with dimensions and crevasse spacings consistent with field observations, there exists a ‘band gap’ from 0.2 to 0.38 Hz, an interval of frequency where no normal modes are possible. This behavior contrasts sharply with a crevasse-free ice shelf, which supports many normal modes within that frequency range. This band-gap structure gives rise to a qualitatively different mechanical response. Driving a crevasse-ridden ice shelf at its seaward edge with a frequency in the band gap causes the disturbance to be confined near the edge of the ice shelf, reminiscent of an evanescent (non-propagating) wave. Most of the interior of the ice shelf is left quiescent. In contrast, a crevasse-free ice shelf shows a response that is evenly distributed throughout the interior. More generally, the existence of a band gap implies that the response of a crevassed ice shelf exposed to wave forcings that cover a broad frequency range should show peaks in the power spectrum, with each peak corresponding to one edge of the band gap.
Acknowledgements
We thank Dorian S. Abbot, Justin C. Burton, L. Mac Cathles IV, Nicholas Guttenberg and Sidney R. Nagel for encouragement and insightful feedback. This work is supported by the US National Science Foundation under grants ANT-0944193, OPP-0838811 and CMG-0934534. J.F-B. was supported by the Materials Research Science and Engineering Center at the University of Chicago (DMR-0820054).






