1. Introduction
At present there are several comprehensive and advanced three-dimensional (3-D) methods for the analysis of snow. These methods include techniques such as X-ray microtomography, originally developed for medical purposes. While providing thorough physical information about snow structure, these methods require somewhat elaborate equipment which cannot easily be used in the field. For this reason, two-dimensional (2-D) snow-grain analysis remains an effective technique. Samples may be analyzed directly in the field or in the laboratory. Numerical snow-cover models used for avalanche forecasting, such as SNOWPACK (Reference Bartelt and LehningBartelt and Lehning, 2002; Reference Lehning, Bartelt, Brown and FierzLehning and others, 2002a,Reference Lehning, Bartelt, Brown, Fierz and Satyawalib) are based on 2-D grain analysis.
The methods utilize digital images of disaggregated samples of snow grains. The images have to undergo several stages of image processing before being segmented. The outlines of the snow grains can then be extracted and used as the source of all the quantitative information available for each snow grain.
Spline approximation for curvature measurements (see S. Hermann and R. Klette, http: //doi.ieeecomputersociety.org/10.1109/ICCTA.2007.2) as well as estimators for length and area (see, e.g., Reference Sladoje, Nyström, Saha, Nystrom, Sanniti di Baja and SvenssonSladoje and others, 2003) are classical problems in image processing. While methods are often assessed using simple shapes, snow grains may exhibit quite complex contours, and a comprehensive assessment of the currently available tools is still lacking.
There are several well-developed shape descriptors already used for snow grain classification. Dendricity, the ratio of the square of the perimeter of a grain to its area, is used to indicate the complexity of the grain outline. Sphericity (Reference Lesaffre, Pougatch and MartinLesaffre and others, 1998) and zero curvature (Reference Fierz and BaunachFierz and Baunach, 2000), which are designed to distinguish between faceted and rounded grains, are both based on curvature measurements. Curvature is itself a very useful shape descriptor (Reference Cesar and da Fontoura CostaCesar and da Fontoura Costa, 1997; Reference da Fontoura Costa and Cesarda Fontoura Costa and Cesar, 2001). Despite its usefulness, the accurate calculation of the curvature of digital contours has proven to be difficult, mainly because of the noise and distortions that are an inherent feature of digitally sampled signals. Errors ranging from 1% to >500% have been reported with respect to the application of standard techniques in the estimation of the curvature of circular contours (Reference Worring and SmeuldersWorring and Smeulders, 1993). Despite these difficulties, some studies have used the distribution of curvatures to gain even more information about snow samples (e.g. to distinguish between wind-transported snow and new snow deposited under calm conditions (Reference Guyomarc’h, Mérindol and SivardièreGuyomarc’h and Mérindol, 1995)).
The aim of this paper is to present some of the techniques which have been developed for the quantitative 2-D analysis of snow grains. Curvature of snow grain contours can be measured using a parabola-fitting method as described in Reference Lesaffre, Pougatch and MartinLesaffre and others (1998) and Reference Fierz and BaunachFierz and Baunach (2000). However, a cubic smoothing spline can also be used to generate smooth outlines from which the curvature can be evaluated. Furthermore, spline outlines can be used to evaluate both the perimeter and area of snow grains. These two parameters have previously been calculated using closed-source commercial software, and the algorithms for performing these calculations were not explicitly defined. We therefore use an all-in-one package providing both image processing as well as numerical tools to estimate the shape descriptors of interest.
The methods developed for calculating shape descriptors for snow grains are then tested. First we use synthetically generated single shapes for which the shape descriptors are known to quantitatively assess the methods. Second, well-characterized samples of disaggregated snow grains are used to show how effective various shape descriptors are at classifying different snow types. Finally, we attempt to use new descriptors to augment the classifying power within the group of dendritic snow grains, namely precipitation particles and decomposing and fragmented precipitation particles.
2. Methods
2.1. Outline extraction
We developed a MATLABTM-based graphical user interface to process images and calculate all relevant parameters from the extracted contours, avoiding proprietary codes. Whole snow grains or crystals were arranged on a small glass slide and then photographed from above, creating 2-D projections of the grain objects. All of the images were digitized at resolutions ranging from approximately 100 to 200 pxmm − 1 (i.e. pixels per millimetre). In a process referred to as segmentation, the images were converted from 8-bit greyscale images to binary images to extract the snow grain outlines. Before the segmentation process can be performed, background extraction, sharpening and smoothing techniques are first applied to pre-process the images (Reference JähneJähne, 2002). The threshold for segmentation is then manually set, and the greyscale images are thresholded into binary images. The discrete outlines of the grains are now easily extracted from the binary image. Manual editing of the outlines can be performed after thresholding if necessary. The outlines are then ready for analysis.
A cubic spline can be used as a smoothing interpolator to produce smooth grain shapes from the discrete outlines extracted from the original images. Full descriptions of the application, mathematics and algorithms governing splines are given by Reference de Boorde Boor (1978) and Reference DierckxDierckx (1993). A discrete grain outline C may be parameterized in terms of arc length s and represented in Cartesian coordinates by C(sn ) = (x(sn ), y(sn )), where n is the vector index of x and y. The smoothing spline f (s) then minimizes the expression
where N is the number of points in the outline and p is a parameter referred to as the smoothing coefficient.
The first term in Equation (1) is a standard measure of squared distances while the second term is a roughness measure. When p = 1, the second term of Equation (1) disappears so the spline is bound only by the condition of minimizing the distance between the spline curve and the original outline points. When applied to sets of closed outline points, this corresponds to a ‘natural’ cubic spline because the spline is forced to pass through all of the original points (Reference de Boorde Boor, 1978). When p = 0, the first term of Equation (1) disappears so the spline is bound only by the condition of minimizing the roughness measure term. Since the second derivative of the spline function is effectively a measure of the curvature, minimizing the second term of Equation (1) requires that the curvature of the spline outline be minimized at all points on the curve. The result is therefore simply a linear least-squares fit, as a straight line effectively has a curvature of 0.
For a particular outline shape, a simple increase of scale changes the relative balance of the two terms in Equation (1). The curvatures of a shape are inversely proportional to its scale. An increase of scale therefore decreases the curvature of a shape by a factor proportional to the scale of the shape. As the second derivative of the spline function is effectively a measure of curvature, the second term of Equation (1) can be adjusted to account for this scale-related curvature change. Square curvature is inversely proportional to the square of the shape scale. The total arc length s will also increase linearly with scale, hence the integration path also increases in the same way. The distance measure term of Equation (1) will also increase with the square of scale.
To eliminate scale-induced changes to both terms of Equation (1), we must therefore multiply by a weight factor proportional to the cube of the shape scale. This weight factor is denoted λ in Equation (1) and is simply the cube of the maximum diameter of the particle outline (in pixels) multiplied by a fixed constant of proportionality. Tests performed on synthetic shapes showed that once this weight factor was included, changes of scale had no effect on the behaviour of the spline. For any outline shape and a fixed value of p, altering the size of the discrete outline had no effect on the characteristics and degree of smoothness of the resulting spline outline. The remaining parameter to be selected from one grain to another was the smoothing coefficient p.
2.2. Curvature
Curvature is a fundamental shape descriptor used for a variety of shape analysis problems (Reference da Fontoura Costa and Cesarda Fontoura Costa and Cesar, 2001). The curvature of a plane curve given by Cartesian parametric equations x = x(t) and y = y(t) is defined by
where φ is the angle between the tangent to the curve and the x axis, and s is the arc length. Although the above equation does not provide a means to calculate the curvature of an outline, from it we can derive
where ẋ , ẍ, ẏ and ÿ are the first and second derivatives of x and y with respect to t , respectively. Curvature has units of inverse distance: either pixel − 1 or mm − 1 in the case of discrete outlines.
2.3. Curvature measurement
The parabola method is the current standard for curvature calculation of snow grain outlines. It is based on a routine described in Reference Lesaffre, Pougatch and MartinLesaffre and others (1998). The curvature at every pixel in the discrete outline is calculated. At each pixel it utilizes a section of the outline comprising the pixel of interest and N p pixels either side of that pixel. This outline section must then be rotated by angular increments into the most horizontal orientation before the parabola can be fitted. After extensive testing on a complete range of outline sections, the most versatile and effective method for choosing the most horizontal orientation was found. The technique aimed simply to find the orientation with the largest difference in x coordinates between the start and end points of the outline section. This method proved effective even for sharp corners and other difficult outline sections where other methods failed.
While Reference Lesaffre, Pougatch and MartinLesaffre and others (1998) used rotation increments of π/4, Reference Fierz and BaunachFierz and Baunach (2000) used 2π/31. The latter value is used in this study. The method then fits a parabola to the outline section in this rotated system and evaluates the curvature κ at the origin for x(t) = t and y(t) = at 2 + bt according to Equation (2):
A cubic spline is ideal for curvature measurement, as it has well-defined and continuous curvature at all points, by nature of its construction. Furthermore, problems stemming from low sampling resolutions may be overcome by the use of the spline to evaluate curvature at many more points than just the pixel locations of the discrete outline. While useful, this feature is unable to reveal the small details that can be lost when a snow grain is sampled at a low digital resolution.
We now introduce a parameter which is equal to the mean of the positive curvature values of a snow grain outline, the mpk. The mpk of a spline contour can be used as a means of selecting the most effective smoothing coefficient value p for a particular grain outline (see section 2.1). The mpk is evaluated for the complete range of smoothing coefficients 0 < p < 1. When mpk is plotted against p (Fig. 1), an extended region of vanishing or 0 gradient is sought. The p value corresponding to this region was found to yield outlines which were smooth and free from pixel-induced high-frequency noise. This p value represents the best estimate of the point at which the outline is settling into some kind of stable state. This technique was necessary because the ideal p value varied for different grain shapes.

Fig. 1. No-gradient method to find optimal smoothing coefficient p. The dashed line shows the p value chosen by seeking the region of lowest gradient on the mpk vs p curve. The dotted line shows the p value corresponding to the spline outline which yielded the lowest error in the mpk calculation.
Simple shapes required a large amount of smoothing due to the larger number of redundant pixels, i.e. pixels that were not entirely necessary to make a complete definition of the shape. As an extreme example, a circle could be defined using a very large amount of smoothing and only four outline points. More complex shapes, however, require less smoothing because the majority of the points in their outlines play a fundamental role in defining the features of the shape. For these shapes, the priority is shifted more towards adherence to the discrete points than smoothness. Once this p value has been found, the resulting smooth outline yields the maximum available amount of information about the characteristics of the shape at that given image resolution.
Figure 2 shows the resulting spline from both the no-gradient p value and the p value yielding the minimum error in the calculation of mpk. The spline curve produced using the no-gradient method is free from pixel-induced noise but, as a result of this smoothness, underestimates curvatures at sharp, high-curvature regions. The spline which gives the lowest mpk error can be seen to exhibit features that are not part of the grain shape but result from the high-frequency noise produced when the grain outline is forced onto an integer-valued pixel grid.

Fig. 2. Spline outlines for (a) no-gradient method and (b) p value yielding minimum mpk error. Original (dash-dot line) and discrete contours (open squares) are also shown. The discrete contours show pixels which are regarded as being inside the object after segmentation.
Other methods of curvature estimation from discrete curves can be found in S. Hermann and R. Klette, http: // doi.ieeecomputersociety.org/10.1109/ICCTA.2007.2.
2.4. Perimeter and area
The perimeter of a snow grain is defined as the length of the closed curve which encloses it. However, simply summing the distances between adjacent pixels along the discrete outline will overestimate the perimeter, the error growing as theresolution increases. This problem can be overcome either by using stereological methods based upon Crofton’s theorem (Reference SantalóSantaló , 2004) or by using a smooth continuous curve.
The area of a snow grain is defined as the area of the 2-D region enclosed by its boundary. Simply counting the number of pixels within the grain boundary will yield a value which rapidly approaches the exact area, obtainable by increasing the resolution sufficiently. Two methods for area measurement were assessed. The first was a zero-order geometrical moment calculation (Reference Seul, O’Gorman and SammonSeul and others, 2000). The second was a standard MATLABTM binary object area computation function (Reference PrattPratt, 1991). The latter method was found to be more accurate when tested on all synthetic shapes and was therefore chosen as the method best suited for snow grain area measurement.
2.5. Shape descriptors
2.5.1. Sphericity
The sphericity spg of a snow grain is defined as
where σκ
+ represents the standard deviation of the positive curvature values of the outline and ![]() represents the mean of the positive curvature values of the outline (mpk).
represents the mean of the positive curvature values of the outline (mpk).
The sphericity is designed to distinguish between rounded and faceted grains. A rounded grain will tend to have similar convex (positive) curvatures for a large proportion of the points in its outline, therefore its positive curvature distribution will tend to have a low standard deviation. Faceted grains, however, are usually comprised of very low- or even zero-curvature straight sections as well as of sharp corners of high curvature. This means there is a much greater spread in positive curvature values and hence the standard deviation is higher for this grain type. The sphericity expresses these differences in curvature characteristic: rounded grains with low σκ + and high mpk will tend to have a low sphericity whereas faceted grains with high σκ + and low mpk will tend to yield high sphericity values.
The sphericity for a sample was calculated by evaluating both σκ
+ and![]() over all positive curvature values from all grains, yielding the sample’s total sphericity spt . This parameter can initially appear somehow inverted because a circle would ideally have a sphericity of 0. Reference Lesaffre, Pougatch and MartinLesaffre and others (1998) therefore proposed the following regime to map spt onto the closed interval [0,1]:
over all positive curvature values from all grains, yielding the sample’s total sphericity spt . This parameter can initially appear somehow inverted because a circle would ideally have a sphericity of 0. Reference Lesaffre, Pougatch and MartinLesaffre and others (1998) therefore proposed the following regime to map spt onto the closed interval [0,1]:
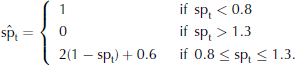
With this mapping, rounded grains should give a sp̂t value of 1 (being similar to spheres) and faceted grains should give a sp̂t value of 0. This mapping could lead to incorrect results if a particular sample was composed of rounded grains of a non-uniform size distribution. However, because the mapping utilizes a high threshold value below which the total sphericity is set to 1 (see Equation (4)), a sample of rounded grains would have to contain a very wide range of grain sizes to show a sphericity of <1. Such non-uniform grain-size distributions are generally only found in samples of new snow, i.e. precipitation particles as well as decomposing and fragmented precipitation particles (Reference ColbeckColbeck and others, 1990). For such samples, however, the sphericity is not such a relevant parameter as it is primarily designed to distinguish between faceted and rounded grains.
2.5.2. Zero curvature
The zero curvature zcg of a snow grain represents the percentage of contour pixels in which the curvature is found to be within a small range (±r) of 0. Given a small enough range, this represents the percentage of straight portions on the grain contour (Reference Fierz and BaunachFierz and Baunach, 2000). Indeed, it is rare that a curvature of exactly zero will be calculated for any particular point on a grain outline, due to pixel-induced distortions. As with sphericity, this parameter allows faceted and rounded grains to be distinguished, as faceted grains tend to be composed of longer straight sections. To avoid scale dependency in zero-curvature measurements, curvature values must be expressed in mm − 1, thus requiring a calibration factor. As for sphericity, it is better to evaluate the total zero curvature zct over all curvature values N from all grains from a particular sample as
where
Reference Fierz and BaunachFierz and Baunach (2000) chose r to be 0.05 mm − 1, but no demonstration on how this choice affects the calculation was given. The same authors also argued that samples of fully faceted snow grains gave values for zct > 1.4%, and that fully developed depth hoar was consistently observed for values >2.5% (Reference BaunachBaunach, 1999). However, no mapping onto the closed interval [0,1] has been proposed so far.
2.5.3. Dendricity
The dendricity ddg of a snow grain is defined as
where P is grain perimeter and A is grain area. This parameter aims to distinguish between new, fragmented and decomposing snow grains (dendritic grains) and older, fully decomposed snow grains (non-dendritic grains). The principle of this parameter is that dendritic grains, with their characteristic branches and dendrites, tend to have a large perimeter and a relatively small area. Non-dendritic grains, however, tend to have much simpler shapes with a larger area and smaller perimeter. A perfect circle has a dendricity of 1, whereas a new snow grain yields values of up to 20 or more. For a complete sample containing small grains, Reference Lesaffre, Pougatch and MartinLesaffre and others (1998) found this parameter to be more effective as a sum over all grain perimeters and areas, i.e.
Reference Lesaffre, Pougatch and MartinLesaffre and others (1998) also used the following regime to map this total dendricity ddt to the closed interval [0,1]:
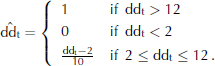
However, it is not clear whether d̂dt is able to efficiently discriminate further between samples containing either new snow, decomposing precipitation particles or both.
2.5.4. Density functions
Density functions of curvatures either over all pixels or per grain as well as of dendricity per grain may also convey additional information about the shapes we want to characterize (see, e.g., Reference Guyomarc’h, Mérindol and SivardièreGuyomarc’h and Mérindol, 1995).
3. Shapes And Snow Samples
3.1. Synthetic shapes
We use a small set of synthetic shapes to assess the methods, comparing results with known values for shape descriptors. The two parametric functions

where r is the radius of the shape at angle θ and z is a scaling factor, generate a rounded hexagonal and a dendritic shape shown in Figure 3. We use an angle index of 106 equally spaced values for θ in the closed interval [−π, π] to draw the shapes, and can explicitly calculate perimeter, area and first and second derivatives for any value of θ. Curvature is evaluated from the derivatives according to Equation (2).

Fig. 3. Parametric shapes: (a) rounded hexagon; and (b) dendritic shape.
A further two shapes are generated by fitting a spline to a limited number of points taken from discrete, real snow grain outlines. Figure 4 shows the form of the two spline-generated outlines: a depth-hoar grain and a precipitation particle. Again, we can evaluate exact perimeter, area and curvature values for the above outlines.

Fig. 4. Digitized, spline-generated grain outlines: (a) depth hoar; and (b) precipitation particle.
The continuous outlines are sampled at a high resolution (20×) and the coordinates are used to produce a binary image of the shape. This image is then resampled back to the original resolution as follows. If more than half of the pixels in each 20 × 20 square are ‘on’ (have the value 1), then the corresponding single pixel in the new (1× resolution) image is set to 1; otherwise the pixel is set to 0. The discrete outlines are then extracted from this image using the same function as is used for real snow images. This process mimics the way real snow images are thresholded and outlined. Shape descriptors derived from either discrete or fitted continuous contours can then be compared with the exact values obtained from the original synthetic shapes. We also draw the shapes at various sizes, i.e. their largest extension, to investigate scale and resolution dependencies.
3.2. Snow samples
Reference Fierz and BaunachFierz and Baunach (2000) describe well-defined temperature-gradient metamorphism experiments performed in a cold laboratory. Here we use the pictures taken during two of these experiments that lasted 3 days each. Table 1 gives an overview of both experiments and samples. Each sample contained 100–270 individual snow grains. We use these well-characterized samples to look at the time evolution of shape descriptors.
Table 1. Characteristics of the two cold-laboratory experiments after initial settling (duration each 3 days)

We took images of new snow crystals collected in situ during various snowfall periods in 2006. The samples, which contained 27–114 grains, represent different mean wind conditions from 0.75 to 8.25 ms − 1. These samples help to explore the potential of chosen descriptors to discriminate between different stages of dendricity, from unbroken stellar and dendritic particles at low wind speed to highly broken crystals at high wind speeds.
4. Results
4.1. Synthetic shapes
A general trend was observed that the parabola method suffers from a strong scale dependence. The number of pixels used for the parabola fitting (2N p + 1) at each outline point must be selected (see section 2.3) and this choice has a fundamental effect on the resulting curvature values. For any particular value of N p, there exists an optimum curvature radius which the method will evaluate accurately. Curvature values far from this optimum value will be either under- or overestimated while a small range either side of this value will be evaluated with a reasonable degree of accuracy. This was observed for all synthetic shapes. Applying the parabola method to the synthetic depth-hoar shape and altering the size (equivalent to altering the resolution) reveals the scale dependence of the method.
Showing the percentage error in calculated mean positive curvature mpk relative to the known exact values, Figure 5 indicates that the optimum N p value for the synthetic depth-hoar shape is N p = 4, keeping errors in mpk <20% for all sizes except the smallest. For the rounded hexagon shape, however, N p = 9 was found to be optimum for all sizes with an error smaller than 15% (not shown). In general, errors increase with size for N p values smaller than the optimum, and the converse for larger N p values.

Fig. 5. Parabola method: percentage mpk error as a function of parabola-fitting value N p for synthetic depth-hoar grains of different sizes (in pixels).
Figure 6 shows corresponding results for the spline method. A minimum is reached for each size at different p values. We find the same behaviour for all four synthetic shapes. In addition, solid circles mark the errors for the optimized p values as determined by the no-gradient method (see section 2.1). Although these errors appear unexpectedly large for an optimized fit, it should be noted that the no-gradient method seeks outlines which are smooth and free from pixel-induced noise and distortions. In order to smooth out these artefacts, high-curvature regions are generally smoothed to a certain extent. The method therefore underestimates curvature values in these regions. However, the no-gradient method was found to be effective at producing smooth outlines which were well matched to the original grain shape (when plotted over the original real snow images). For these real grains, since we cannot compare calculated parameter values with their exact values, the most important consideration is how well matched the smooth spline outlines are with the grain shape on the original image.

Fig. 6. Spline method: percentage mpk error as a function of smoothing coefficient p for synthetic depth-hoar grains of different sizes (in pixels). The solid circles show the error for the p value found by the zero-gradient method.
To summarize our results for the four synthetic shapes, we present the errors for all the parameters of interest for a fixed size D of 140 px in Tables 2 and 3. We give the errors found for each method discussed above, using an N p value of 8 for the parabola method (P 8), the no-gradient method (S ng) and, for each shape, the p value which yielded the minimal mpk error (S min).
Table 2. Percentage errors for perimeter, area and dendricity per grain ddg relative to exact values for the synthetic shapes of size D = 140 px, measured using the spline with p values chosen using the no-gradient method
Table 3. Percentage errors for mean positive curvature mpk, standard deviation of positive curvature SDpk, sphericity spg and zero curvature zcg (all per grain) relative to exact values for the synthetic shapes of size D = 140 px

From inspection of Table 2, it is clear that perimeter and area measurements are reasonably accurate for all but the dendritic shape. The large error in perimeter measurement is due to two factors. First, the digitization process results in a large amount of detail being lost at the sharp, concave sections near the centre of the shape. Second, for a shape as dendritic as this, a distortion-free outline will inevitably smooth out high-curvature regions to a certain degree. As a result, measured perimeter values are generally underestimated for such complex shapes.
Table 3 shows that, in general, the spline method yields more accurate curvature measurements than the parabola method. It is interesting to note that even when the p value ( see section 2.3) which yields minimum mpk error for a particular shape is known (this is the case only for the synthetic shapes), other parameters show similar errors to those shown by the no-gradient method. This highlights the fact that while one p value may achieve a good result for one parameter, another p value could yield a more accurate overall distribution of curvatures.
4.2. Cold-laboratory experiments
Figure 7 depicts the evolution with time of total mean positive curvature mpkt, standard deviation of positive curvature and sphericity spt for the six samples analyzed during cold-laboratory experiment 6. The different filtering effects of the parabola (N p = 8, bandpass filter) or the spline method (no-gradient method, low-pass filter) can be clearly seen from the differences in mpkt values at all stages of the experiment. Indeed, the spline method yields larger mpkt values, being able to accurately measure a larger range of curvatures (and, in particular, high curvatures). Both methods show similar changes with time, however, and the decrease in mpkt reflects the growth from faceted to large depth-hoar crystals with longer straight portions and less high-curvature regions on their contour. The standard deviation follows a similar behaviour. Again, the spline method yields higher values, as the density function for positive curvature is expected to be broader due to the larger range of values measured. On the other hand, sphericity values are very similar for both methods. Note, however, that the mapped sphericity sp̂t is low (≤0.2) from the beginning of the experiment and has reached 0 at 1.5days (spt ≥ 1.3).

Fig. 7. Cold-laboratory experiment 6: (a) total mean positive curvature mpkt ; (b) standard deviation of mpkt ; and (c) total sphericity spt as a function of time.
The partly decomposed and dendritic precipitation particles composing the initial samples quickly recrystallize to faceted grains under the action of a temperature gradient of 350 Km − 1. Initial total dendricity ddt drops from >8 to <4 within the first day of the experiment, corresponding to mapped values d̂dt of ≥0.6 and ≤0.2, respectively. As may be expected, mean positive curvature mpkt as well as its standard deviation are high at the initial stage, and sphericity is near the threshold value for fully faceted grains, i.e. sp̂t ≤ 0.2.
Experiment 4 begins with small rounded grains subjected to a temperature gradient of 150 Km − 1. Snow density is 290 kgm − 3. From observation, we know that recrystallization to faceted grains is well developed after the first stage and proceeds to small depth-hoar crystals (size <0.75 mm). However, the recrystallized grains still show noticeable rounding and no typical striations of depth hoar. While these shape characteristics do not change much during the experiment, the size or maximal extent of the grains increases slightly to about 1 mm. This evolution is nicely reproduced by both d̂dt and sp̂t as shown in Figure 8. While d̂dt shows little or no change during the experiment as expected, sp̂t drops from an initial value slightly above 0.6 to slightly below 0.5 at the first stage of the experiment and decreases steadily afterwards but never seems to reach zero. Indeed, total sphericity spans the range 0.9 < spt ≤ 1.3 without ever crossing the upper threshold, contrary to experiment 6.

Fig. 8. Cold-laboratory experiment 4: (a) total mapped dendricity d̂dt and (b) total mapped sphericity sp̂t as a function of time.
4.3. New snow
Figure 9 shows the density functions of ddg for new snow samples collected at five different mean wind speeds (e.g. 3.75 (±0.25)ms − 1). The non-parametricWilcoxon rank-sum test reveals that the two density functions for wind speeds >4ms − 1 are significantly distinct from the three at lower wind speeds (95% level). Total dendricity ddt also indicates this break which is associated with the onset of saltation, i.e. mechanical fragmentation of precipitation particles. However, no further discrimination is possible within the two distinct ranges.

Fig. 9. (a) Total dendricities and (b) box-and-whisker plots showing the lower-quartile, median and upper-quartile value for new snow dendricity per grain ddg at five different mean wind speeds.
5. Discussion
A fundamental characteristic of the parabola method is that it exhibits a distinct scale dependence. For a particular N p value, curvatures within a small range around an optimum value will be measured accurately. Outside of this range, however, errors in measured curvature will increase. In a sense, the parabola method acts like a bandpass filter. If a shape does not exhibit a large range of curvatures (e.g. simple shapes) and the mpk of the shape is close to the optimum curvature value for the chosen N p, the parabola method should yield reasonable results. However, its accuracy can be reduced if the shape complexity is high. Complex shapes tend to exhibit a broader range of curvatures and the parabola method will therefore be unable to measure the entire range accurately with a fixed N p value. Even if the real mpk is close to the optimum curvature value for that particular N p value, the measured density function of curvatures will not reflect the real distribution because values away from the optimal range will be under- or overestimated. As stated previously, the method could be described as a filter through which values close to the optimal range pass easily and values which differ are blocked.
Depending on the grain shape and N p value, small details of the outline can be smoothed or, on the other hand, pixel-based artefacts can be intepreted as grain features. Therefore, choosing the most effective N p value is neither simple nor trivial. Reference Lesaffre, Pougatch and MartinLesaffre and others (1998) found N p = 8 to be optimum for isolated and overlapping circles. While this value yields reasonably accurate results for simple shapes (e.g. the rounded hexagon depicted in Fig. 3a), it is too large to efficiently measure the smaller features and high-curvature regions of more complex shapes. However, it is important to choose an N p value which is too high rather than too low. If the method inteprets pixel distortions as grain features, then the results will rapidly become unstable. If N p is too high, a simple underestimation of curvatures would be observed; however, an estimate of the underlying distribution would be reproduced with albeit lower magnitudes.
The cubic smoothing spline can provide valuable information for the distinction and characterization of snow grains. Firstly, it is an effective method for producing a smooth contour from a discrete pixel outline from which perimeter and area values can be evaluated. By using a weight factor proportional to the cube of the shape scale, the method was adapted to be completely invariant under changes of scale.
For measurements of curvature, the spline method bears a filtering effect similar to the parabola method. This can be observed most strongly on complex shapes. A certain amount of smoothing is crucial to eliminate pixel noise from the low-curvature regions of these shapes. It would be incorrect to use a method which consistently exhibited pixel-based artefacts in its outlines. With this amount of smoothing, however, the high-curvature sections of a complex outline will always be smoothed out to a certain degree. In this way, the spline method acts like a low-pass filter, reducing noise due to digitization but unveiling all features of interest at larger scales. One way to avoid this effect would be to use non-constant weight factors as additional inputs to the spline.
A first-guess outline could be constructed using the no-gradient method. Based on the curvature values of that outline, a weight factor could be constructed which altered the relative requirements of smoothness and point adherence depending on the position in the outline. Theoretically, successive iterations would yield more accurate results because the function would use more smoothing in the low-curvature regions, and the converse. However, such a technique would require extensive investigation before being made effective. For our datasets and resolutions, the no-gradient technique offers an effective way to choose the smoothing coefficient p, from which smooth, distortion-free outlines can be produced. Parameters such as total sphericity spt can then be applied, providing a satisfactory tool for a coarse classification of samples of disaggregated snow grains, as for experiment 4. On the other hand, mapping these quantities to a closed interval [0, 1] will reduce their usefulness, as information may get lost as in the case of experiment 6.
Although the spline method may act as a low-pass filter, it can nevertheless accurately measure a wider range of curvatures than the parabola method. The degree of accuracy with which the spline method can measure curvatures is generally dependent on the image resolution. If images with progressively higher resolutions were used, the spline method with a very large amount of smoothing would yield more and more accurate results. There would of course be some threshold resolution, above which no more information about the snow grains would be revealed. At this resolution it should be possible to have complete and fully accurate 2-D information about the grains. These data might then be compared with the analagous data from 3-D analysis.
Shape descriptors based on perimeter and area measurements are both more robust and more accurate (see Table 2). Nevertheless, total dendricity ddt does not allow for more than a coarse classification into dendritic and non-dendritic shapes. Unfortunately, analysis of the density functions for the per grain dendricities does not provide any extra advantage.
6. Conclusions
Methods for the characterization and analysis of 2-D snow grain images have been assessed. This assessment was conducted in the context of several well-established shape descriptors. The ratio of square of perimeter to area, known as the dendricity, allows the distinction of new snow from older snow. The ratio of standard deviation of positive curvature to mean positive curvature allows the distinction of faceted from rounded grains.
Two techniques for curvature measurement were compared: the parabola method (which is the current standard) and the spline method. The methods were tested using synthetic grain outlines which were then digitally sampled. The resulting discrete outlines from these synthetic shapes simulated both the form of real snow grains and the effects of digitization. The exact values for all necessary shape descriptors could be calculated exactly from these synthetic shapes before digital sampling. Results of this analysis showed the parabola method to be highly scale-dependent, showing characteristics of a bandpass filter. The spline method showed a low-pass filtering effect whereby high-curvature sections and small outline details were smoothed out to a certain extent. Errors in mean and standard deviation of positive curvature were found to be considerable for both methods, particularly for more complex grain shapes and shapes with more small details. The parabola method was optimized by choosing a parabola-fitting value of N p = 8. This same value was chosen by Lesaffre and others (1998). The spline method was optimized using a no-gradient technique to choose the smoothing coefficient p.
The methods were then applied to samples of disaggregated snow grains. These samples consisted of cold-laboratory experiments, in which the snow grains underwent metamorphism due to a constant temperature gradient which allowed the time evolution of the various shape descriptors to be analyzed. Sets of new snow samples taken at different mean wind velocities were also used to assess the ability of descriptors to distinguish different stages of grain decomposition and fragmentation.
The results showed that the sphericity is indeed capable of making a broad characterization of faceted from rounded grains. However, the mapping of these values can have different effects depending on the method and resolution used for the analysis. The total dendricity ddt was found to offer some effectiveness at showing the change in grain form from highly dendritic to fragmented particles.
Acknowledgements
This work is dedicated to J.-B. Brzoska, who contributed so much to the field of snow microstructure and acted as scientific editor of this paper before he unexpectedly passed away. Many other people also contributed to this work, but we would particularly like to thank F. Perret, J. Hendrikx, M. Connolly, R. Grant, C. Zwart and A. Clifton. Thanks also to M. Lehning for supporting this work over the years. S.J. Bartlett and A. Craig would like to thank both the University of Bath and the WSL/SLF for allowing them to fulfil their internship in Davos. The constructive comments of two anonymous reviewers helped improve this paper.






