Introduction
Seismic emissions associated with fracturing in ice masses are known as icequakes and have been subject to a number of different studies, such as the opening of crevasses (e.g. Reference Neave and SavageNeave and Savage, 1970; Reference BassisBassis and others, 2007; Reference Roux, Marsan, Metaxian, O’Brien and MoreauRoux and others, 2008), the study of basal conditions of Antarctic ice streams (e.g. Reference Anandakrishnan and BentleyAnandakrishnan and Bentley, 1993; Reference SmithSmith, 2006; Reference Winberry, Anandakrishnan and AlleyWinberry and others, 2009), changes in basal water pressure (e.g. Reference Walter, Deichmann and FunkWalter and others, 2008; Reference West, Larsen, Truffer, O’Neel and LeBlancWest and others, 2010) and iceberg calving (e.g. Reference O’Neel, Marshall, McNamara and PfefferO’Neel and others, 2007; Reference Rial, Tang and SteffenRial and others, 2009; Reference Walter, O’Neel, McNamara, Pfeffer, Bassis and FrickerWalter and others, 2010). If icequakes are sufficiently large (seismic magnitude >4), they may be detected and located using the global seismic network (e.g. Reference Ekström, Nettles and TsaiEkström and others, 2006; Reference Tsai and EkströmTsai and Ekström, 2007; Reference Chen, Shearer, Walter and FrickerChen and others, 2011).
Fundamental to the study of seismicity at any scale is the accurate location of a seismic event (e.g. earthquake). Traditionally, seismic events are located by assuming a fixed seismic velocity model and minimizing the differences between the observed and predicted arrival times of various phases at a number of receivers (e.g. Reference Lee and StewartLee and Stewart, 1981). In general, the traditional phase-picking method is suited to the location of individual events that are well separated in time and that generate impulsive onsets with a high signal-to-noise ratio. However, this method is susceptible to two main sources of error, (1) the mis-picking of the arrival onset (e.g. in low signal-to-noise environments) and, more serious, (2) the correct correlation of the individual arrival times with the correct seismic event, which becomes particularly difficult if multiple events are closely spaced in time (Reference Kao and ShanKao and Shan, 2004).
Glaciers are often seismically highly emissive, with tens to hundreds of events detected per hour (e.g. Reference Walter, Deichmann and FunkWalter and others, 2008; Reference West, Larsen, Truffer, O’Neel and LeBlancWest and others, 2010). The number of icequakes increases substantially, to a rate of several thousand events per hour, during iceberg calving (e.g. Reference O’Neel, Marshall, McNamara and PfefferO’Neel and others, 2007; Reference Walter, O’Neel, McNamara, Pfeffer, Bassis and FrickerWalter and others, 2010), in areas of serac falls (Reference Roux, Marsan, Metaxian, O’Brien and MoreauRoux and others, 2008) and during the drainage of supraglacial lakes (Reference DasDas and others, 2008). Passive seismic networks in glaciological studies are generally limited to ten or fewer stations, with an aperture of ∼1–2 km. The high rate of seismicity, the limited number of stations and the large network aperture can lead to spatial aliasing, making the correlation of the individual onset times with a particular event almost impossible. As a result, two approaches have been used to locate events in periods of high seismicity. The first approach uses cross-correlation, where a reference event is selected, allowing a catalogue of similar events to be built, by searching within the period of interest (e.g. Reference ShellyShelly, 2010). Once a catalogue has been built, the traditional arrival-time minimization method can be applied to locate the seismic events. The second approach uses migration-based algorithms to back-propagate waveforms in either time or space, assigning the hypocentre as the point of maximum energy. Migration methods include the minimization of measured and modelled seismic amplitude decay (Reference YamasatoYamasato, 1997; Reference Battaglia and AkiBattaglia and Aki, 2003; Reference Battaglia, Aki and FerrazziniBattaglia and others, 2005; Reference Taisne, Brenguie, Shapiro and FerrazziniTaisne and others, 2011), a source-scanning algorithm (Reference Kao and ShanKao and Shan, 2004, Reference Kao and Shan2007), the stacking of waveform envelopes (e.g. Reference Baker, Granat and ClaytonBaker and others, 2005; Reference Rentsch, Buske, Lüth and ShapiroRentsch and others, 2007) and semblance stacking (e.g. Reference Chambers, Kendall, Brandsberg-Dahl and RuedaChambers and others, 2010). While migration-based approaches are computationally expensive, they do not require arrival times to be picked and identified and are therefore well suited to locating weak and/or distal events with low signal-to-noise ratios (e.g. Reference Chambers, Kendall, Brandsberg-Dahl and RuedaChambers and others, 2010).
We present an automated approach for the location of seismic events using the decay of the seismic amplitude with distance from the source. The method is applied to allow accurate location of known seismic reflection sources using a network of six passive seismometers deployed on the Greenland ice sheet in 2010. The influence of varying amounts of ‘real’ ambient noise on the location of the seismic shots is then investigated. Finally we examine the ability of the method to image a synthetic fracture, mimicking rapid supraglacial lake drainage (e.g. Reference Alley, Dupont, Parizek and AnandakrishnanAlley and others, 2005; Reference Van der VeenVan der Veen, 2007; Reference Krawczynski, Behn, Das and JoughinKrawczynski and others, 2009; Reference Tsai and RiceTsai and Rice, 2010) with uncertainties in the forward model as well as variations in signal-to-noise ratio using the network geometry used on the Greenland ice sheet in 2010. The ability to monitor seismic swarms associated with hydraulic fracture provides a powerful method of tracking water movements and fracturing through the ice.
Event Location Method
We automatically estimate the source position by minimizing the difference between modelled and measured seismic amplitudes recorded across a network of sensors in a given time window. This method has been successfully applied to the location of volcanic tremors (Reference Battaglia and AkiBattaglia and Aki, 2003; Reference Battaglia, Aki and FerrazziniBattaglia and others, 2005; Reference Di Grazia, Falsaperla and LangerDi Grazia and others, 2006), the tracking of magma propagation in the formation of dykes (Reference Taisne, Brenguie, Shapiro and FerrazziniTaisne and others, 2011) and in imaging pyroclastic flow evolution (Reference YamasatoYamasato, 1997). The analogous mechanics of dyke/crevasse propagation results in similar volcanic and icequake waveforms being recorded (e.g. Reference O’Neel and PfefferO’Neel and Pfeffer, 2007; Reference West, Larsen, Truffer, O’Neel and LeBlancWest and others, 2010) and makes this approach well suited to the location of the latter type of seismicity.
Following Reference Battaglia and AkiBattaglia and Aki (2003) and assuming that the amplitude, A, decays smoothly as a function of hypocentral distance in a homogeneous half-space for a given frequency band, the amplitude as a function of hypocentral distance, A(r), can be calculated as
where
In Eqns (1) and (2) A 0
is the hypocentral source amplitude,
ri
is the distance between the ith station and the seismic source, a is the frequency-dependent attenuation coefficient, f is the frequency of the signal of interest, β is the shear wave velocity, Q is the quality factor for attenuation and n is 0.5 for surface waves and 1 for body waves. In Eqn (1) the
![]() term represents the decrease in amplitude due to geometrical spreading and
term represents the decrease in amplitude due to geometrical spreading and
![]() is the energy loss due to anelastic attenuation (Reference Aki and RichardsAki and Richards, 2002).
is the energy loss due to anelastic attenuation (Reference Aki and RichardsAki and Richards, 2002).
In order to use this approach to locate seismic events, recorded amplitudes must be corrected for specific site effects, such as changes in the material on which the geophone has been deployed (e.g. different rock type, consolidated or unconsolidated sediment). This correction is particularly important in the calving glacier case, where the seismometers are not usually installed on the ice (e.g. Reference O’Neel and PfefferO’Neel and Pfeffer, 2007; Reference O’Neel, Marshall, McNamara and PfefferO’Neel and others, 2007). Reference Battaglia and AkiBattaglia and Aki (2003) calculated coda amplification factors to correct for the site effects, while Reference YamasatoYamasato (1997) calculated site amplification factors by locating known sources.
Following Reference Battaglia and AkiBattaglia and Aki (2003), a two-step approach is used to localize the event hypocentre. First, we perform an extensive search over the range of parameters of interest, (x, y, z, A 0) for body waves and (x, y, A 0) for surface waves. The search region is discretized into a regular set of gridpoints with an interval of Δx, Δy, Δz, ΔA0. At each gridpoint, the least-squares misfit between the measured amplitudes and amplitudes modelled using Eqn (1) is calculated. The grid search allows us to explore the complete model space, reducing the chances of falling into a local minimum. The ten gridpoints with the minimum misfit are stored and used as the initial starting parameters in stage two. The second stage of the procedure is the refinement of the hypocentre using an iteratively damped least-squares method (Reference MoréMoré, 1978), where the point with the minimum misfit is deemed the event hypocentre. For the best-fitting model, the percentage error is defined as (Reference Battaglia and AkiBattaglia and Aki, 2003)
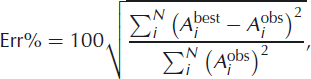
where
![]() and
and
![]() are the observed and best-fitting model amplitudes recorded at each station. The percentage error allows the quantification of the quality of the inversion; a correctly fitting source will have a low percentage error.
are the observed and best-fitting model amplitudes recorded at each station. The percentage error allows the quantification of the quality of the inversion; a correctly fitting source will have a low percentage error.
Field Site
A network of passive seismometers was deployed around a supraglacial lake 70 km from the margin of land-terminating Russell Glacier, West Greenland (67.01° N, 48.74° W), between 27 June and 8 September 2010 (Fig. 1). The ice thickness at the site, estimated from seismic reflection work, is ∼1 km (Reference Booth, Clark, Kulessa, Murray and HubbardBooth and others, 2012). The passive seismic network consisted of six GS-11D velocity geophones with a natural frequency of 4.5 Hz and a bandwidth of ∼5– 1000 Hz, continuously recording microseismic velocities at a sampling rate of 1 kHz on a RefTek-130 digitizer with an aperture of ∼2 km. To improve coupling, the geophones were mounted onto concrete slabs, buried to a depth of ∼0.5 m and routinely reset and buried before they melted out, every 3–5 days. The passive seismic network was designed to image seismic activity associated with the potential reactivation of a closed moulin and healed crevasse running through the lake. The asymmetry of the network, especially to the west and north, reflects the difficulty in accessing these areas, due to a large number of inlet streams to the supraglacial lake and poor conditions underfoot.
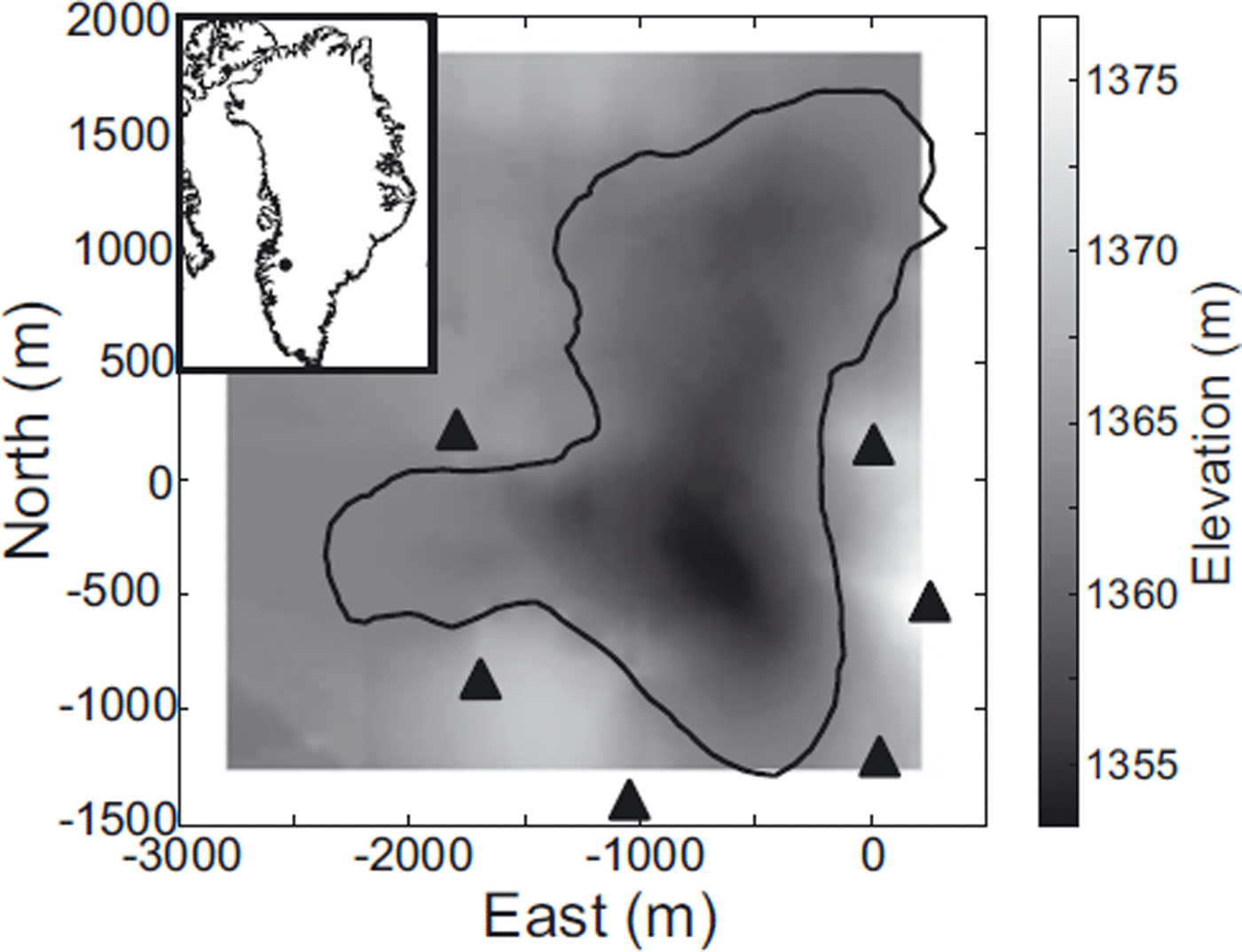
Fig. 1. Location of the field site on Russell Glacier, West Greenland (inset), and the seismic network deployed (black triangles) around a supraglacial lake (black outline). The background shows the surface elevation.
Inspection of the recorded seismicity indicates an extremely seismically active setting. The recorded waveforms show a large degree of variability in the onset of the incoming seismic event, the duration of coda, wave type (i.e. body or surface waves) and frequency content. Inspection of the spectra of recorded seismicity indicates a dominant frequency of 25 Hz, with the frequency spectra falling rapidly after 50 Hz. We associate signals that have frequencies greater than 50 Hz with surface crevassing, due to their impulsive onsets and short time durations (Reference Neave and SavageNeave and Savage, 1970). Further analysis of the seismic events in the <50 Hz frequency band indicates that both body and surface waves were present. We therefore calibrate two models for the location of surface and body waves.
Test Dataset
Model calibration
A seismic reflection experiment was conducted on 3 and 4 July 2010, to gain insight into the material properties at the bed of the ice sheet (Reference Booth, Clark, Kulessa, Murray and HubbardBooth and others, 2012). Five seismic sources, each consisting of 250g of pentalite charge, were drilled to 3 m depth and left overnight to freeze in. The locations of the shots were surveyed before firing, using a Leica SR520 GPS receiver, and processed against an off-ice base station to provide decimetre accuracy. These shots serve as a known source point to calibrate the forward model for values of α in Eqn (1).
The reflection seismic shots were bandpass-filtered using a two-pass Butterworth filter in the frequency range 5–50Hz. To remove any spurious noise spikes we calculate the envelope function of the filtered seismogram as
![]() where
Sn
(t) is the seismogram and
where
Sn
(t) is the seismogram and
![]() is the Hilbert transform of Sn(t) (Reference KanasewichKanasewich, 1981). The root-mean-squared (RMS) amplitudes of the filtered envelope signals were calculated using a 3 s time window with the origin time of the seismic shot occurring at 0.5 s. The 3 s interval was selected so that model parameters could be tested against the complete reflection seismic waveform and would include direct, reflected and surface waves. The length of the time window, and inclusion of the various wave types in the RMS calculation, were selected to be representative of a time window recorded during a seismic swarm.
is the Hilbert transform of Sn(t) (Reference KanasewichKanasewich, 1981). The root-mean-squared (RMS) amplitudes of the filtered envelope signals were calculated using a 3 s time window with the origin time of the seismic shot occurring at 0.5 s. The 3 s interval was selected so that model parameters could be tested against the complete reflection seismic waveform and would include direct, reflected and surface waves. The length of the time window, and inclusion of the various wave types in the RMS calculation, were selected to be representative of a time window recorded during a seismic swarm.
Each of the five shots was fit in a least-squares sense, using both the body and surface wave versions of Eqn (1), with A0 and α as the unknowns. No site effect correction was required, as the RMS amplitude decayed smoothly as a function of hypocentral distance (Fig. 2) and the geophones were deployed in similar conditions on the ice surface. Using the dominant frequency of 25 Hz and the mean value of α from the five seismic shots, Q is estimated at 5 0±6 and 3 5±4 for body and surface waves, respectively. These values of Q are consistent with those estimated from seismic reflection experiments (e.g. Reference SmithSmith, 2007).
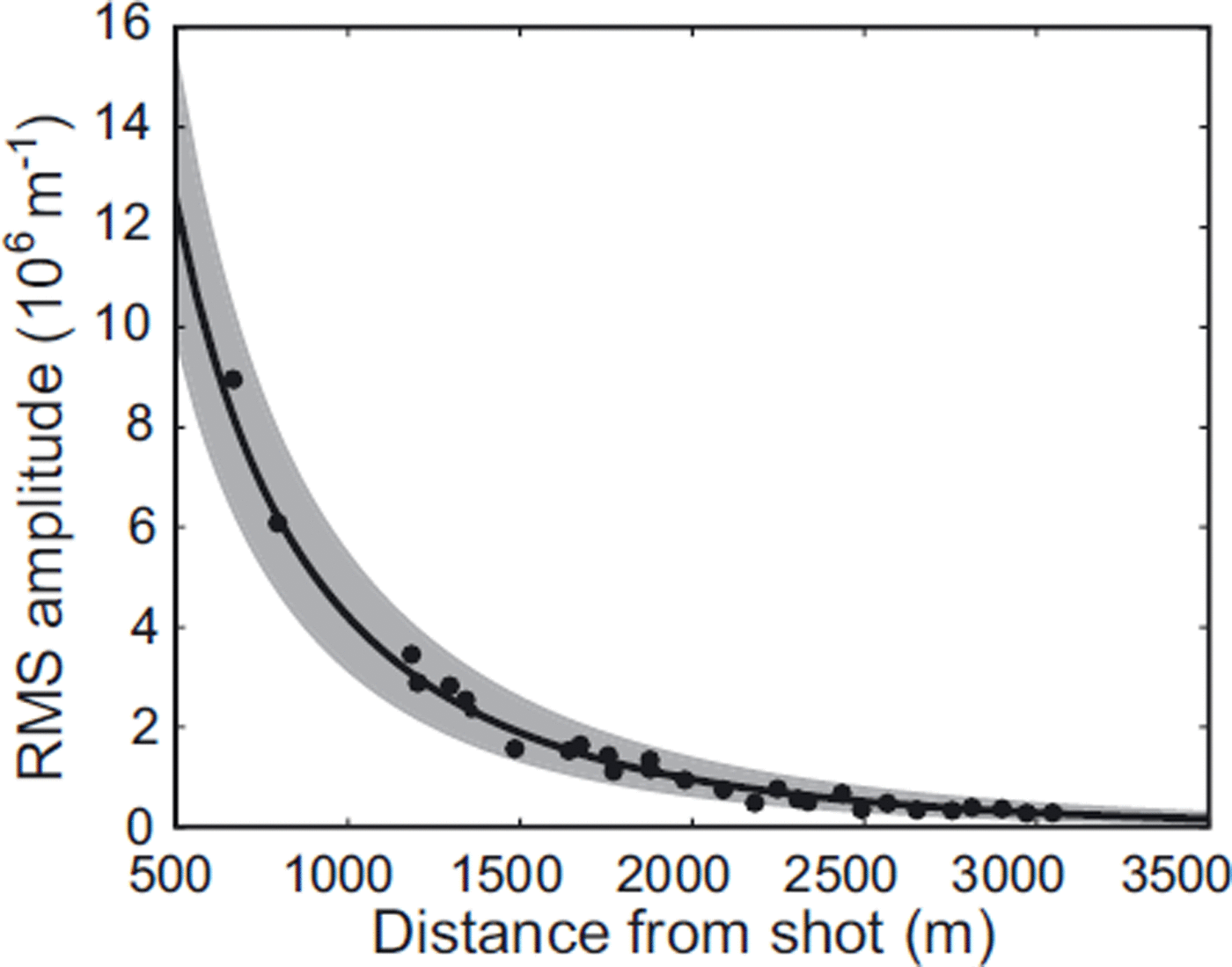
Fig. 2. Measured and modelled RMS amplitudes from seismic reflection shots using a body wave model, where n = 1 in Eqn (1). The black dots are the measured RMS amplitudes, the black curve is the modelled amplitude decay using the mean value of α and the grey-shaded area is the 1σ error bound.
Location of reflection seismic shots
We assess the spatial quality of the five seismic sources by using the mean of the individual values of α as input into the forward model (Eqn (1)). For the initial location of the events using both surface and body wave models, we define a grid x ∊ [-1500,500] m, y [-100,1800] m, and A 0 ∊ [6000,12000] μms–1, with z ∊ [0,1500] m additionally included for the body wave inversion. The resolution of the grid search is set as (Δx, Δy,Δz) of 25 m and ΔA0 of 100 μms–1. The size of the grid was selected to image as much of the lake as possible and the grid spacing was selected to allow the precise determination of the event location while keeping computational time to a minimum.
A summary of the known and estimated locations of the seismic shots is given in Table 1 and Figure 3. Both location methods produce good agreement with the seismic shots. The locations are well constrained in the east direction while in the north direction the errors are twice as large. The poorer results in the north direction may be attributed to the shots being outside the array and having no station coverage in the northern region to constrain the solution. The percentage error in A0 is similar for both body and surface wave inversion (Table 1). Finally, the error estimate in depth is low (mean value of 49 m) and largely well constrained. The body wave inversion produces the best spatial solution, while the surface wave inversion produces the best estimate of source amplitude.
Table 1. Mean error between the known seismic source locations and estimated locations and signal amplitudes from the inversion, using both surface and body wave models
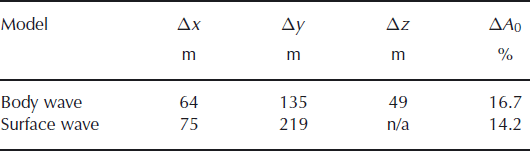
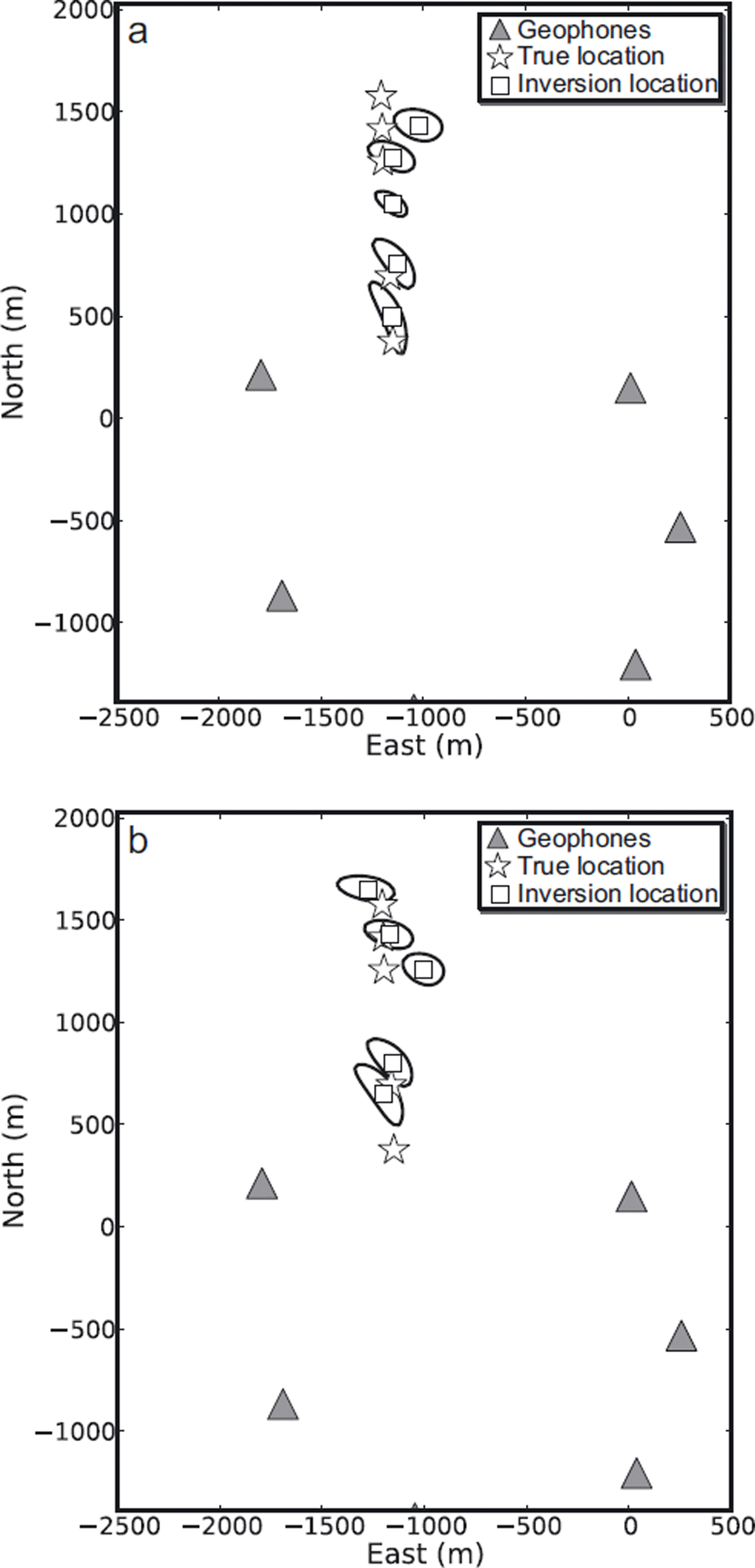
Fig. 3. Map view of the location of the seismic reflection shots (stars) with associated 10% error contour and the inverted events (squares) using a mean α for (a) body and (b) surface wave models.
Figure 4 shows a representative example of a successfully located event, including the event percentage error contours calculated using Eqn (3) and the true location using the body wave inversion. In map view, the error contours close to the solution are elliptically shaped with little smearing, suggesting that the solutions are well constrained. The elliptical nature of the 10% and 20% error surfaces also suggests that the errors close to the true solution are Gaussian. There is significant smearing in the 40% and 50% contours towards the geophones on the west. However, the resolution of the event locations with depth is poorly constrained, due to a trade-off between source amplitude and depth. Overall, the event location is well constrained where the true source points lie within the 20% error bounds, even with sparse station coverage.
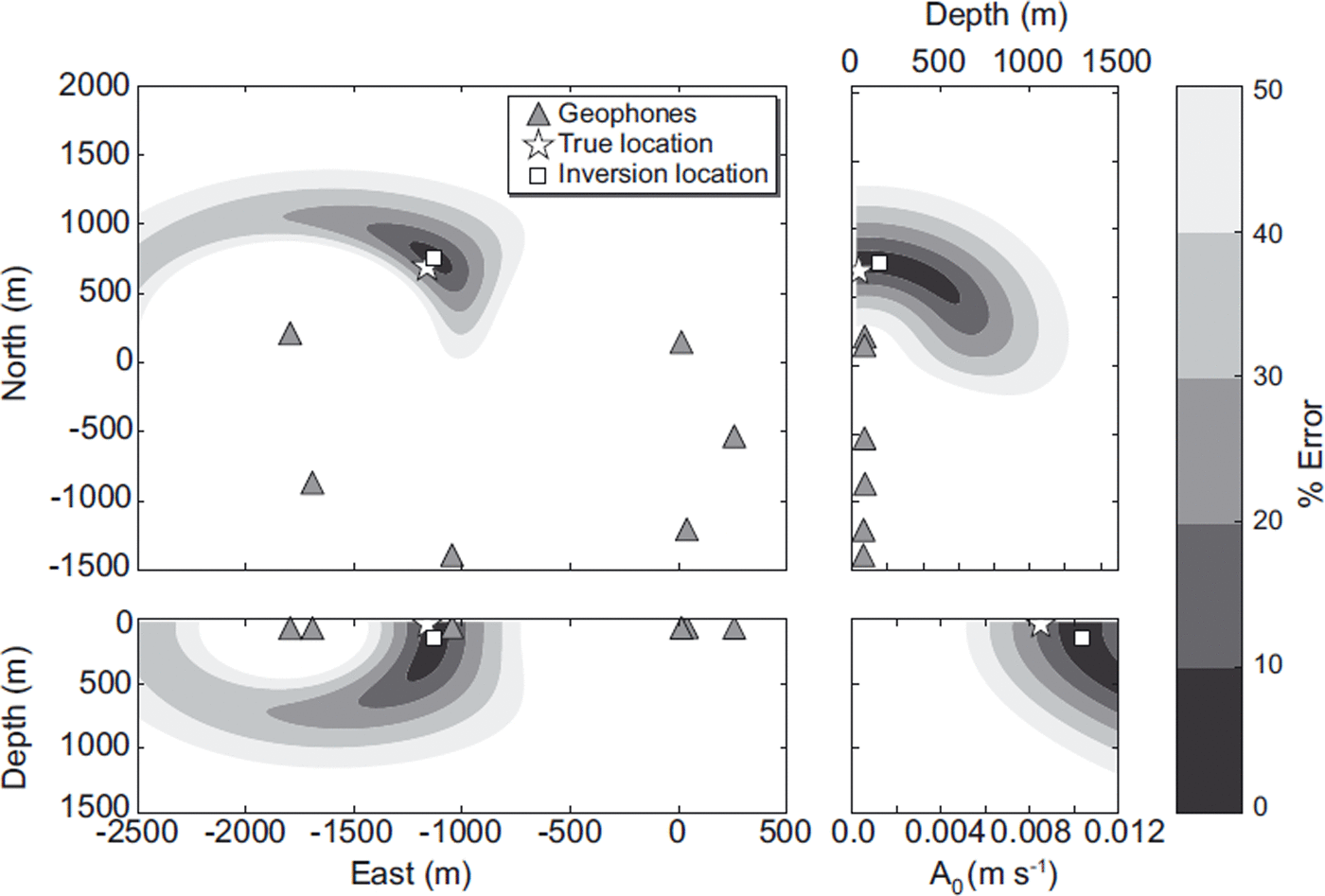
Fig. 4. Application of the body wave inversion to the location of seismic reflection shots. The true source position is shown by the white star, the inversion location is the white square and the geophones are the grey triangles. The percentage error (calculated using Eqn (3)) contours are shown. There is a clear distortion in the >40% error contours, associated with the asymmetry of the shot locations with the geophone network. However, at low percentage error contours, the solution is well constrained in map view, while the depth estimates suffer from a trade-off with source amplitude.
Influence of noise
Following Reference Chambers, Kendall, Brandsberg-Dahl and RuedaChambers and others (2010), we use ‘real’ ambient noise, which is often non-stationary and correlated across the network, to simulate the effect that varying degrees of signal-to-noise ratios (SNR) have on the location of the seismic shot. We take the first 3 s of data, when all stations in the network were recording, as a measure of the ambient noise. The noise trace is multiplied by a scaling factor and added to the seismic shot data. The estimate of SNR across the geophone network may be defined as
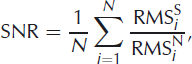
where RMSSi is the pre-processed RMS amplitude of the seismic reflection shot measured using a 3 s window at the ith geophone, RMSN i is the RMS amplitude of the 3 s linebreak noise window after a scaling factor has been applied and N is the total number of geophones.
Figure 5 shows the results of the event location and the error contours for different levels of SNR. In map view there is little change in the location of the seismic shot with varying degrees of SNR. An increase in noise degrades the percentage error contours, thus enhancing the trade-off between A 0 and the source depth. The degradation of the percentage error space is analogous to the deterioration and resolution of the stacked amplitude images used in migration-based location procedures (Reference Chambers, Kendall, Brandsberg-Dahl and RuedaChambers and others, 2010).
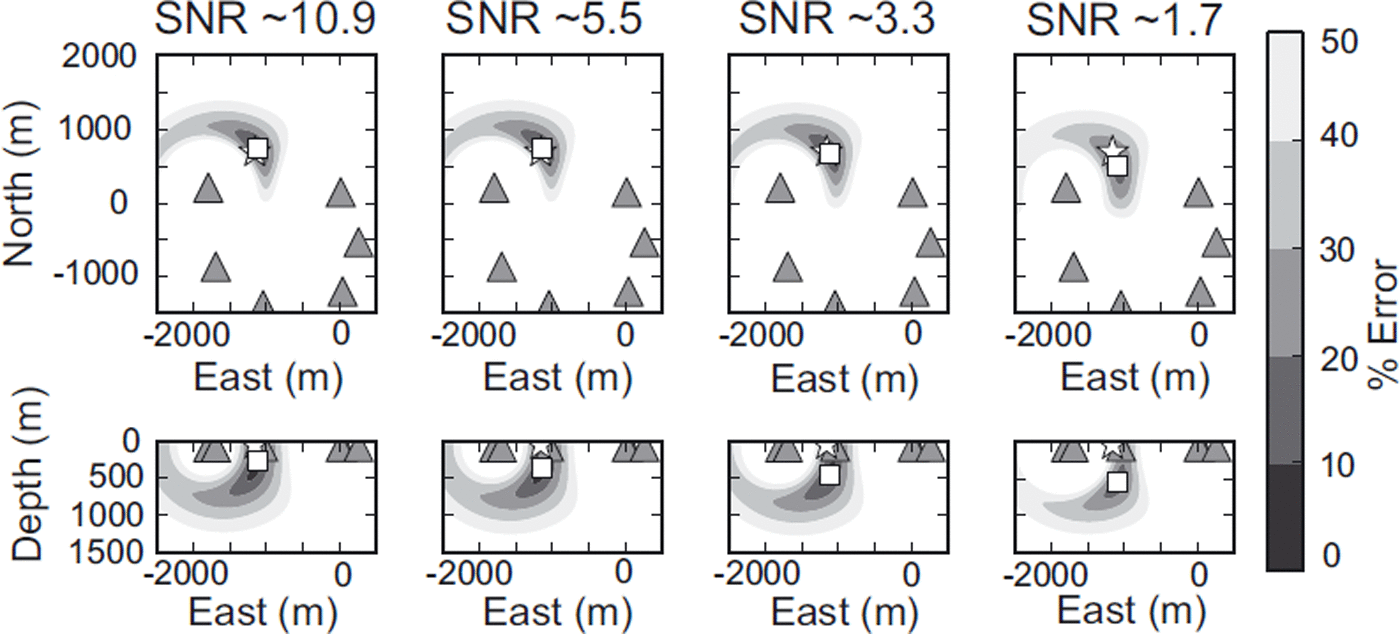
Fig. 5. The effect of varying degrees of SNR on the location of a seismic reflection shot. The true source position is shown by the white star, the inversion location is the white square and the geophones are the grey triangles. The percentage error contours are shown, calculated using Eqn (3). Note the degradation in the error space with decreasing SNR enhancing the trade-off between A 0 and source depth. Increasing the SNR has little effect on the source location in map view.
Resolution and Synthetic Testing
Having accurately located reflection seismic shots using both surface and body wave inversions with a time window with representative seismic phases (e.g. first arrivals, reflected and surface waves), we now focus on the ability of the method to image a synthetic fault plane that is representative of a crevasse associated with the rapid drainage of supraglacial lakes (Reference DasDas and others, 2008). In practice, such data would be processed using similar methods applied to dyke propagation, where the RMS amplitude of the seismic signal is estimated within a time window, which is moved through the seismic swarm (Reference Taisne, Brenguie, Shapiro and FerrazziniTaisne and others, 2011). An inherent assumption of the dyke processing method is that the seismic emissions originate at the propagating fracture tip, resulting in a single isotropic source composed of multiple randomly orientated events (Reference Taisne, Brenguie, Shapiro and FerrazziniTaisne and others, 2011). Here, we test and assess the ability of the amplitude decay location method to accurately locate and image the synthetic fault plane with uncertainties in the value of Q and differing SNR using a Monte Carlo analysis.
The synthetic model was set up based on the network geometry of the Greenland 2010 experiment. The synthetic fault plane follows a mapped east–west trending crevasse from the surface to a depth of 1000 m (Fig. 6), which is the approximate ice thickness. Based on an assumption that the seismicity is isotropic, 200 synthetic events were generated using Eqn (1), with 20 evenly spaced events defining the fault at each 100 m depth interval.

Fig. 6. Median distance location errors for each synthetic seismic event located in the Q uncertainty Monte Carlo sensitivity test. The crosses are the location of the synthetic events, with the colour representing the median error, and the grey triangles are the geophone locations.
Uncertainty in Q
For each synthetic event, we perform a Monte Carlo analysis where the RMS amplitude is calculated using Eqn (1), with the value of Q randomly selected from a Gaussian distribution with a mean of 50 and standard deviation of 6. These values for the Gaussian distribution were selected based on the estimates of Q = 50 ± 6 obtained from the reflection seismic shots discussed earlier (Fig. 2). For each synthetic event, 100 independent perturbations of α were calculated. Figure 6 shows the median distance error between each of the true source locations and the location estimated in the Monte Carlo test. The errors range between 100 and 1000 m and are generally low for the majority of events (<250 m). The largest errors are seen at depth on the eastern side of the fracture and at the surface close to the westernmost geophone.
Figure 7 shows the spatial distribution of the synthetic events located in the Monte Carlo test. The event locations are very well constrained in map view at all depths, with the greatest amount of scatter occurring outside the network to the west and on the far eastern side of the fracture. The events to the west of the array also have a large amount of scatter with depth and do not allow the grid structure of the original synthetic fault plane to be recovered (Fig. 6). The synthetic events at the centre of the array are well constrained in all three directions and allow the original grid structure of the fault plane to be imaged. The events on the eastern side of the fault plane tend to have poor resolution with depth, with a number of events accumulating at the top of the model, leading to the greatest median distance location error (Fig. 6). The poor results for the events on the eastern side of the fault may be attributed to the close proximity of one of the geophones to the fault plane, where small changes in the measured amplitudes dominate the solution through the exponent term (Eqn (1)). From the Monte Carlo analysis the events are well constrained in map view, with an interquartile error range of Δx = 92 m, Δy = 25 m, while the errors in depth have an interquartile range of Δz = 278 m (Fig. 7).
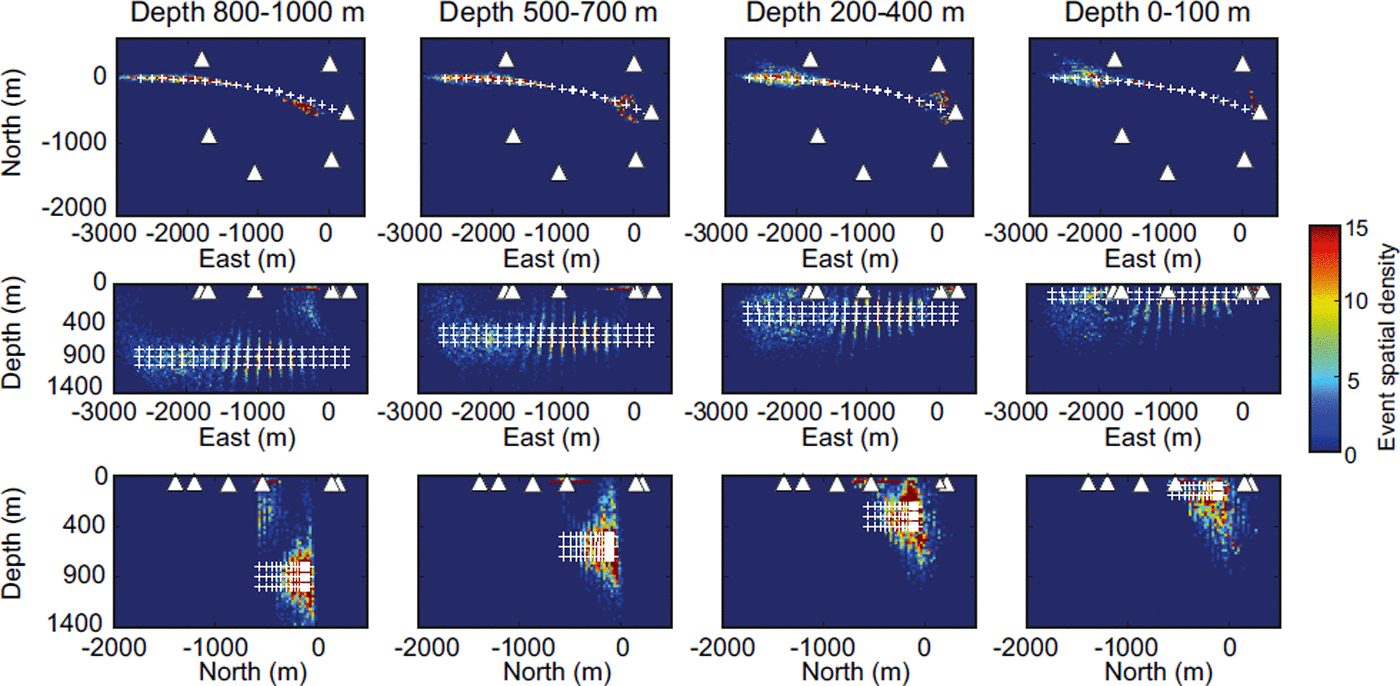
Fig. 7. Spatial density plots of synthetic seismic events located in the Q uncertainty Monte Carlo sensitivity analysis. The spatial density is calculated by binning events into 25 m × 25 m grids. The columns show the spatial density of events at different depth ranges. The white triangles are the geophone locations and the white crosses are the true location of the synthetic seismic events. Note that events on the eastern side of the fracture (-1000 to 0 m) accumulate at the top of the model.
Noise contamination
The second Monte Carlo test assesses the ability of the location procedure to image the fracture plane in the presence of varying degrees of noise. For each location we calculate the RMS amplitude with a constant Q, of 50, using Eqn (1) before adding varying amounts of noise. The noise corresponds to the RMS amplitude of the 3 s of ‘real’ noise, used previously, which is multiplied by a random number selected from a Gaussian distribution to give a mean and standard deviation SNR of 0 and 10, respectively. For each synthetic event, 100 independent perturbations of the noise were calculated and added to the data. Figure 8 shows the median distance error between the true locations and those estimated in the Monte Carlo test. The distribution of the error is similar to that seen in Figure 7, with the error again ranging between 100 and 1000 m, but being, on the whole, low for the majority of events at the centre of the network (<250 m). Once again, the greatest error is seen on the southeastern side of the fracture.

Fig. 8. Median distance location errors for each synthetic seismic event located in the SNR Monte Carlo sensitivity test. The crosses are the location of the synthetic events, with the colour representing the median error, and the grey triangles are the geophone locations.
Figure 9 shows the spatial distribution of synthetic events located in this test. On the whole, the events are well constrained in map view, and (similarly to Fig. 7) the greatest amount of scattering is in locations to the west and outside the network. Events on the western side of the network also show a large degree of scatter with depth and do not allow the grid structure of the original fracture plane to be recovered (Fig. 9). Those synthetic events at the centre of the network are generally well constrained in map view and allow the grid structure of the fault plane to be imaged. Similarly to Figure 5, we notice that the addition of noise tends to cause the seismic events to locate deeper due to the degradation of the error space. Events to the eastern side of the network again suffer from poor depth resolution, with a number of events accumulating at the top of the model. In map view we also observe that the deepest events locate in a circular-like feature around one of the geophones, again highlighting the dominance that the amplitudes measured at that station have on the solution through the exponent term (Eqn (1)). From this analysis, the errors are similar to those obtained in the Q uncertainty test, with interquartile error ranges Δx = 144 m, Δy = 34m and Δz = 271 m (Fig. 9).

Fig. 9. Spatial density plots of synthetic seismic events located in the SNR Monte Carlo analysis. The spatial density is calculated by binning events into 25 m ×25 m grids. The columns show the spatial density of events at different depth ranges. The white triangles are the geophone locations, and the white crosses are the true location of the synthetic seismic events.
Discussion and Conclusions
In the past decade, there has been an increase in the use of passive seismic methods to investigate fracturing in ice masses (e.g. Reference SmithSmith, 2006; Reference BassisBassis and others, 2007; Reference Roux, Marsan, Metaxian, O’Brien and MoreauRoux and others, 2008; Reference Walter, Deichmann and FunkWalter and others, 2008; Reference Winberry, Anandakrishnan and AlleyWinberry and others, 2009; Reference West, Larsen, Truffer, O’Neel and LeBlancWest and others, 2010). Fundamental to these studies is the accurate location of icequakes, both spatially and temporally. We have presented an automated approach that does not require arrival-time picking for the location of icequake swarms, using the decay of the amplitude of the seismic source with distance. The advantage of this method over previous approaches is in the elimination of the requirement to pick and identify seismic phases, which is often difficult and impractical. We tested the method to locate five seismic reflection shots, using a network of six geophones located around a supraglacial lake in West Greenland. Time windows in which the amplitudes of the signal are calculated include direct, reflected and surface waves, in order to be as representative as possible of the data encountered during these swarms. Both a body and a surface wave model were used to locate the seismic shots. The events were accurately located to within 200 m of the true location (Fig. 3), with the largest error occurring in the north direction, which is attributed to a lack of station coverage to the north to constrain the solution. Inspection of the percentage error contours shows that the 10% and 20% contours are elliptically shaped, suggesting the errors close to the true solution are Gaussian. However, there is significant distortion in the 40% and 50% contours towards the west, due to the closer proximity of the seismic shot to a geophone on this side of the lake, which dominates the solution at these gridpoints. Although depth location estimates are in good agreement with the true location (±49 m), inspection of the error space shows a strong trade-off between the source depth and amplitude (Fig. 4). Similar trade-offs are seen in both the traditional arrival-time and migration-based location procedures between the source depth and event origin time in the absence of later phase information (e.g. shear waves; Reference Lee and StewartLee and Stewart, 1981; Reference Chambers, Kendall, Brandsberg-Dahl and RuedaChambers and others, 2010). However, in general, the event locations are well constrained, with the true source position lying within the 20% error bounds, even with sparse station coverage.
A potential source of error in the location procedure is a decrease in the SNR of our data. A single reflection seismic shot was taken and various amounts of ‘real’ ambient noise added to simulate the effect varying degrees of SNR have on the location. In map view there was little change in the location with decreasing SNR. However, the increase in noise levels maps into the percentage error space, thus deteriorating the well-defined error contours and enhancing the trade-off between A 0 and the source depth.
Finally, we tested the resolution of the method to image crevassing driven by hydraulic fracturing, using a model simulating supraglacial lake drainage in Greenland. Two Monte Carlo tests were used to assess the recoverability of the synthetic fracture and associated event location error. The first test examined the effect of an incorrect value of Q on the locations. In general, the synthetic seismic events are well constrained in map view and we were able to recover the grid structure of the synthetic fault plane within the array, with interquartile range error estimates of Δx = 92 m, Δy = 25m and Δz = 278 m. The second Monte Carlo test assessed the influence that varying degrees of noise in the synthetic data would have on the recovered image. The general distribution and magnitudes of the location errors were similar to those obtained in the Q uncertainty analysis (Δx =144 m, Δy = 34 m and Δz = 271 m). We note again that the proximity of the seismic events to one of the geophones leads to the greatest error, with a number of the events accumulating at the top of the model. We attribute this to the proximity of the events to the geophone whose RMS amplitude dominates the solution. The geometry of the seismic network with respect to the seismic source therefore plays an important role in the accuracy and associated error of the located event. The error ranges in both tests were similar to those obtained for the seismic shot locations (Table 1), suggesting that uncertainty in the attenuation parameter, α, and noise levels play an equally significant role in obtaining accurate event locations. The mean horizontal and vertical errors (121 m and 275 m) obtained in this study are similar to those obtained using other migration methods (e.g. Reference Chambers, Kendall, Brandsberg-Dahl and RuedaChambers and others (2010) obtained horizontal errors of 25 m and 152 m). However, we note that a downfall of the method presented here is that it is unable to accurately locate simultaneous distinct sources of seismicity of similar magnitude, due to a degradation of the error space (Reference Battaglia, Aki and FerrazziniBattaglia and others, 2005, their appendix A). Although two or more sources of seismicity may be present during the drainage of a supraglacial lake (e.g. different fracturing events and water drainage), their effects are expected to be short-lived, i.e. a matter of minutes over the 1–2 hours of drainage (Reference DasDas and others, 2008).
In this study we have presented a simple and robust method for the location of icequakes encountered during hydraulically driven fracturing in ice masses. The method is ideally suited to a sparse network of stations, often encountered in glaciological studies. We envisage this method will allow seismicity associated with hydraulic fracturing, such as at calving fronts and the rapid drainage of supraglacial lakes, to be tracked and imaged in both time and space. In both cases, it will provide much-needed data to validate the theory of hydraulic fracturing in ice masses as a method of propagating a fracture from the ice surface to the bed (e.g. Reference Van der VeenVan der Veen, 1998, Reference Van der Veen2007; Reference Tsai and RiceTsai and Rice, 2010). Specifically, for the rapid drainage of supraglacial lakes, the location of the seismicity will serve as a method of directly observing the water accessing the base of the glacier.
Acknowledgements
G.A.J. is supported by UK Natural Environment Research Council (NERC) research grant NE/G007195/1; S.H.D. is supported by an Aberystwyth University doctoral scholarship and C.F.D. is supported by a NERC doctoral scholarship. The Climate Change Consortium of Wales (C3W) is thanked for financial support. The fieldwork was funded by NERC research grants NE/G007195/1 and NE/G005796/1 and the Greenland Analogue Project, Sub-Project A. The seismic instruments were provided by SEIS-UK at the University of Leicester. The facilities of SEIS-UK are supported by NERC under Agreement No. R8/H10/64. The ObsPy library (Reference Beyreuther, Barsch, Krischer, Megies, Behr and WassermannBeyreuther and others, 2010) was used for signal processing of the seismic data. We thank Sridhar Anandakrishnan for providing the shot boxes for firing the seismic shots; Adam Booth, Alessio Gusmeroli and Christian Helanow for help in the field, and Kit Chambers for helpful discussions on the location method. We also thank two anonymous reviewers for constructive comments.












