1. Introduction

Ice-sheet modelling and studies on ice-sheet dynamics carried out so far have been based on Glen’s flow law:

(1)

where is the strain-rate tensor, τ _e is the effective shear stress. σ′ _ij is the deviatoric stress tensor, Q is the activation energy for creep, k is the Boltzmann constant, T is the absolute temperature and n is a constant around 3. Most ice-sheet modellers have used this flow law in their calculations, assuming that the pre-exponential factor A ₀ depends on fabric, impurity concentration, etc. but not on coordinate-system orientation. This assumption, however, is not realistic. Since individual ice crystals have a very strong plastic anisotropy, A ₀ does depend on coordinate-system orientation, if the polycrystalline ice has a preferred c-axis orientation fabric. Glen’s flow law (Equation (1)) can be applied for only isotropic polycrystalline ice which has random c-axis orientation fabric. It is not applicable to an ice sheet in which a preferred orientation of c axes is developing.

Preferred c-axis orientation fabrics generally develop in ice sheets. This fabric development is explained by the c-axis rotation due to basal-glide deformation (Azuma and Higashi, 1985; Alley, 1988; Azuma, 1994) and by recrystallization (Budd and Jacka, 1989; Alley, 1992; Van der Veen and Whillans, 1994). Especially in a deep zone in an ice sheet or at the margin of an ice stream, very strong preferred c-axis orientation fabrics such as a single maximum develop. To explain the flow properties of such characteristic fabric ice, it is necessary to derive a new flow law which takes the flow anisotropy induced by different orientations of individual ice crystals into account. In an experimental study on the deformation behaviour of individual crystals under uniaxial stress, we found the relationships among the c-axis orientation, strain and stress for individual grains (Azuma, 1995). Based on this result, a new flow law for polycrystalline ice in the principal-axes coordinate system was derived (Azuma, 1994).

In this paper, we modify this flow law for the x–y–z coordinate system to be used more conveniently in ice-sheet modelling. We also present the enhancement factors for different deformation patterns, for the case of a single-maximum fabric and that of a small-circle girdle fabric so that modellers can use them in their calculations. Finally, we demonstrate that in a deeper part of an ice sheet, where a single-maximum fabric develops, unique deformation patterns could be produced, depending on the mean orientation of the c axes. This paper is concerned with the effects of the fabric on the constitutive law of stress but it does not touch upon its evolution.

2. A New Flow Law of Ice

We take x, y and z as the coordinates corresponding to the horizontal flow direction, the transverse direction and the vertical upward direction, respectively. Now consider the stresses which deform the ice crystals. We assume that the individual crystals in a polycrystalline aggregate deform only by basal glide. The total resultant stress vector p_(g) acting on the basal plane of an individual grain is determined as follows:

(2)

where σ _(g) is the stress tensor acting on an individual grain and c_(g) is the unit vector parallel to the c axis of the grain. The subscript (g) designates an individual grain. Therefore, the shear stress τ _(g) in the glide direction m_(g) on the basal plane is given by

(3)

Now define a second-order tensor

(4)

where ⊗ denotes the tensor product: 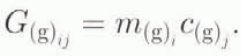. Then, with Equations (3) and (4)

(5)

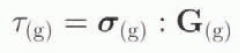
where the double dot product σ _(g): G_(g) denotes 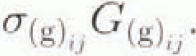. (We shall use Einstein’s summation convention except where explicitly indicated.)

With the following assumptions, we determine the strain-rate components in each grain-coordinate system and convert them to the strain-rate components in the macroscopic x–y–z coordinate system.

Assumptions

(1) Individual grains deform only by basal glide.

(2) The basal glide of each grain takes place in the maximum shear-stress direction on the basal plane when the macroscopic stresses act on the grain.

In an earlier study (Azuma, 1994), the glide direction of each grain was assumed to be the closest direction to the macroscopic maximum shear-stress direction in the aggregate. In this study, to simplify the calculation in the x–y–z coordinates, we assumed the above glide direction. This glide direction gives the minimum total deformation energy and seems to give more realistic deformation of polycrystalline ice than the earlier assumption.

(3) The stress components acting on an individual grain and those on the aggregate are macroscopically related as follows:

(6)

is the local geometric tensor and N _L is the total number of grains in the local area (L) which includes the nearest neighbour grains of the grain and the grain itself. σ _ij is a macroscopic stress tensor acting on the aggregate. Equation (6) means that a larger stress acts on a grain surrounded by softly oriented grains than that surrounded by stiffly oriented grains and a larger stress acts on the stiffer grain. Equation (6) was originally derived empirically for the case of uniaxial compression (Azuma, 1994, 1995). Here, we generalize the empirical equation to an arbitrary macroscopic stress condition.

(4) Shear-strain rate _(g) and shear stress τ _(g) on basal planes of single ice crystals are related by the following power-law equation (Weertman, 1983):

(7)

where β ₀ is a constant, possibly dependent on impurity concentration and other variables but independent of stress configuration.

(5) The macroscopic strain-rate component of the aggregate _ij is equal to the averaged value of the strain-rate components of individual grains :

(8)

where N _T is the total number of grains in the aggregate. Note, in particular, the difference between the two averages 〈〉 and 《 》. Equation (8) was originally derived empirically for the case of uniaxial compression (Azuma, 1994, 1995). Here, we generalize the empirical equation to an arbitrary macroscopic stress condition.

With these assumptions, we now derive a flow law for anisotropic polycrystalline ice in the x–y–z coordinate system in ice sheets.

The unit vector m_(g) in the basal-glide direction can be determined by assumption (2) as follows:

(9)

(10)

(11)

where T_(g) is a tentative resultant stress on the basal plane if the macroscopic stress σ acts on the grain. n_(g) is the unit vector normal to a plane on which three vectors m_(g), c_(g) and T_(g) lie. The unit vector m_(g) can be determined with the stress tensor σ and the unit vector c_(g). Hence, the G factor tensor can be calculated with the c-axis fabric data and the stress condition.

With assumption (3) (Equation (6)), Equation (5) is expressed as follows:

(12)

where we defined τ _(L) as the local shear stress. With assumption (4), Equations (7) and (12), the shear-strain rate on the basal plane in the direction of m_(g) is given as follows:

(13)

where we defined _(L) as the local shear-strain rate. This result (Equation (13)), which was brought about by assumption (3), indicates that the shear-strain rates on the basal plane of individual grains depends on the anisotropy of local regions surrounding the grains rather than the orientations of the grains themselves.

Assumption (1) states that

(14)

where is the component of[]_(g) in a grain-coordinate system e′₁ (= c), e′₂(= m), e′₃. The components in a macroscopic coordinate system e₁, e₂, e₃ are given by

(15)

where e′ _i = a _ij e _j and hence a _pq = e′_p • e_q. Thus,

(16)

Define

(17)

Then, more generally

(18)

With Equation (6), the local strain-rate tensor is expressed as

(19)

For a polycrystalline aggregate, we can substitute, as the first-order approximation, G for G_(L) and hence τ for τ _(L). We then obtain the following flow law of ice.

(20)

where, for the case of reference, we repeat earlier definitions as follows

(21)

Although we showed the stress tensor σ in Equation (20), we could also use the deviatoric stress tensor σ′ instead of σ, as G _xx + G _yy + G _zz = 0. This new flow law (Equations (20) and (21)) demonstrates the direction-dependent mechanical properties of anisotropic ice, as will now be described in the following sections.

Fig. 1. Typical patterns of a single-maximum fabric (a) and a small-circle girdle fabric (b). The centre of each circle corresponds to the vertical axis. The angle ϕ for the single maximum shows the standard deviation of the zenith angles of c axes. For the small-circle girdle pattern, the c axes are distributed so that the zenith angle of each c axis should be ϕ ± 5°.

3. Flow Properties of Characteristic Fabric ICE

At depth in an ice sheet, a single maximum or a small-circle girdle pattern generally develops, depending on the depth and on the stress configuration. The ice with these characteristic fabric patterns deforms in a different manner from that of isotropic ice. For example, the single-maximum fabric ice deforms eight times faster under simple shear, which is perpendicular to the mean c-axis direction, than isotropic ice (Budd and Jacka, 1989). Shoji and Langway (1988) also found experimentally that the Dye 3 ice core, which has a strong single-maximum fabric, deforms easily under horizontal shear but with difficulty under vertical compression. These direction-dependent mechanical properties of anisotropic ice can never be explained by Glen’s flow law (Equation (1)). Below we demonstrate that these can be described well by the above anisotropic flow law (Equations (20) and (21)).

Figure I shows the typical fabric patterns for a single maximum and a small-circle girdle. For these typical fabrics, we calculate the flow-enhancement factors, where the enhancement factor is defined as the ratio of the strain rate for a given anisotropic ice to that for isotropic ice, obtained by this flow law with random (artificial) c-axis orientation distributions. In the case of the single maximum, the c axes are distributed as the Gaussian distribution about the pole. The angle ϕ for a single maximum shows the standard deviation of the zenith angles of c axes. For a small-circle girdle pattern, the c axes are distributed so that the zenith angle of each c axis should be ϕ ± 5°. For each artificial c-axis distribution, which has 1000 c axes, the G tensor was calculated by Equations (20), (21), (9), (10) and (11) for a given stress field σ. Then, the strain-rate tensor was calculated for each. For example, when uniaxial compression and simple shear act on random fabric ice, the stress tensor and the G tensor become Uniaxial compression

Simple shear

Results are shown in Figure 2. The enhancement factor of the horizontal shear deformation for a single maximum (HS(SM)) increases to a value of about 8 as the angle ϕ decreases. On the other hand, the enhancement factor of the vertical compression for a single maximum (VC(SM)) decreases to zero as the angle ϕ decreases. In the case of a small-circle girdle, the enhancement factor for the vertical compression (VC(SCG)) approaches a value of 5 as ϕ approaches 45° and decreases to zero as ϕ moves away from it. These theoretical calculations by the new flow law agree well with the experimental results stated above (Budd and Jacka, 1989).

Fig. 2. Calculated flow-enhancement factors by the present flow law. HS(SM) indicates the enhancement factor for horizontal shear deformation of a single-maximum fabric ice. VC(SM) designates the enhancement factor for the vertical compression of a single-maximum fabric ice. VC(SCG) is that for the vertical compression of a small-circle girdle.

4. Flow Enhancement of DYE 3 ICE

If the stress components and the c-axis orientation fabric at a given depth in an ice sheet are known, the strain-rate components there can he calculated by this flow law (Equation (20)). Dye 3 ice-core fabric data (Herron and others, 1985; Langway and others, 1988) and the borehole survey work (Hansen and Gundestrup, 1988) provide us with good data to examine this flow law. Figure 3 shows the enhancement factors of the Dye 3 ice core calculated theoretically from its fabric data by Equation (20). Solid circles designate the enhancement factors for horizontal shear and open circles show those for vertical compression. Although the vertical strain rates were not measured, the horizontal strain-rate enhancement factor of Dye 3 ice, obtained from the borehole survey, indicates that Wisconsin ice below 1786 m is three limes softer than Holocene ice (Dahl-Jensen and Gundestrup, 1987). This is in good agreement with the present theoretical calculation as shown in Figure 3. This fact supports the applicability of the new flow law (Equation (20)) for ice-sheet flow. This figure also predicts that the enhancement factors for Wisconsin ice are very small for vertical compression. In other words, Wisconsin ice is very hard for vertical compression.

5. Vertical Strain Rate of Deep ICE

As the magnitude of vertical c-axis alignment increases (i.e. as the angle ϕ decreases) the vertical strain-rate enhancement factor decreases as shown in Figure 2. This means that ice with a strong single-maximum fabric like Dye 3 Wisconsin ice cannot deform easily under vertical compression as shown in Figure 3.

Let us calculate the vertical strain-rate profile of Dye 3 with the present anisotropic flow law. We take the x, y and z axes as the flow direction, the transverse direction and the upward direction, respectively. We assume plane-strain conditions, that is, the y component of the strain tensor is zero. We also assume that σ _xy and σ _xy are zero. Hence, the stress tensor and G tensor are expressed as:

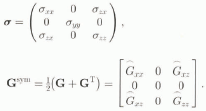
Fig. 3. The flow-enhancement factor of ice from the Dye 3 ice core calculated by the present flow law using observed fabric data. Solid circles designate the enhancement factors for the horizontal shear and open circles show those for vertical compression.

Fig. 4. Calculated stress components and the vertical strain-rate profiles at Dye 3. The horizontal shear-strain rate _zx and the shear stress σ_zx in the flow direction at each depth are known from the borehole survey and the surface-inclination data (Dahl-Jensen and Gundestrup, 1987).

The horizontal shear-strain rate _zx (= 0.5 du/dz) and the vertical strain rate _zz (= dw/dz) are given as follows, where u. and w denote the horizontal (x direction) and the vertical (z direction) flow velocity at a given depth. Thus, Equation (20) implies

(22)

(23)

The horizontal shear-strain rate _zx and the shear stress σ _zx in the flow direction at each depth are known from the borehole survey and the surface inclination data (Dahl-Jensen and Gundestrup, 1987). We assume the artificial c-axis orientation fabric at each depth as follows: ϕ = 80° at 0–1000 m, ϕ = 50°at 1000–1786 m. ϕ = 10° at 1786–2036 m. These are similar to the observed fabric development at Dye 3. With this data set and assumptions, we can determine a plausible solution of σ _xx, σ _yy and σ _zz at each depth so as to satisfy Equation (22). Then dw/dz was calculated from Equation (23). The results are shown in Figure 4. This calculation shows that the vertical strain rate drastically decreases below 1786 m because the c axes almost align vertically. In this calculation, it is found that no combinations of σ _xx , σ _yy and σ _zz satisfy the jump of du/dz at 1786 m, if the c-axis verticality does not increase suddenly from ϕ = 50° to ϕ = 10° at this depth. This fact indicates that only a sudden change in fabric could cause the jump in du/dz.

According to the isotropic flow law (Glen’s flow law), horizontal shear stress itself never produces a vertical strain. Vertical strain is caused by vertical deviatoric stress σ′ _zz . However, in fact anisotropic ice, like single-maximum fabric ice, should produce vertical strain alone with horizontal shear stress. Figure 5 illustrates this feature. If the mean orientation of c axes (i.e. the pole of a single maximum) is inclined with respect to the vertical axis, normal strain components (ε _xx and ε _zz ) are produced by horizontal shear stress. The anisotropic flow law (Equation (20)) can demonstrate this characteristic flow property of anisotropic ice. We discuss this more quantitatively below.

Figure 6 shows the ratio of the vertical strain rate to the horizontal shear-strain rate which is calculated by Equation (20), by assuming that only horizontal shear stress acts on the ice body. The ratio is shown against the standard deviation of the zenith angles of c axes (ϕ) for each inclination angle λ of the mean orientation of c axes (MOC). The positive angle λ means that the MOC inclines towards downstream. This result clearly indicates that, if the MOC inclines towards upstream, the horizontal shear in the ice sheet produces positive vertical strain. This means that, if the annual layer is horizontal, the annual layer thickness increases with time due to the shear ice flow.

Fig. 5. Anisotropic ice flow at a deeper part of an ice sheet. If the mean orientation of c axes is inclined towards upstream or downstream, even the horizontal shear stress atone produces vertical strain.

Fig. 6. The ratio of the vertical strain rate to the horizontal shear-strain rate which is calculated by the present flow law, assuming that only a horizontal shear stress acts on an ice body. The ratio is shewn against the standard deviation of the angles between c axes and a pole of single maximum (ϕ) with the tilled angle λ. A positive angle λ means that the mean direction of c axes inclines towards downstream. A negative angle λ means that the mean direction of c axes inclines towards upstream.

For Dye 3 Wisconsin ice, we estimated the vertical strain rate for the inclined MOC with respect to the flow direction. Figure 7 shows one example for 1800 m depth. In ice sheets the real stress field is complicated. To simplify, we assume a plane-strain condition as above. To satisfy this condition for a single-maximum fabric ice like Dye 3 Wisconsin ice, the present flow law requires a uniaxial stress (σ′ _xx = −2σ′ _yy = −2σ′ _zz ) in addition to the shear stress σ _zx . as can be seen in Figure 4. For three different inclination angles of MOC (λ = 0°, 5° and −5°), the horizontal shear-strain rate du/dz and the vertical strain rate du/dz were calculated for various values of σ′ _xx . From Figure 7 it is found that positive vertical strain rates of the order of 10⁻³ a⁻¹ are produced if λ = −5°, while negative vertical strain rates of the order of 10⁻³ a⁻¹ are produced when λ = 5°. This means that the inclination angle of MOC is very important for describing the vertical flow of deep ice. Detailed ice-fabric studies on Dye 3 Wisconsin ice reveal that the MOC inclines about 5–15° from the core axis, depending on depth (Langway and others, 1988). Although the core axis is not vertical and inclines at most 6° near the bottom, the mean direction of c axes definitely inclines several degrees from the vertical axis. Unfortunately, due to lack of information on the geographical orientation of the Dye 3 core, the vertical strain of Wisconsin ice cannot be discussed in detail.

Fig. 7. Vertical strain rate dw/dz and horizontal shear-strain rate dw/dz (calculated by the present flow law) versus σ′_xx at Dye 3 1800 m depth. Results for three different inclination angles λ of the MOC are given: 0°, 5° and −5°.

At depth, the MOC varies slightly in the horizontal and the vertical directions. If the MOC varies in the vertical direction (fig. 8a), the layers with positive λ become thinner with time while the layers with negative λ become thicker with time by horizontal shear. This suggests a heterogeneous layer thinning. If the MOC varies in the horizontal direction (Fig. 8b), even initially horizontal layers could produce layer folding or boudinage.

Fig. 8. Expected characteristic deformation of annual layers caused by the spatial variation of the MOC. If the MOC varies vertically (a), both layer thinning and thickening can occur depending on the direction of the MOC. If the MOC varies horizontally (a), layer folding or boudinage could occur.

6. Conclusions

The generalized flow law (Equation (1)), which has been used in all ice-flow calculations, is not appropriate for studies of ice-sheet dynamics because the polycrystalline ice in ice sheets has a strong plastic anisotropy caused by a preferred c-axis orientation. In this paper, a new flow law for anisotropic ice observed in the deeper parts of ice sheets has been derived. This flow law is simply expressed with the strain-rate tensor, the stress tensor and the geometric factor tensor (G), which is determined by using the c-axis fabric data and the stress condition. This flow law can describe well the direction-dependent mechanical properties of anisotropic ice which can never be explained by Glen’s flow law. The flow-enhancement factors for anisotropic ice calculated by this flow law agree well with the experimental results and field observations. We also show that anisotropic ice in the deeper parts of ice sheets deforms in a manner different from isotropic ice. This may significantly affect flow-model dating of an ice core and the ice-sheet dynamics.