Introduction
Biological processes of milk synthesis in the mammary gland have been studied extensively and modelled (Neal and Thornley, Reference Neal and Thornley1983; Dijkstra et al., Reference Dijkstra, France, Dhanoa, Maas, Hanigan, Rook and Beever1997; Vetharaniam et al., Reference Vetharaniam, Davis, Upsdell, Kolver and Pleasants2003b). Yields of milk in dairy cattle and other species are largely a function of the number of mammary secretory cells and the secretory activity per cell (Knight, Reference Knight1989 and Reference Knight2000; Dijkstra et al., Reference Dijkstra, France, Dhanoa, Maas, Hanigan, Rook and Beever1997; Capuco et al., Reference Capuco, Wood, Baldwin, Mcleod and Paape2001). The numbers of active secretory mammary cells at different stages of the lactation are determined by the balance between the rates of proliferation and quiescence into non-secretory cells (Molenaar et al., Reference Molenaar, Davis and Wilkins1992; Knight, Reference Knight2000). Proliferation, the process where undifferentiated mammary cells progress to an active secretory state, occurs at an exponential rate from the start of gestation and reaches a maximum soon after parturition when mammary cell numbers are at their peak (Knight, Reference Knight and Wilde1993). Shortly after parturition, a proportion of mammary cells progress to a quiescent or resting pool of non-secretory mammary cells. These quiescent cells can either be reactivated to milk-secreting mammary cells, or they can proceed to senescence which is often termed apoptosis (Molenaar et al., Reference Molenaar, Davis and Wilkins1992; Wilde et al., Reference Wilde, Quarrie, Tonner, Flint and Peaker1997).
The effects of nutrition, or feeding level, genetic merit, levels of body fat or age on each process of the mammary gland are not clear. Nutritional changes affect circulating levels in blood of glucose, a major precursor of milk, to the mammary gland (Pollott, Reference Pollott2004). Knight (Reference Knight2000) showed the amount of mammary tissue was directly proportional to milk yields in cows of low or high genetic merit. Similar results were obtained in a study of Jersey cattle by Davis et al. (Reference Davis, Hughson, Bryant and Mackenzie1985). Broster and Broster (Reference Broster and Broster1998) reported that higher body condition scores (BCS), in the range of thin to moderate levels, generally resulted in elevated milk yields in early lactation, but they concluded the benefits of higher BCS are unclear for later lactation. Age affects milk yields, with lower potential milk yields in younger animals (Nielsen et al., Reference Nielsen, Friggens, Lovendahl, Jensen and Ingvartsen2003), which may be partially due to lower live weights in younger animals. For example, Linzell (Reference Linzell1972) presented results within and amongst species which illustrated that both milk yield and mammary gland weight were positively correlated with live weight. Although these results illustrate the effects of nutrition, genetic merit, body fatness and age on total or daily yields, they do not provide a quantitative framework with which the effect of each factor can be simulated in a model of the mammary gland.
Vetharaniam et al. (Reference Vetharaniam, Davis, Upsdell, Kolver and Pleasants2003b) constructed a model that simulated milk synthesis in the mammary gland by linking the effects of nutrition and genotype. Using a small data set of two Holstein Friesian genotypes managed on diets of pasture or total mixed ration, they found the estimated active population of alveoli, or milk-secreting mammary cells, throughout lactation was related to actual yields. The objectives of the present study were to utilise data from a New Zealand trial to further quantify the effects of nutrition, genetic merit, body fatness and age on the parameters in the model of the mammary gland constructed previously by Vetharaniam et al. (Reference Vetharaniam, Davis, Soboleva, Shorten and Wake2003a and Reference Vetharaniam, Davis, Upsdell, Kolver and Pleasantsb).
Material and methods
Mammary gland model
The objective of this section is to give a brief introduction of the mammary gland model of Vetharaniam et al. (Reference Vetharaniam, Davis, Soboleva, Shorten and Wake2003a and Reference Vetharaniam, Davis, Upsdell, Kolver and Pleasantsb). Key equations and an adapted schematic (Figure 1) are reproduced below:
In brief, the mammary gland model consists of alveoli (groups of secretory cells) in various states of activation or inactivation (Figure 1). At the start of lactation each animal has an initial pool of active alveoli, A 0. The number of active alveoli, A t (equation 14) at time t is dependent on a series of equations (equations 1 to 13) with the initial condition (t = 0) where A t = A 0. The rate of production of active alveoli by progenitor (undifferentiated) cells, r pa, decays exponentially throughout the lactation with an initial constant, k 1, and decay constant, k 2 (equation 1). Throughout lactation, active alveoli can proceed to a state of quiescence (non-secretory cells) with the size of the quiescent pool defined in equation 15. The rate of quiescence of active alveoli, r aq, is proportional to A t and k 3 (equation 2). The quiescent alveoli then become either, reactivated to secretory alveoli (secretory cells) or proceed to senescence. The rate of reactivation of quiescent alveoli, r qa, is proportional to the quiescent alveoli population and a constant k 4 (equation 3). The rate of senescence of quiescent alveoli, r qs, is proportional to the number of quiescent alveoli and k 5 (equation 4). The total production of alveoli from conception until the end of lactation, A produced, is: A 0+k 1/k 2. At any stage of the lactation, milk energy output (I; equation 17) is influenced by the relative energy status of the animal (E; equation 16), which is a ratio of actual feed intake (FI a) versus theoretical maximum feed intake (FI max), the number of active alveoli (A t), a theoretical maximum secretion rate (S; 3 × 10− 9 MJ/day based on previous data) and a nutritional response factor (L) which is invoked when E is less than 1.00.

Figure 1 Schematic diagram of the mammary gland model (adapted with permission based on Vetharaniam et al. (Reference Vetharaniam, Davis, Soboleva, Shorten and Wake2003a)). Abbreviations: A t = active secretory alveoli at time t, Q = quiescent alveoli, S = secretion rate per active alveoli, r pa = rate of differentiation from progenitor to active secretory alveoli, r aq = rate at which active secretory alveoli proceed to quiescence, r qa = rate at which quiescent alveoli are reactivated to become active secretory alveoli, and r qs = rate at which quiescent alveoli proceed to senescence.
Animal data
To quantify the effects of level of feeding, genetic merit, BCS, and age on the biological parameters of the described mammary gland model, a data set was obtained from a New Zealand trial with Jersey cattle in the 1999/2000 season. Data consisted of an initial estimate of BCS around parturition and then up to 15 (herd tests carried out at 14-day intervals) measurements of daily yields of milk, fat and protein per cow per lactation, and corresponding days in milk at each test. Total lactation yields of milk, fat and protein, live weight at peak lactation (22 October), days in milk and estimates of breeding values (EBV) for milk for each individual animal were also obtained. Estimates of intakes of pasture and supplements at each test were calculated from the area grazed per cow daily, pre- and post-grazing masses of pasture and supplements offered.
The Jersey cows were managed at different feeding levels: high, medium, low and very low. The corresponding estimates of average feed intakes for each feeding level group over the lactation period were 13.47, 13.02, 12.40 and 11.74 kg dry matter (DM) per cow per day, respectively. Initially, 40 cows were assigned to each feeding level group. Little supplement was fed, and was generally high-quality pasture silage fed to all feeding level groups at rates of 2 to 3 kg DM per cow per day for approximately 4 weeks at the start and end of the lactation. The relative energy status, E, at each herd test was determined based on estimated intakes of pasture and supplements of each feeding level group divided by theoretical maximum intakes of 16 kg DM per cow per day (approx. 4% of live weight). The energy value per kg of milk was calculated from milk yields, and fat, protein and lactose component concentrations based on the equations of Dado et al. (Reference Dado, Mertens and Shook1993).
Evolutionary algorithm analyses
To determine estimates of model parameters, A o, k 1, k 2, k 3, k 4, k 5, L and A produced, for the milk yield lactation curve of each individual animal, an evolutionary algorithm add-in for Microsoft Excel© called Genetic Algorithm (YearStretch, 2005) was applied to the system of equations outlined by Vetharaniam et al. (Reference Vetharaniam, Davis, Upsdell, Kolver and Pleasants2003b). Evolutionary algorithms have proved efficient at finding the global optima in a number of agricultural models (Mayer et al., Reference Mayer, Belward and Burrage1996; Hart et al., Reference Hart, Larcombe, Sherlock and Smith1998). Evolutionary algorithms are based on the biological concepts of reproduction where two selected individuals, with different genetic codes, are ‘mated’ or crossed to produce the next generation. In the context of the present study, the individuals are an array of estimates of mammary gland model parameters. Over generations, or iterations, the process combines successful parameter values, which improve the fitness of the population. While crossover is the dominant genetic operation, mutation is also introduced at each mating to rediscover any potential beneficial parameter values. Through successive mating of selected individuals (arrays), the population structure tends to find a near-optimal solution (Mayer et al., Reference Mayer, Belward, Widell and Burrage1999).
The parameter bounds specified in Table 1, were based on the estimates obtained by Vetharaniam et al. (Reference Vetharaniam, Davis, Upsdell, Kolver and Pleasants2003b). Fitness was defined as the size of the mean prediction error (MPE) of actual compared with predicted milk yields, the smaller the better as outlined by Fuentes-Pila et al. (Reference Fuentes-Pila, DeLorenzo, Beede, Staples and Holter1996). Mayer et al. (Reference Mayer, Belward and Burrage2001) recommends a population size of approximately twice the dimensionality of the problem, but not too small to ensure genetic diversity. Based on the present seven-dimensional problem, an initial population size of 50 with the 25 best arrays of parameters surviving per iteration seemed reasonable. However, MPE was reduced further when using a population size of 100 with the best 50 selected and was therefore adopted for evolutionary algorithm analyses. Mutation, which was at an automated rate in the Genetic Algorithm add-in, was used to rediscover any potential beneficial parameters values in subsequent iterations. The evolutionary algorithm ran for 50 iterations, and the parameter values that minimised MPE was then kept for each individual animal. Based on these individual parameter values, an estimate of the number of active alveoli was also obtained at peak (A peak) and mid to late (A mid-late) lactation. Peak and mid to late lactation corresponded to the test nearest to day 35 and day 150 after a cow's parturition, respectively. Pearson's correlation coefficients between A o, k 1, k 2, k 3, k 4, k 5, L, A produced, A peak and A mid-late were also calculated to determine the association between estimated mammary gland model parameters.
Table 1 Summary of parameter bounds for the mammary gland model

Multiple regression analyses
To determine the effect of the continuous variables of feeding level (average feed intake), genetic merit (EBVs), BCS, and age (from birth) on total lactation yields of milk, fat and protein, live weight around the time of peak milk yield, days in milk, and the evolutionary algorithm derived mammary gland parameters (A o, k 1, k 2, k 3, k 4, k 5, L, A produced, A peak and A mid-late), the REG procedure in the Statistical Analysis System package, version 8 (SAS, 1999) was used. The multiple regression model was:

where y is the dependent variable, a is the intercept, b 1-b 8 are the regression coefficients for feeding level (FL), genetic merit (GM), BCS and Age as linear and quadratic effects, and e is the residual error. Genetic merit was defined as the deviation in milk EBV relative to the animal in the data set with the lowest milk EBV. For each trait, a backward regression procedure was used where the non-significant (P>0.10) effects were removed from the model. If the intercept was deemed non-significant (P>0.10) it was also removed from the model.
Multicollinearity among multiple regression predictor variables, which can inflate standard errors and parameter estimates, was investigated by obtaining the variance inflation factor calculated as 1/(1 - R 2), where R 2 is the coefficient of determination from ordinary least-squares regression of a predictor variable in relation to all other predictors in the model (Phillipi, Reference Phillipi, Scheiner and Gurevitch1994). Variance inflation factors of 10 or greater were considered to indicate a problem with multicollinearity (Phillipi, Reference Phillipi, Scheiner and Gurevitch1994). This threshold was only exceeded when linear and quadratic terms of an effect were included in the selected model. In the instances where multicollinearity was detected, the ORTHOREG procedure (SAS, 1999), which accounts for multicollinearity by orthogonalising the data using a Gentleman-Givens transformation, was applied to the selected regression model to find unbiased standard errors and parameter estimates (Yu, Reference Yu2000).
Results
Means, standard deviations and model accuracy
The parameter k 5, which influences persistency of milk yields, showed the greatest variability (Table 2). The degree of variability of L, which determines the animal response at times of nutritional stress, was low even though the pre-defined parameter space was 3.0 to 7.0 × 10− 1.The model was able to match predicted and actual milk yield values with a high degree of accuracy (Figures 2 and 3). Accuracy was greatest at the intermediate feeding levels. The threshold of 0.10 error as suggested by Fuentes-Pila et al. (Reference Fuentes-Pila, DeLorenzo, Beede, Staples and Holter1996) where there is a poor fit between actual and predicted values was not exceeded for any animals in the data set.
Table 2 Descriptive statistics for the mammary gland parameters
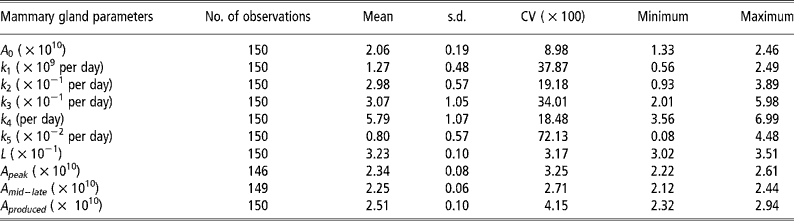

Figure 2 Distribution of mean prediction error (MPE) of predicted v. actual values at high (■), medium (![]() ), low (
), low (![]() ) and very low (
) and very low (![]() ) feeding levels.
) feeding levels.

Figure 3 Example lactation curves of predicted (△) and actual (●) milk yields (a) high feeding level, (b) moderate feeding level, (c) low feeding level, (d) very low feeding level. Abbreviations: MPE = mean prediction error, R 2 = coefficient of determination.
Correlations between mammary gland parameters
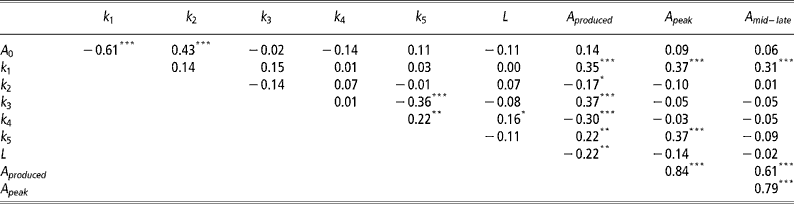
As expected the highest positive correlations (P < 0.001) was observed between A peak and A mid-late (Table 3). Significant negative correlations (P < 0.001) were observed between A 0 and k 1, k 3 and k 5, and k 4 and A produced. Significant positive correlations (P < 0.001) were observed between A 0 and k 2, k 1 with A produced, A peak and A mid–late, k 3 and A produced, and k 5 and A peak.
Table 3 Pearson's correlation coefficients between mammary gland parameters
Feeding level
As expected, greater total lactation yields of milk, fat and protein were observed at higher feeding levels (Table 4). Contributing, to these differences in yields were an increase in lactation lengths at higher feeding levels. The rate, at which new alveoli are produced, largely determined by k 1, was affected by feeding level, with higher production rates at lower feeding levels (Table 5). The rate at which the production of new alveoli declines with time, largely determined by k 2, was highest at intermediate feeding levels. Level of feeding significantly affected the senescence rate of quiescent alveoli, k 5 (higher senescence rate = reduced persistency), with the highest value at a very low feeding level. A produced and A peak were at their maximum value in the low feeding level environment.
Table 4 Significant regression coefficients for feeding level (FL), genetic merit (GM), body condition score (BCS) at parturition and age for milk, fat and protein yield, days in milk and live weight around the time of peak lactation†

† L = linear, Q = quadratic.
‡ Approaching significance (P < 0.1).
Table 5 Significant regression coefficients for feeding level (FL), genetic merit (GM), body condition score (BCS) at parturition and age for parameters of the mammary gland model†

† L = linear, Q = quadratic.
‡ Approaching significance (P < 0.1).
Genetic merit
A scaling effect was observed at high feeding levels with greater gains in milk and fat yields per 1-kg increase in milk EBV observed than at low feeding levels (Table 4). The total production of alveoli from conception until the end of lactation, A produced, also exhibited a genetic merit × feeding level scaling effect. A significant genetic merit × age scaling effect was observed for protein yield and A 0, the initial population of active alveoli at the start of lactation. The senescence of quiescent alveoli, k 5, displayed a significant linear effect for genetic merit with lower senescence rates in animals of superior genetic merit. Genetic merit had a significant linear effect on A peak and A mid-late with more active alveoli in animals of superior genetic merit (Table 5).
Body condition score at parturition
Higher BCS at parturition were associated with reduced total lactation yields of milk and protein (Table 4). As expected, BCS at parturition had a significant positive linear effect on live weight around the time of peak milk yield. A produced, A peak and k 3 were highest at intermediate BCS of 4.0 to 4.5 (Table 5).
Age
Age had significant linear and quadratic effects on total lactation yields with yields increased initially up to approximately 8 years of age and declining thereafter (Table 4). Age also had a significant linear effect on k 1, which influences the rates at which new alveoli are produced, with higher rates in younger animals (Table 5). The reactivation of quiescent alveoli, k 4, exhibited the same general trend as total lactation yields, with an increase initially up to about 6 years of age but declining thereafter. The total number of alveoli produced from conception until the end of lactation, A produced, declined initially as animals' aged reaching its lower asymptote at 5 years of age but rose thereafter.
Discussion
The model was able to fit individual lactation curves that corresponded to actual curves with a high degree of accuracy. This was achieved using information related to the nutritional status of the group of cows at each feeding level rather than for individual animals. While it would have been preferable to have an individual estimate of feed intake for each cow, measured by the n-alkane method or calculated from measurements of milk yield, live weight and live weight changes, this was not possible from available data.
Not unexpectedly, some of the mammary gland parameters were correlated (Table 3). The negative correlation between A 0 and k 1 indicates that if initial mammary gland cell numbers are higher, then the rate of production of active alveoli by progenitor (undifferentiated) cells is depressed and vice versa. The negative correlation between k 3 and k 5 suggests animals with an increased the rate of quiescence of active alveoli (k 3) are also less likely to reactivate quiescent alveoli (k 5). These are probably animals with a high peak, but low levels of persistency. This is further verified through the observed positive correlation between A peak and k 5, with higher k 5 values increasing the rate of senescence of quiescent alveoli. Animals that can reactivate quiescent alveoli need to produce less alveoli throughout lactation, as indicated by the negative correlation between k 4 and A produced. Animals with higher initial alveoli numbers, A 0, are also more likely to have a lower production of active alveoli by progenitor (undifferentiated) cells as mediated through a higher decay constant, k 2. As expected, higher k 1 values, which increase the rate of production of active alveoli by progenitor (undifferentiated) cells, increase A produced and the number of active alveoli in peak and mid-late lactation, A peak and A mid–late, respectively.
The rate at which new alveoli are produced, or cellular proliferation, largely determined by k 1, was affected by level of feeding, with higher values at lower feeding levels. Similarly, Vetharaniam et al. (Reference Vetharaniam, Davis, Upsdell, Kolver and Pleasants2003b) found k 1 was lower on a diet of essentially ad libitum total mixed ration than high intake levels of pasture. As suggested by Vetharaniam et al. (Reference Vetharaniam, Davis, Upsdell, Kolver and Pleasants2003b), it is difficult to explain this result as higher feeding levels or nutrient densities would be expected to increase the proliferation rate of alveoli, as observed by Norgaard et al. (2005). However, it may be that lower levels of feeding prior to parturition in the current study may have suppressed alveoli production and it was not until the animal started lactating that alveoli production was fully activated. Animals on very high feeding levels prior to parturition may have their alveoli population largely fixed at parturition.
Interestingly, A peak was highest at very low feeding levels. However, this did not result in high milk yields in the very low feeding level environment because milk energy output (I) is a function of the number of active alveoli (A t), secretion rate per active alveoli (S), energy status (E) and the nutritional buffer factor (L) (equation 17). Therefore, as E is often below unity in a very low feeding level than in a high feeding level environment, milk yields are suppressed in the former compared with latter environment. In addition, low feeding levels have a negative effect on BCS and based on the results presented in Table 5, this would result in a reduction in A peak.
The senescence rate of quiescent alveoli, k 5, was highest at the very low feeding level. This is consistent with results presented by Knight (Reference Knight2001) for supplemented and un-supplemented cows. However, high k 5 values were also observed at the highest feeding level. No effect of diet or level of feeding on k 4 was found in contrast to the results of Vetharaniam et al. (Reference Vetharaniam, Davis, Upsdell, Kolver and Pleasants2003b). This suggests a diet effect on k 4 may be expressed only when two widely different diets are compared e.g. pasture v. total mixed ration, or wide ranges of feeding levels are imposed.
In the present study, we observed a genetic merit × feeding level scaling effect for total lactation yields of milk and fat and this is consistent with numerous other studies (Veerkamp et al., Reference Veerkamp, Simm and Oldham1994; O'Connell et al., Reference O'Connell, Buckley, Rath and Dillon2000; Kennedy et al., Reference Kennedy, Dillon, Faverdin, Delaby, Buckley and Rath2002). Based on the values presented in Table 4, at feed intakes of 12 and 13 kg DM per cow that correspond to an approximate average of the present study, we would expect for every 1-kg increase in milk EBV that total lactation yields of milk would increase by 1.67 and 1.81 kg, respectively. This is significantly greater than the theoretical expectation of 1 kg milk per 1 kg increase in milk EBV. The scaling effect is possibly due to the overall study environment being superior to the environment which Jersey cows experience in the national herd (Anonymous, 2000). The observed genetic merit × feeding level scaling effect for A produced, provides a potential mechanism by which scaling effects are expressed at a mammary cell level.
In the present study, the total number of alveoli at peak and mid to late lactation (A peak and A mid-late, respectively) increased linearly with genetic merit. Vetharaniam et al. (Reference Vetharaniam, Davis, Upsdell, Kolver and Pleasants2003b) reported that a North American Holstein Friesian genotype had lower values for A t, than a New Zealand Holstein Friesian genotype when they were managed on pasture. Whereas, on a diet of total mixed ration, A t was higher in the North American than New Zealand Holstein Friesian genotype, indicating a re-ranking type of genotype × environment interaction. Similarly, re-ranking between genotypes managed on the different diets was observed for k 3, k 5, and A produced. The re-rankings for the parameters were consistent with the significant re-ranking for milk solids yields (genetic merit) exhibited by the two genotypes when managed on diets of either pasture or total mixed ration (Kolver et al., Reference Kolver, Roche, De Veth, Thorne and Napper2002) but significant only for k 3. Davis et al. (Reference Davis, Hughson, Bryant and Mackenzie1985) found udder volume, theoretically correlated to the population of active alveoli (i.e. A t; see Figure 1), was significantly greater in high than low genetic merit Jersey cattle. In Friesian cattle, udder volume did not differ between low and high genetic merit groups, but secretory output per active alveoli was significantly greater in the high genetic merit group. Based on the results of this study and previous studies, higher genetic merit animals in a particular environment achieve higher yields through greater pools of active alveoli throughout lactation (A t), or increased secretory output per active alveolus, elevated levels of persistency (i.e. flatter lactation curve), and higher levels of total alveoli produced from conception until the end of lactation than low genetic merit animals.
In the present study, increased BCS at parturition resulted in reduced total yields of milk and protein. We also observed that animals at intermediate BCS of 4.0 to 4.5 at parturition had the highest values for A produced and A peak. However, the rates of active alveoli proceeding to quiescence (k 3) were highest at intermediate BCS at parturition. Waltner et al. (Reference Waltner, McNamara and Hillers1993) found total lactation yields were reduced at very high and low BCS compared with intermediate BCS. Heuer et al. (Reference Heuer, Schukken and Dobbelaar1999) and Domecq et al. (Reference Domecq, Skidmore, Lloyd and Kaneene1997) found higher BCS at parturition did not increase total lactation yields or yields to 120 days of lactation, respectively. While, the benefits of higher BCS at parturition on milk yields appear to be minimal, there may be a confounding effect of genetic merit (Waltner et al., Reference Waltner, McNamara and Hillers1993). For example, there is a negative genetic correlation between BCS and milk yields, meaning animals which are genetically fatter, achieve lower milk yields than genetically thin animals (Pryce et al., Reference Pryce, Coffey and Simm2001; Veerkamp et al., Reference Veerkamp, Koenen and De Jong2001; Coffey et al., Reference Coffey, Simm, Oldham, Hill and Brotherstone2004). Due to the confounding effects of genetic merit and the low number of animals in the present study we cannot make any definite conclusions on a BCS at parturition, which will optimise milk yields or the number of active alveoli throughout lactation.
We observed increased yields of fat up to 8 years of age but decreases thereafter. Initial rates of differentiation of progenitor cells, k 1, declined with age. The reactivation of quiescent alveoli, k 4, was greatest in animals of 5 to 8 years of age. The exact mechanisms by which quiescent alveoli are reactivated into secretory alveoli is not certain (Molenaar et al., Reference Molenaar, Davis and Wilkins1992). Reactivation of quiescent alveoli may be lower in two-year-old animals than 5- to 8-year-old animals because the former are often still partitioning energy towards growth i.e. a trade-off mechanism between milk production and growth. The trade-off mechanism, combined with the expected reduction in mammary tissue for animals at lower live weights (Linzell, Reference Linzell1972), could also explain the significantly reduced total lactation yields in two year-old animals. Our results, do not provide compelling evidence to explain the findings of previous empirical studies (Varona et al., Reference Varona, Moreno, Cortes and Altarriba1998; Tozer and Huffaker, Reference Tozer and Huffaker1999), where lactation persistency is reduced in older animals than in 2- and 3-year-old animals.
Knight (Reference Knight2000) and Wilde et al. (Reference Wilde, Quarrie, Tonner, Flint and Peaker1997) state that manipulating mammary cell proliferation and senescence holds potential to modify persistency of milk yields. In the present model, genetics of lactation persistency are expressed in a number of the mammary gland parameters, namely k 2 - k 5 which control the flow of alveoli from states of active secretory to senescence. We observed from our analyses that cows of superior genetic merit exhibited reduced rates of quiescent alveoli proceeding to senescence (k 5). Vetharaniam et al. (Reference Vetharaniam, Davis, Upsdell, Kolver and Pleasants2003b) observed k 5 was lower on a diet of total mixed ration compared with pasture. Therefore, lactation persistency could be enhanced through the use of energy dense diets (i.e. total mixed ration) and superior genotypes. The potential to select genotypes for lactation persistency was illustrated by Muir et al. (Reference Muir, Fatehi and Schaeffer2004), who estimated lactation persistency in first lactation Canadian Holstein Friesians was moderately heritable (h 2 = 0.18).
Conclusion
Overall, the results illustrate the model's potential as a tool to fit a lactation curve and to help in understanding the effects of level of feeding or diet, genetic merit, body condition score and age on the dynamics of milk yields during lactation. The next logical progression is to use the derived mathematical functions to assess their ability to accurately predict milk yields for any cow, at any stage of lactation, based on information related to her nutritional status, genetic merit, body condition score and age. Further, studies could also investigate the effect of specific genes on milk yield and milk composition throughout lactation.
Acknowledgements
The senior author would like to acknowledge the support of an Enterprise Doctoral Scholarship provided jointly by the Livestock Improvement Corporation and the Foundation for Research, Science and Technology. The comments and suggestions of K. Vetharaniam (AgResearch, New Zealand) were greatly appreciated.












