This paper is devoted to the study of some asymptotic behaviors of Poisson-Voronoi tessellation in the Euclidean space as the space dimension tends to ∞. We consider a family of homogeneous Poisson-Voronoi tessellations with constant intensity λ in Euclidean spaces of dimensions n = 1, 2, 3, …. First we use the Blaschke-Petkantschin formula to prove that the variance of the volume of the typical cell tends to 0 exponentially in dimension. It is also shown that the volume of intersection of the typical cell with the co-centered ball of volume u converges in distribution to the constant λ−1(1 − e−λu). Next we consider the linear contact distribution function of the Poisson-Voronoi tessellation and compute the limit when the space dimension goes to ∞. As a by-product, the chord length distribution and the geometric covariogram of the typical cell are obtained in the limit.

Small-world graphs are examples of random graphs which mimic empirically observed features of social networks. We propose an intrinsic definition of small-world graphs, based on a probabilistic formulation of scaling properties of the graph, which does not rely on any particular construction. Our definition is shown to encompass existing models of small-world graphs, proposed by Watts (1999) and studied by Barbour and Reinert (2001), which are based on random perturbations of a regular lattice. We also propose alternative constructions of small-world graphs which are not based on lattices and study their scaling properties.

We build a family of Markov chains on a sphere using distance-based long-range connection probabilities to model the decentralized message-passing problem that has recently gained significant attention in the small-world literature. Starting at an arbitrary source point on the sphere, the expected message delivery time to an arbitrary target on the sphere is characterized by a particular expected hitting time of our Markov chains. We prove that, within this family, there is a unique efficient Markov chain whose expected hitting time is polylogarithmic in the relative size of the sphere. For all other chains, this expected hitting time is at least polynomial. We conclude by defining two structural properties, called scale invariance and steady improvement, of the probability density function of long-range connections and prove that they are sufficient and necessary for efficient decentralized message delivery.

Throughout recent years, various sequential Monte Carlo methods, i.e. particle filters, have been widely applied to various applications involving the evaluation of the generally intractable stochastic discrete-time filter. Although convergence results exist for finite-time intervals, a stronger form of convergence, namely, uniform convergence, is required for bounding the error on an infinite-time interval. In this paper we prove easily verifiable conditions for the filter applications that are sufficient for the uniform convergence of certain particle filters. Essentially, the conditions require the observations to be accurate enough. No mixing or ergodicity conditions are imposed on the signal process.

We study a process where balls are repeatedly thrown into n boxes independently according to some probability distribution p. We start with n balls, and at each step, all balls landing in the same box are fused into a single ball; the process terminates when there is only one ball left (coalescence). Let c := ∑jpj2, the collision probability of two fixed balls. We show that the expected coalescence time is asymptotically 2c−1, under two constraints on p that exclude a thin set of distributions p. One of the constraints is c = o(ln−2n). This ln−2n is shown to be a threshold value: for c = ω(ln−2n), there exists p with c(p) = c such that the expected coalescence time far exceeds c−1. Connections to coalescent processes in population biology and theoretical computer science are discussed.

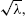We present a method to obtain both exact values and sharp estimates for the total variation distance between binomial and Poisson distributions with the same mean λ. We give a simple efficient algorithm, whose complexity order is to compute exact values. Such an algorithm can be further simplified for moderate sample sizes 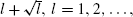n, provided that λ is neither close to from the left nor close to 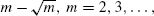from the right. Sharp estimates, better than other known estimates in the literature, are also provided. The 0s of the second Krawtchouk and Charlier polynomials play a fundamental role.

We study sample covariance matrices of the form W = (1 / n)CCT, where C is a k x n matrix with independent and identically distributed (i.i.d.) mean 0 entries. This is a generalization of the so-called Wishart matrices, where the entries of C are i.i.d. standard normal random variables. Such matrices arise in statistics as sample covariance matrices, and the high-dimensional case, when k is large, arises in the analysis of DNA experiments. We investigate the large deviation properties of the largest and smallest eigenvalues of W when either k is fixed and n → ∞ or kn → ∞ with kn = o(n / log log n), in the case where the squares of the i.i.d. entries have finite exponential moments. Previous results, proving almost sure limits of the eigenvalues, require only finite fourth moments. Our most explicit results for large k are for the case where the entries of C are ∓ 1 with equal probability. We relate the large deviation rate functions of the smallest and largest eigenvalues to the rate functions for i.i.d. standard normal entries of C. This case is of particular interest since it is related to the problem of decoding of a signal in a code-division multiple-access (CDMA) system arising in mobile communication systems. In this example, k is the number of users in the system and n is the length of the coding sequence of each of the users. Each user transmits at the same time and uses the same frequency; the codes are used to distinguish the signals of the separate users. The results imply large deviation bounds for the probability of a bit error due to the interference of the various users.

We consider a stochastic fluid queue served by a constant rate server and driven by a process which is the local time of a reflected Lévy process. Such a stochastic system can be used as a model in a priority service system, especially when the time scales involved are fast. The input (local time) in our model is typically (but not necessarily) singular with respect to the Lebesgue measure, a situation which, in view of the nonsmooth or bursty nature of several types of Internet traffic, is nowadays quite realistic. We first discuss how to rigorously construct the (necessarily) unique stationary version of the system under some natural stability conditions. We then consider the distribution of performance steady-state characteristics, namely, the buffer content, the idle period, and the busy period. These derivations are much based on the fact that the inverse of the local time of a Markov process is a Lévy process (a subordinator), hence making the theory of Lévy processes applicable. Another important ingredient in our approach is the use of Palm calculus for stationary random point processes and measures.

Consider a sequence (Xk: k ≥ 0) of regularly varying independent and identically distributed random variables with mean 0 and finite variance. We develop efficient rare-event simulation methodology associated with large deviation probabilities for the random walk (Sn: n ≥ 0). Our techniques are illustrated by examples, including large deviations for the empirical mean and path-dependent events. In particular, we describe two efficient state-dependent importance sampling algorithms for estimating the tail of Sn in a large deviation regime as n ↗ ∞. The first algorithm takes advantage of large deviation approximations that are used to mimic the zero-variance change of measure. The second algorithm uses a parametric family of changes of measure based on mixtures. Lyapunov-type inequalities are used to appropriately select the mixture parameters in order to guarantee bounded relative error (or efficiency) of the estimator. The second example involves a path-dependent event related to a so-called knock-in financial option under heavy-tailed log returns. Again, the importance sampling algorithm is based on a parametric family of mixtures which is selected using Lyapunov bounds. In addition to the theoretical analysis of the algorithms, numerical experiments are provided in order to test their empirical performance.

We investigate the properties of multifractal products of geometric Ornstein-Uhlenbeck (OU) processes driven by Lévy motion. The conditions on the mean, variance, and covariance functions of the resulting cumulative processes are interpreted in terms of the moment generating functions. We consider five cases of infinitely divisible distributions for the background driving Lévy processes, namely, the gamma and variance gamma distributions, the inverse Gaussian and normal inverse Gaussian distributions, and the z-distributions. We establish the corresponding scenarios for the limiting processes, including their Rényi functions and dependence structure.

This paper deals with censoring of infinite-state banded Markov chains. Censoring involves reducing the time spent in states outside a certain set of states to 0 without affecting the number of visits within this set. We show that, if all states are transient, there is, besides the standard censored Markov chain, a nonstandard censored Markov chain which is stochastic. Both the stochastic and the substochastic solutions are found by censoring a sequence of finite transition matrices. If all matrices in the sequence are stochastic, the stochastic solution arises in the limit, whereas the substochastic solution arises if the matrices in the sequence are substochastic. We also show that, if the Markov chain is recurrent, the only solution is the stochastic solution. Censoring is particularly fruitful when applied to quasi-birth-and-death (QBD) processes. It turns out that key matrices in such processes are not unique, a fact that has been observed by several authors. We note that the stochastic solution is important for the analysis of finite queues.

We consider stochastic replicator processes for games that are composed of finitely many trials. Several general results on the relation between Nash equilibria and the long-run behaviour of the stochastic processes are proved. In particular, a sufficient condition is given for almost sure convergence to a state where everyone plays in every trial a strict Nash equilibrium. The results are applied to multiple-trial conflicts based on wars of attrition and on sperm competition games with fair raffles, respectively.

We introduce a modification of the linear ARCH (LARCH) model (Giraitis, Robinson, and Surgailis (2000)) - a special case of Sentana's (1995) quadratic ARCH (QARCH) model - for which the conditional variance is a sum of a positive constant and the square of an inhomogeneous linear combination of past observations. Necessary and sufficient conditions for the existence of a stationary solution with finite variance are obtained. We give conditions under which the stationary solution with infinite fourth moment can exhibit long memory, the leverage effect, and a Lévy-stable limit behavior of partial sums of squares.