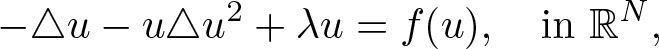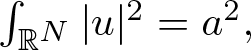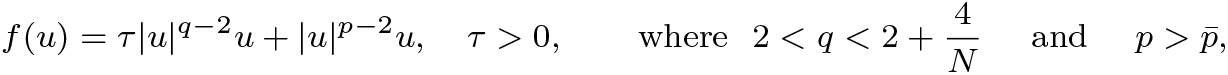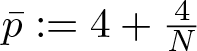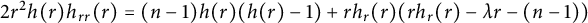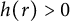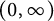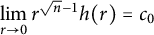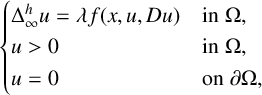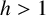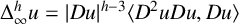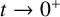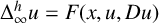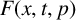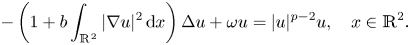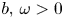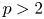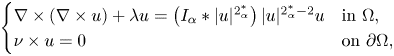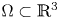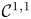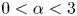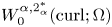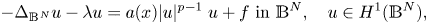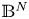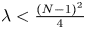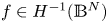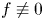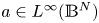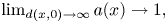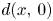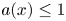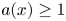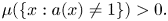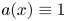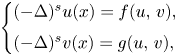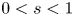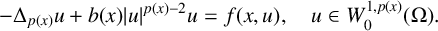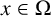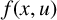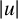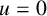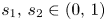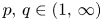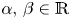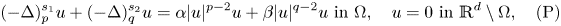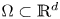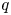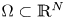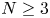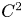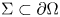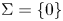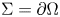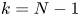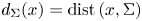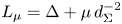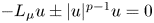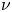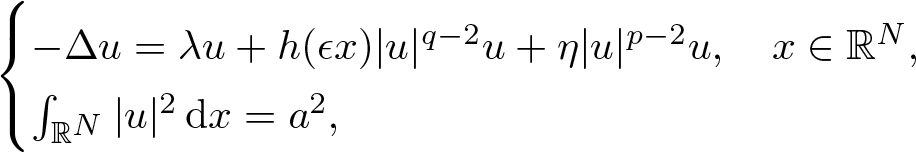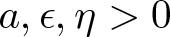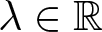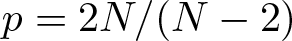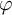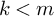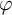357 results in 35Jxx
On the fractional powers of a Schrödinger operator with a Hardy-type potential
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1-48
-
- Article
- Export citation
Normalized solutions to the quasilinear Schrödinger equations with combined nonlinearities
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1-39
-
- Article
- Export citation
Existence of singular rotationally symmetric gradient Ricci solitons in higher dimensions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 21 March 2024, pp. 1-18
-
- Article
- Export citation
VISCOSITY SOLUTIONS TO THE INFINITY LAPLACIAN EQUATION WITH SINGULAR NONLINEAR TERMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 20 March 2024, pp. 1-30
-
- Article
- Export citation
Necessary and sufficient conditions for ground state solutions to planar Kirchhoff-type equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 March 2024, pp. 1-22
-
- Article
- Export citation
A class of Hessian quotient equations in de Sitter space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 06 March 2024, pp. 1-17
-
- Article
- Export citation
On a critical time-harmonic Maxwell equation in nonlocal media
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 February 2024, pp. 1-45
-
- Article
- Export citation
Multiplicity of positive solutions for a class of nonhomogeneous elliptic equations in the hyperbolic space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 February 2024, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Qualitative properties of solutions for system involving the fractional Laplacian
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1-16
-
- Article
- Export citation
On the Γ-convergence of the Allen–Cahn functional with boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 12 February 2024, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the existence of a nodal solution for p-Laplacian equations depending on the gradient
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 31 January 2024, pp. 1-22
-
- Article
- Export citation
MULTIPLE SOLUTIONS FOR
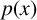 $p(x)$-LAPLACIAN EQUATIONS WITH NONLINEARITY SUBLINEAR AT ZERO
$p(x)$-LAPLACIAN EQUATIONS WITH NONLINEARITY SUBLINEAR AT ZERO
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 29 January 2024, pp. 1-9
-
- Article
- Export citation
On generalized eigenvalue problems of fractional (p, q)-Laplace operator with two parameters
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 January 2024, pp. 1-46
-
- Article
- Export citation
On Calderon's problem for the connection Laplacian
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 05 January 2024, pp. 1-26
-
- Article
- Export citation
Systems involving mean value formulas on trees
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 03 January 2024, pp. 1-33
-
- Article
- Export citation
Semilinear elliptic equations involving power nonlinearities and Hardy potentials with boundary singularities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 21 December 2023, pp. 1-58
-
- Article
- Export citation
Symmetrized and non-symmetrizedasymptotic mean value Laplacian in metric measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1-38
-
- Article
- Export citation
Multiplicity and stability of normalized solutions to non-autonomous Schrödinger equation with mixed non-linearities
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 09 November 2023, pp. 1-27
-
- Article
- Export citation
LELONG NUMBERS OF m-SUBHARMONIC FUNCTIONS ALONG SUBMANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 07 November 2023, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence of renormalized solutions to fully anisotropic and inhomogeneous elliptic problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 31 October 2023, pp. 1-37
-
- Article
- Export citation