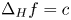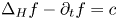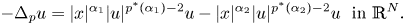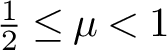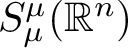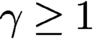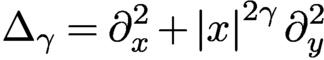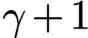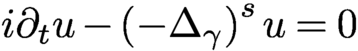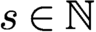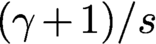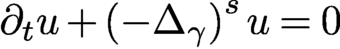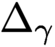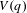13 results in 35Hxx
GLOBAL HYPOELLIPTICITY OF SUMS OF SQUARES ON COMPACT MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 05 January 2024, pp. 1-35
-
- Article
- Export citation
A note on monotonicity and Bochner formulas in Carnot groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 1543-1563
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The ground states of quasilinear Hénon equation with double weighted critical exponents
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 03 June 2022, pp. 1037-1044
- Print publication:
- June 2023
-
- Article
- Export citation
LOG-TRANSFORM AND THE WEAK HARNACK INEQUALITY FOR KINETIC FOKKER-PLANCK EQUATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 16 May 2022, pp. 2749-2774
- Print publication:
- November 2023
-
- Article
- Export citation
SPECTRAL INEQUALITIES FOR COMBINATIONS OF HERMITE FUNCTIONS AND NULL-CONTROLLABILITY FOR EVOLUTION EQUATIONS ENJOYING GELFAND–SHILOV SMOOTHING EFFECTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 21 March 2022, pp. 2533-2582
- Print publication:
- November 2023
-
- Article
- Export citation
Riemannian approximation in Carnot groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 06 September 2021, pp. 1139-1154
- Print publication:
- October 2022
-
- Article
- Export citation
OBSERVABILITY OF BAOUENDI–GRUSHIN-TYPE EQUATIONS THROUGH RESOLVENT ESTIMATES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 14 June 2021, pp. 541-579
- Print publication:
- March 2023
-
- Article
- Export citation
GLOBAL SUBELLIPTIC ESTIMATES FOR KRAMERS–FOKKER–PLANCK OPERATORS WITH SOME CLASS OF POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 22 June 2020, pp. 675-711
- Print publication:
- March 2022
-
- Article
- Export citation
An application of the theorem on Sums to viscosity solutions of degenerate fully nonlinear equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 975-992
- Print publication:
- April 2020
-
- Article
- Export citation
ANALYTIC HYPOELLIPTICITY FOR SUMS OF SQUARES IN THE PRESENCE OF SYMPLECTIC NON TREVES STRATA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1877-1888
- Print publication:
- November 2020
-
- Article
- Export citation
THE UNIQUE CONTINUATION PROPERTY OF
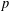 $p$-HARMONIC FUNCTIONS ON THE HEISENBERG GROUP
$p$-HARMONIC FUNCTIONS ON THE HEISENBERG GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 12 November 2018, pp. 219-230
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
A result of multiplicity of solutions for a class of quasilinear equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 291-309
-
- Article
-
- You have access
- Export citation
THE ESSENTIAL SPECTRUM OF A PERTURBED OPERATOR ARISING IN TWO-DIMENSIONAL MAGNETOHYDRODYNAMICS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 16 April 2010, pp. 169-182
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation