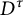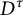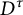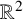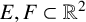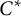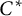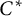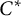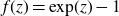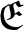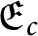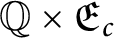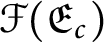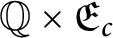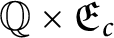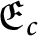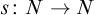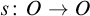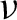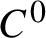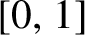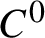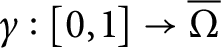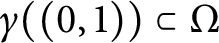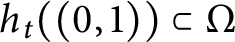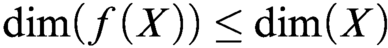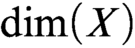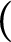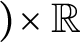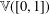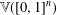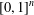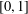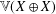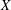46 results in 54Fxx
Sufficient conditions for non-zero entropy of closed relations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 15 February 2024, pp. 1-29
-
- Article
- Export citation
On homogeneity of Cantor cubes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 28 February 2023, pp. 1084-1090
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON ARITHMETIC SUMS OF CONNECTED SETS IN
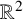 $\mathbb {R}^2$
$\mathbb {R}^2$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 13 January 2023, pp. 507-519
- Print publication:
- June 2023
-
- Article
- Export citation
The generator rank of subhomogeneous
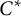 $C^*\!$-algebras
$C^*\!$-algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 14 June 2022, pp. 1314-1342
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Point Degree Spectra of Represented Spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 27 May 2022, e31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distinguishing endpoint sets from Erdős space
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 15 February 2022, pp. 635-646
- Print publication:
- November 2022
-
- Article
- Export citation
A characterization of the product of the rational numbers and complete Erdős space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 27 January 2022, pp. 87-102
- Print publication:
- March 2023
-
- Article
- Export citation
A DEDEKIND-STYLE AXIOMATIZATION AND THE CORRESPONDING UNIVERSAL PROPERTY OF AN ORDINAL NUMBER SYSTEM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 26 January 2022, pp. 1396-1418
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dendrites and measures with discrete spectrum
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 15 December 2021, pp. 545-555
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A characterization of a map whose inverse limit is an arc
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 2533-2549
- Print publication:
- August 2022
-
- Article
- Export citation
THE MCKINSEY–TARSKI THEOREM FOR LOCALLY COMPACT ORDERED SPACES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 29 April 2021, pp. 187-211
- Print publication:
- June 2021
-
- Article
- Export citation
A variational principle for the metric mean dimension of free semigroup actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 01 February 2021, pp. 65-85
- Print publication:
- January 2022
-
- Article
- Export citation
Generic homeomorphisms have full metric mean dimension
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 28 December 2020, pp. 40-64
- Print publication:
- January 2022
-
- Article
- Export citation
The Brouwer invariance theorems in reverse mathematics
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e51
-
- Article
-
- You have access
- Open access
- Export citation
Shortest paths in arbitrary plane domains
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 09 November 2020, pp. 349-367
- Print publication:
- April 2022
-
- Article
- Export citation
Periodic points for amenable group actions on uniquely arcwise connected continua
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 30 September 2020, pp. 2833-2844
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
DIMENSION INEQUALITY FOR A DEFINABLY COMPLETE UNIFORMLY LOCALLY O-MINIMAL STRUCTURE OF THE SECOND KIND
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 07 September 2020, pp. 1654-1663
- Print publication:
- December 2020
-
- Article
- Export citation
On cohesive almost zero-dimensional spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 15 July 2020, pp. 429-441
- Print publication:
- June 2021
-
- Article
- Export citation
THE COMPLEXITY OF HOMEOMORPHISM RELATIONS ON SOME CLASSES OF COMPACTA
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 733-748
- Print publication:
- June 2020
-
- Article
- Export citation
EMBEDDINGS OF FREE TOPOLOGICAL VECTOR SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 20 August 2019, pp. 311-324
- Print publication:
- April 2020
-
- Article
- Export citation