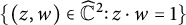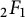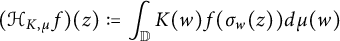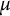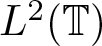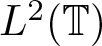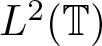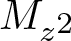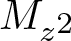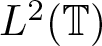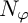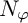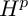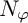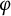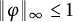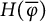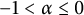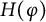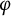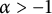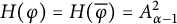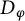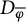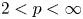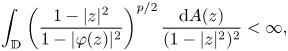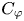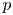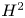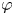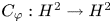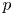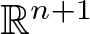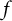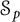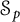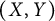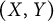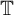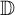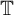81 results in 30Hxx
Phase retrieval on circles and lines
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1-9
-
- Article
-
- You have access
- HTML
- Export citation
Inhomogeneous Poisson processes in the disk and interpolation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 30 April 2024, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random analytic functions with a prescribed growth rate in the unit disk
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 26 April 2024, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sobolev trace-type inequalities via time-space fractional heat equations
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 25 March 2024, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CLASS OF SYMBOLS THAT INDUCE BOUNDED COMPOSITION OPERATORS FOR DIRICHLET-TYPE SPACES ON THE DISC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 14 March 2024, pp. 1-6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral theory of the invariant Laplacian on the disk and the sphere – a complex analysis approach
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 01 March 2024, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hausdorff operators on some classical spaces of analytic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 29 February 2024, pp. 768-780
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Integral mean estimates for univalent and locally univalent harmonic mappings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 15 January 2024, pp. 655-669
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Commutants and complex symmetry of finite Blaschke product multiplication operator in
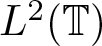 $L^2(\mathbb{T})$
$L^2(\mathbb{T})$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 261-286
-
- Article
-
- You have access
- HTML
- Export citation
On the Extension of Bounded Holomorphic Maps from Gleason Parts of the Maximal Ideal Space of
 $H^\infty $
$H^\infty $
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 08 January 2024, pp. 624-632
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Symmetric and antisymmetric tensor products for the function-theoretic operator theorist
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 22 December 2023, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MULTIPLIERS AND CHARACTERIZATION OF THE DUAL OF NEVANLINNA-TYPE SPACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 07 September 2023, pp. 216-240
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
Sub-Bergman Hilbert spaces on the unit disk III
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 22 August 2023, pp. 1-18
-
- Article
-
- You have access
- HTML
- Export citation
Schatten class composition operators on the Hardy space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 July 2023, pp. 1-14
-
- Article
-
- You have access
- HTML
- Export citation
Uncertainty principles in holomorphic function spaces on the unit ball
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 122-136
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Fueter-Sce mapping and the Clifford–Appell polynomials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 28 June 2023, pp. 642-688
-
- Article
-
- You have access
- HTML
- Export citation
Refined Bohr inequalities for certain classes of functions: analytic, univalent, and convex
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 09 June 2023, pp. 9-25
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
Composition operators on weighted analytic spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 17 April 2023, pp. 1213-1230
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
General Toeplitz kernels and
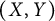 $(X,Y)$-invariance
$(X,Y)$-invariance
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 680-706
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
Constructions of some families of smooth Cauchy transforms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 26 January 2023, pp. 319-344
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

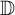
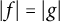
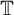
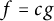
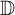
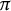
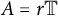






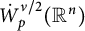
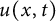
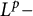
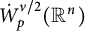
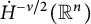
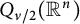
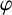
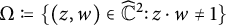 of the “complexified unit circle”
of the “complexified unit circle”