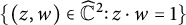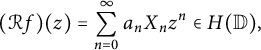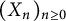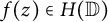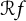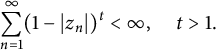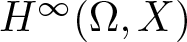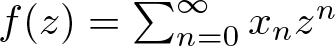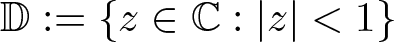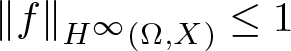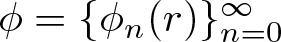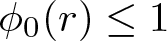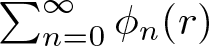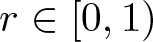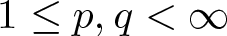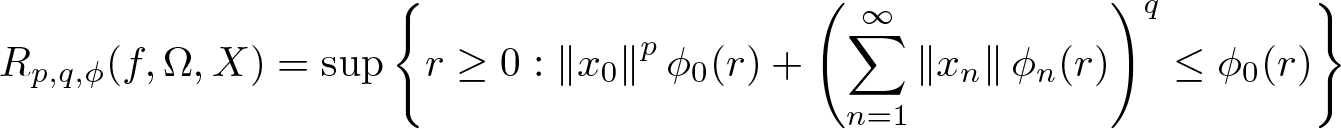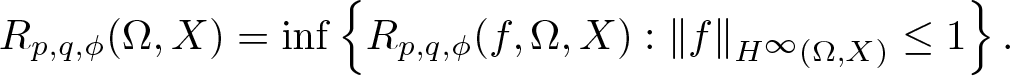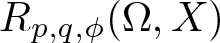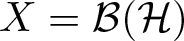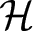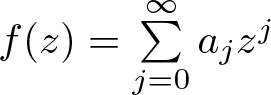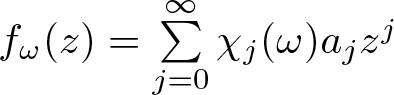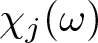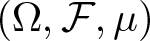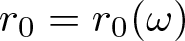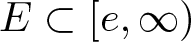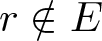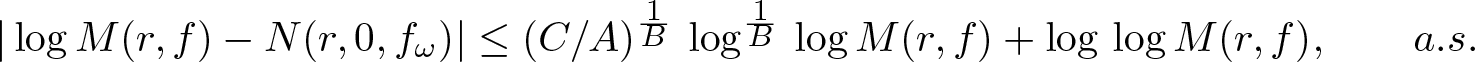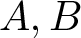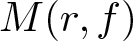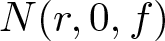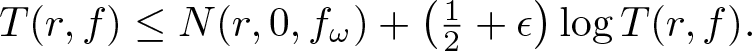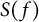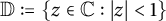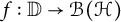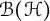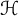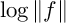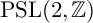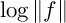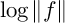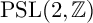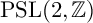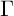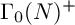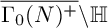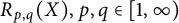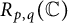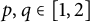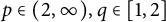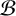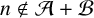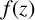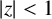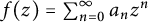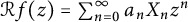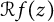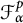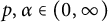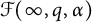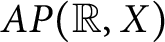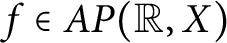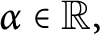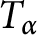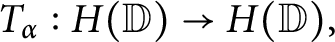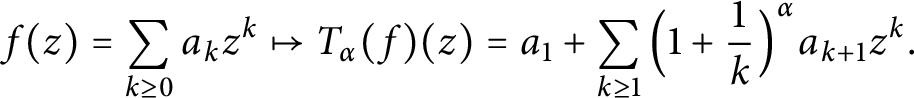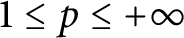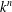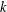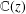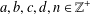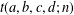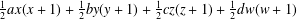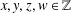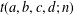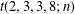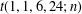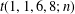40 results in 30Bxx
RADIAL ASYMPTOTICS OF GENERATING FUNCTIONS OF k-REGULAR SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-7
-
- Article
- Export citation
Solid bases and functorial constructions for (p-)Banach spaces of analytic functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 09 September 2024, pp. 1-32
-
- Article
- Export citation
Random analytic functions with a prescribed growth rate in the unit disk
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 26 April 2024, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral theory of the invariant Laplacian on the disk and the sphere – a complex analysis approach
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 01 March 2024, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A characterization of random analytic functions satisfying Blaschke-type conditions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 17 January 2024, pp. 1-10
-
- Article
- Export citation
Bohr radius for Banach spaces on simply connected domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 03 November 2023, pp. 113-141
-
- Article
- Export citation
Inequalities concerning maximum modulus and zeros of random entire functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 19 October 2023, pp. 57-78
-
- Article
- Export citation
Uncertainty principles in holomorphic function spaces on the unit ball
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 122-136
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bohr operator on operator-valued polyanalytic functions on simply connected domains
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 26 June 2023, pp. 1411-1422
- Print publication:
- December 2023
-
- Article
- Export citation
KRONECKER LIMIT FUNCTIONS AND AN EXTENSION OF THE ROHRLICH–JENSEN FORMULA
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 252 / December 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 810-841
- Print publication:
- December 2023
-
- Article
- Export citation
Estimates for generalized Bohr radii in one and higher dimensions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 04 November 2022, pp. 682-699
- Print publication:
- June 2023
-
- Article
- Export citation
A NOTE ON AN ASYMPTOTIC VERSION OF A PROBLEM OF MAHLER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 15 September 2022, pp. 398-402
- Print publication:
- June 2023
-
- Article
- Export citation
Two problems on random analytic functions in Fock spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 08 July 2022, pp. 1176-1198
- Print publication:
- August 2023
-
- Article
- Export citation
A note on spaces of almost periodic functions with values in Banach spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 18 January 2022, pp. 953-962
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unitary equivalence of multiplication operators on the Bergman spaces of polygons
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 05 March 2021, pp. 123-133
- Print publication:
- March 2022
-
- Article
- Export citation
Bohr phenomenon for operator-valued functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 72-86
-
- Article
- Export citation
Growth of frequently hypercyclic functions for some weighted Taylor shifts on the unit disc
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 11 June 2020, pp. 264-281
- Print publication:
- June 2021
-
- Article
- Export citation
VANISHING COEFFICIENTS IN QUOTIENTS OF THETA FUNCTIONS OF MODULUS FIVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 27 March 2020, pp. 387-398
- Print publication:
- December 2020
-
- Article
- Export citation
DEGREE-ONE MAHLER FUNCTIONS: ASYMPTOTICS, APPLICATIONS AND SPECULATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 05 February 2020, pp. 399-409
- Print publication:
- December 2020
-
- Article
- Export citation
TRANSFORMATION FORMULAS FOR THE NUMBER OF REPRESENTATIONS OF
 $n$ BY LINEAR COMBINATIONS OF FOUR TRIANGULAR NUMBERS
$n$ BY LINEAR COMBINATIONS OF FOUR TRIANGULAR NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 39-49
- Print publication:
- August 2020
-
- Article
- Export citation










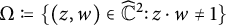 of the “complexified unit circle”
of the “complexified unit circle”