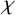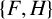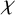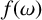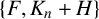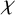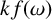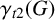922 results in 05Cxx
Cokernel statistics for walk matrices of directed and weighted random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 18 October 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Embedding theorems for random graphs with specified degrees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 16 October 2024, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
VERTEX-PRIMITIVE s-ARC-TRANSITIVE DIGRAPHS OF ALMOST SIMPLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 16 October 2024, pp. 1-2
-
- Article
-
- You have access
- HTML
- Export citation
Vertex-critical graphs far from edge-criticality
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 11 October 2024, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Approximation of subgraph counts in the uniform attachment model
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 10 October 2024, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on extremal constructions for the Erdős–Rademacher problem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 10 October 2024, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Partial recovery and weak consistency in the non-uniform hypergraph stochastic block model
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 09 October 2024, pp. 1-51
-
- Article
-
- You have access
- HTML
- Export citation
ON THE RAMSEY NUMBERS OF TREE GRAPHS VERSUS CERTAIN GENERALISED WHEEL GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 08 October 2024, pp. 1-2
-
- Article
-
- You have access
- HTML
- Export citation
The k-core in percolated dense graph sequences
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 08 October 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The game of Cops and Robber on geodesic spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 04 October 2024, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON
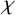 $\chi $-BINDING FUNCTIONS AND LINEAR FORESTS
$\chi $-BINDING FUNCTIONS AND LINEAR FORESTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 27 September 2024, pp. 1-7
-
- Article
-
- You have access
- HTML
- Export citation
The List-Ramsey threshold for families of graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 20 September 2024, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Domination inequalities and dominating graphs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 19 September 2024, pp. 1-18
-
- Article
-
- You have access
- HTML
- Export citation
On the Ramsey numbers of daisies I
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
SPECTRAL CLUSTERING AND LONG TIMESERIES CLASSIFICATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 18 September 2024, pp. 121-131
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Ramsey numbers of daisies II
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-27
-
- Article
-
- You have access
- HTML
- Export citation
List packing number of bounded degree graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-22
-
- Article
-
- You have access
- HTML
- Export citation
EXTREMAL GRAPHS FOR DEGREE SUMS AND DOMINATING CYCLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-7
-
- Article
-
- You have access
- HTML
- Export citation
GRAPHS WITH SEMITOTAL DOMINATION NUMBER HALF THEIR ORDER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-8
-
- Article
-
- You have access
- HTML
- Export citation
Quenched worst-case scenario for root deletion in targeted cutting of random recursive trees
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 03 September 2024, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation